R function to compute Wilcoxon test

To perform two-samples Wilcoxon test comparing the means of two independent samples (x & y), the R function wilcox.test() can be used as follow:

wilcox.test(x, y, alternative = "two.sided")

Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())
# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use an example data set, which contains the weight of 18 individuals (9 women and 9 men):

# Data in two numeric vectors
women_weight <- c(38.9, 61.2, 73.3, 21.8, 63.4, 64.6, 48.4, 48.8, 48.5)
men_weight <- c(67.8, 60, 63.4, 76, 89.4, 73.3, 67.3, 61.3, 62.4) 
# Create a data frame
my_data <- data.frame( 
                group = rep(c("Woman", "Man"), each = 9),
                weight = c(women_weight,  men_weight)
                )

We want to know, if the median women’s weight differs from the median men’s weight?

Check your data

print(my_data)

   group weight
1  Woman   38.9
2  Woman   61.2
3  Woman   73.3
4  Woman   21.8
5  Woman   63.4
6  Woman   64.6
7  Woman   48.4
8  Woman   48.8
9  Woman   48.5
10   Man   67.8
11   Man   60.0
12   Man   63.4
13   Man   76.0
14   Man   89.4
15   Man   73.3
16   Man   67.3
17   Man   61.3
18   Man   62.4

It’s possible to compute summary statistics (median and interquartile range (IQR)) by groups. The dplyr package can be used.

• To install dplyr package, type this:

install.packages("dplyr")

• Compute summary statistics by groups:

library(dplyr)
group_by(my_data, group) %>%
  summarise(
    count = n(),
    median = median(weight, na.rm = TRUE),
    IQR = IQR(weight, na.rm = TRUE)
  )

Source: local data frame [2 x 4]
   group count median   IQR
  (fctr) (int)  (dbl) (dbl)
1    Man     9   67.3  10.9
2  Woman     9   48.8  15.0

Visualize your data using box plots

You can draw R base graphs as described at this link: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization

• Install the latest version of ggpubr from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

• Visualize your data:

# Plot weight by group and color by group
library("ggpubr")
ggboxplot(my_data, x = "group", y = "weight", 
          color = "group", palette = c("#00AFBB", "#E7B800"),
          ylab = "Weight", xlab = "Groups")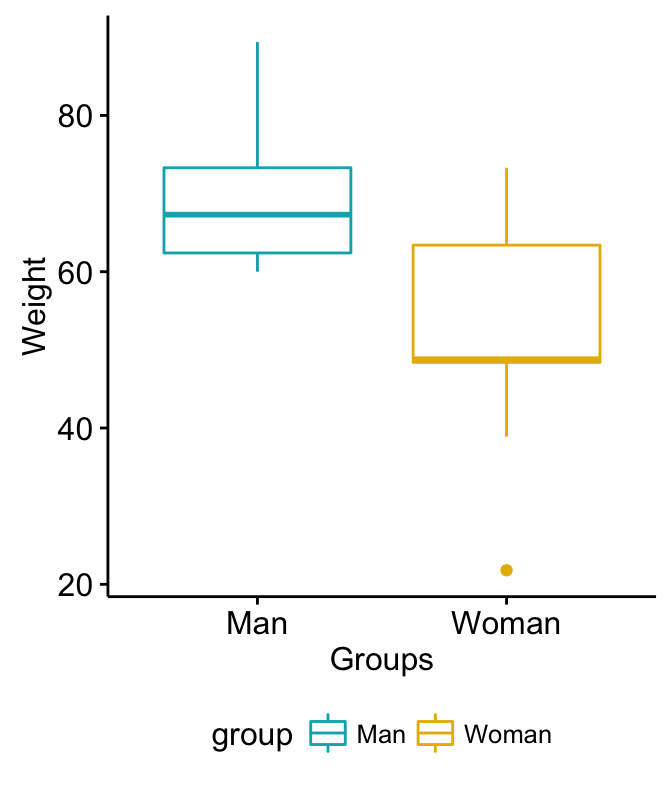

Unpaired Two-Samples Wilcoxon Test in R

Compute unpaired two-samples Wilcoxon test

Question : Is there any significant difference between women and men weights?

1) Compute two-samples Wilcoxon test - Method 1: The data are saved in two different numeric vectors.

res <- wilcox.test(women_weight, men_weight)
res

    Wilcoxon rank sum test with continuity correction
data:  women_weight and men_weight
W = 15, p-value = 0.02712
alternative hypothesis: true location shift is not equal to 0

It will give a warning message, saying that “cannot compute exact p-value with tie”. It comes from the assumption of a Wilcoxon test that the responses are continuous. You can suppress this message by adding another argument exact = FALSE, but the result will be the same.

2) Compute two-samples Wilcoxon test - Method 2: The data are saved in a data frame.

res <- wilcox.test(weight ~ group, data = my_data,
                   exact = FALSE)
res

    Wilcoxon rank sum test with continuity correction
data:  weight by group
W = 66, p-value = 0.02712
alternative hypothesis: true location shift is not equal to 0

# Print the p-value only
res$p.value

[1] 0.02711657

As you can see, the two methods give the same results.

The p-value of the test is 0.02712, which is less than the significance level alpha = 0.05. We can conclude that men’s median weight is significantly different from women’s median weight with a p-value = 0.02712.

wilcox.test(weight ~ group, data = my_data, 
        exact = FALSE, alternative = "less")

wilcox.test(weight ~ group, data = my_data,
        exact = FALSE, alternative = "greater")