Normality Test in R


Many of statistical tests including correlation, regression, t-test, and analysis of variance (ANOVA) assume some certain characteristics about the data. They require the data to follow a normal distribution or Gaussian distribution. These tests are called parametric tests, because their validity depends on the distribution of the data.

Normality and the other assumptions made by these tests should be taken seriously to draw reliable interpretation and conclusions of the research.

Before using a parametric test, we should perform some preleminary tests to make sure that the test assumptions are met. In the situations where the assumptions are violated, non-paramatric tests are recommended.

Here, we’ll describe how to check the normality of the data by visual inspection and by significance tests.


Related Book:


Practical Statistics in R for Comparing Groups: Numerical Variables

Install required R packages

  1. dplyr for data manipulation
install.packages("dplyr")
  1. ggpubr for an easy ggplot2-based data visualization
  • Install the latest version from GitHub as follow:
# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")
  • Or, install from CRAN as follow:
install.packages("ggpubr")

Load required R packages

library("dplyr")
library("ggpubr")

Import your data into R

  1. Prepare your data as specified here: Best practices for preparing your data set for R

  2. Save your data in an external .txt tab or .csv files

  3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())
# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use the built-in R data set named ToothGrowth.

# Store the data in the variable my_data
my_data <- ToothGrowth

Check your data

We start by displaying a random sample of 10 rows using the function sample_n()[in dplyr package].

Show 10 random rows:

set.seed(1234)
dplyr::sample_n(my_data, 10)
    len supp dose
7  11.2   VC  0.5
37  8.2   OJ  0.5
36 10.0   OJ  0.5
58 27.3   OJ  2.0
49 14.5   OJ  1.0
57 26.4   OJ  2.0
1   4.2   VC  0.5
13 15.2   VC  1.0
35 14.5   OJ  0.5
27 26.7   VC  2.0

Assess the normality of the data in R

We want to test if the variable len (tooth length) is normally distributed.

Case of large sample sizes

If the sample size is large enough (n > 30), we can ignore the distribution of the data and use parametric tests.

The central limit theorem tells us that no matter what distribution things have, the sampling distribution tends to be normal if the sample is large enough (n > 30).

However, to be consistent, normality can be checked by visual inspection [normal plots (histogram), Q-Q plot (quantile-quantile plot)] or by significance tests].

Visual methods

Density plot and Q-Q plot can be used to check normality visually.

  1. Density plot: the density plot provides a visual judgment about whether the distribution is bell shaped.
library("ggpubr")
ggdensity(my_data$len, 
          main = "Density plot of tooth length",
          xlab = "Tooth length")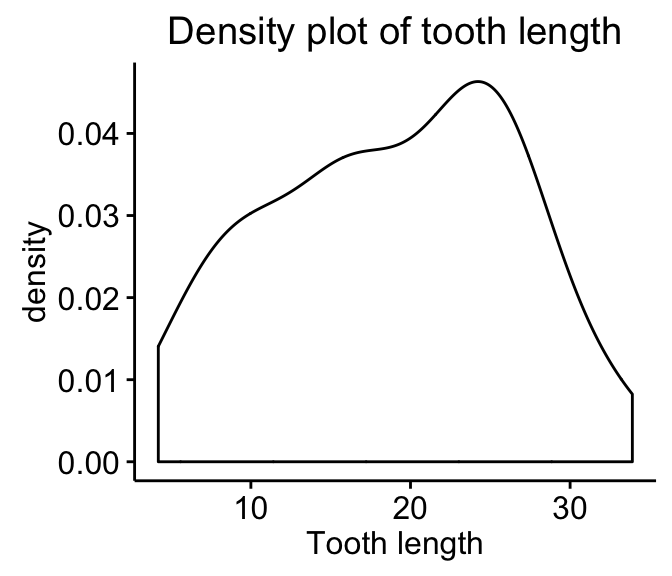

  1. Q-Q plot: Q-Q plot (or quantile-quantile plot) draws the correlation between a given sample and the normal distribution. A 45-degree reference line is also plotted.
library(ggpubr)
ggqqplot(my_data$len)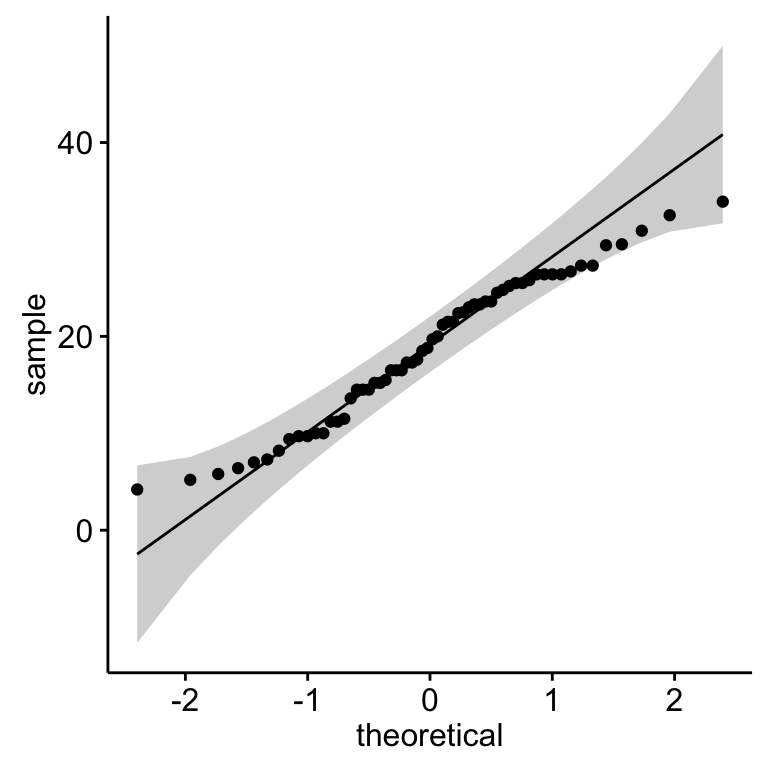

It’s also possible to use the function qqPlot() [in car package]:

library("car")
qqPlot(my_data$len)

As all the points fall approximately along this reference line, we can assume normality.

Normality test

Visual inspection, described in the previous section, is usually unreliable. It’s possible to use a significance test comparing the sample distribution to a normal one in order to ascertain whether data show or not a serious deviation from normality.

There are several methods for normality test such as Kolmogorov-Smirnov (K-S) normality test and Shapiro-Wilk’s test.

The null hypothesis of these tests is that “sample distribution is normal”. If the test is significant, the distribution is non-normal.

Shapiro-Wilk’s method is widely recommended for normality test and it provides better power than K-S. It is based on the correlation between the data and the corresponding normal scores.

Note that, normality test is sensitive to sample size. Small samples most often pass normality tests. Therefore, it’s important to combine visual inspection and significance test in order to take the right decision.

The R function shapiro.test() can be used to perform the Shapiro-Wilk test of normality for one variable (univariate):

shapiro.test(my_data$len)

    Shapiro-Wilk normality test
data:  my_data$len
W = 0.96743, p-value = 0.1091

From the output, the p-value > 0.05 implying that the distribution of the data are not significantly different from normal distribution. In other words, we can assume the normality.

Infos

This analysis has been performed using R software (ver. 3.2.4).


Enjoyed this article? I’d be very grateful if you’d help it spread by emailing it to a friend, or sharing it on Twitter, Facebook or Linked In.

Show me some love with the like buttons below... Thank you and please don't forget to share and comment below!!
Avez vous aimé cet article? Je vous serais très reconnaissant si vous aidiez à sa diffusion en l'envoyant par courriel à un ami ou en le partageant sur Twitter, Facebook ou Linked In.

Montrez-moi un peu d'amour avec les like ci-dessous ... Merci et n'oubliez pas, s'il vous plaît, de partager et de commenter ci-dessous!





This page has been seen 1217519 times