FactoMineR and factoextra : Principal Component Analysis Visualization - R software and data mining

This article has been updated, you are now consulting an old release of this article!


Principal component analysis (PCA) allows us to summarize the variations (informations) in a data set described by multiple variables. Each variable could be considered as a different dimension. If you have more than 3 variables in your data sets, it could be very difficult to visualize a multi-dimensional hyperspace.

The goal of principal component analysis is to transform the initial variables into a new set of variables which explain the variation in the data. These new variables corresponds to a linear combination of the originals and are called principal components.

PCA reduces the dimensionality of multivariate data, to two or three that can be visualized graphically with minimal loss of information.

Several functions from different packages are available in R for performing PCA : prcomp and princomp (built-in R stats package), PCA (FactoMineR package), dudi.pca(ade4 package).


This R tutorial describes :

  1. How to perform a principal component analysis using R software and FactoMineR package
  2. How to visualize the output of the PCA using the R package factoextra


Install and load FactoMineR package

FactoMineR (Husson et al.) is one of the most powerful R packages and my favorite one for performing a multivariate exploratory data analysis. A rich documentation is available on the FactoMineR official website (http://factominer.free.fr/index.html) and on youtube. Many thanks to François Husson for this effort…

FactoMineR can be installed and loaded as follow :

install.packages("FactoMineR")
library("FactoMineR")

Install and load factoextra for visualization

The package factoextra has flexible methods for the classes PCA, prcomp, princomp and dudi in order to extract and visualize quickly the results of the analysis. The ggplot2 plotting system is used for the data visualization.

Install and load factoextra as follow :

library("devtools")
install_github("kassambara/factoextra")

Load it :

library("factoextra")

Prepare the data

We’ll used the data sets decathlon2 from the package factoextra :

data(decathlon2)
head(decathlon2[, 1:6])
           X100m Long.jump Shot.put High.jump X400m X110m.hurdle
SEBRLE     11.04      7.58    14.83      2.07 49.81        14.69
CLAY       10.76      7.40    14.26      1.86 49.37        14.05
BERNARD    11.02      7.23    14.25      1.92 48.93        14.99
YURKOV     11.34      7.09    15.19      2.10 50.42        15.31
ZSIVOCZKY  11.13      7.30    13.48      2.01 48.62        14.17
McMULLEN   10.83      7.31    13.76      2.13 49.91        14.38

This data is just a subset of the decathlon data in FactoMineR package

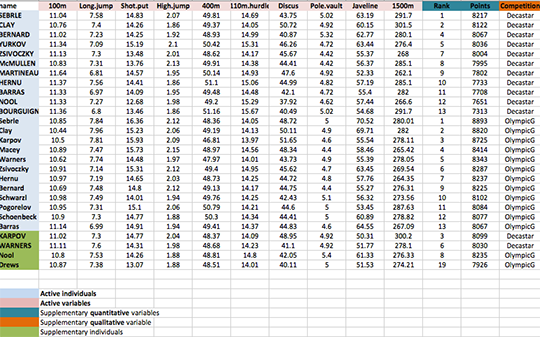
As illustrated below, the data used here describes athletes’ performance during two sporting events (Desctar and OlympicG). It contains 27 individuals (athletes) described by 13 variables :

principal component analysis data


Only some of these individuals and variables will be used to perform the principal component analysis (PCA).

The coordinates of the remaining individuals and variables on the factor map will be predicted after the PCA.


In PCA terminology, our data contains :


  • Active individuals (in blue, rows 1:23) : Individuals that are used during the principal component analysis.
  • Supplementary individuals (in green, rows 24:27) : The coordinates of these individuals will be predicted using the PCA informations and parameters obtained with active individuals/variables
  • Active variables (in pink, columns 1:10) : Variables that are used for the principal component analysis.
  • Supplementary variables : As supplementary individuals, the coordinates of these variables will be predicted also.
  • Supplementary continuous variables : Columns 11 and 12 corresponding respectively to the rank and the points of athletes.
  • Supplementary qualitative variables : Column 13 corresponding to the two athlete-tic meetings (2004 Olympic Game or 2004 Decastar). This factor variables will be used to color individuals by groups.


Extract only active individuals and variables for principal component analysis:

decathlon2.active <- decathlon2[1:23, 1:10]
head(decathlon2.active[, 1:6])
           X100m Long.jump Shot.put High.jump X400m X110m.hurdle
SEBRLE     11.04      7.58    14.83      2.07 49.81        14.69
CLAY       10.76      7.40    14.26      1.86 49.37        14.05
BERNARD    11.02      7.23    14.25      1.92 48.93        14.99
YURKOV     11.34      7.09    15.19      2.10 50.42        15.31
ZSIVOCZKY  11.13      7.30    13.48      2.01 48.62        14.17
McMULLEN   10.83      7.31    13.76      2.13 49.91        14.38

Exploratory data analysis

Before principal component analysis, we can perform some exploratory data analysis such as descriptive statistics, correlation matrix and scatter plot matrix.

Descriptive statistics

decathlon2.active_stats <- data.frame(
  Min = apply(decathlon2.active, 2, min), # minimum
  Q1 = apply(decathlon2.active, 2, quantile, 1/4), # First quartile
  Med = apply(decathlon2.active, 2, median), # median
  Mean = apply(decathlon2.active, 2, mean), # mean
  Q3 = apply(decathlon2.active, 2, quantile, 3/4), # Third quartile
  Max = apply(decathlon2.active, 2, max) # Maximum
  )
decathlon2.active_stats <- round(decathlon2.active_stats, 1)
head(decathlon2.active_stats)
              Min   Q1  Med Mean   Q3  Max
X100m        10.4 10.8 11.0 11.0 11.2 11.6
Long.jump     6.8  7.2  7.3  7.3  7.5  8.0
Shot.put     12.7 14.2 14.7 14.6 15.1 16.4
High.jump     1.9  1.9  2.0  2.0  2.1  2.1
X400m        46.8 49.0 49.4 49.4 50.0 51.2
X110m.hurdle 14.0 14.2 14.4 14.5 14.9 15.7

Note that, you can also use the built-in R function summary() for the descriptive statistics but I don’t like the format of the output on data frame.

Correlation matrix

The correlation between variables can be calculated as follow :

cor.mat <- round(cor(decathlon2.active),2)
head(cor.mat[, 1:6])
             X100m Long.jump Shot.put High.jump X400m X110m.hurdle
X100m         1.00     -0.76    -0.45     -0.40  0.59         0.73
Long.jump    -0.76      1.00     0.44      0.34 -0.51        -0.59
Shot.put     -0.45      0.44     1.00      0.53 -0.31        -0.38
High.jump    -0.40      0.34     0.53      1.00 -0.37        -0.25
X400m         0.59     -0.51    -0.31     -0.37  1.00         0.58
X110m.hurdle  0.73     -0.59    -0.38     -0.25  0.58         1.00

Visualize the correlation matrix using a correlogram : the package corrplot is required.

# install.packages("corrplot")
library("corrplot")
corrplot(cor.mat, type="upper", order="hclust", 
         tl.col="black", tl.srt=45)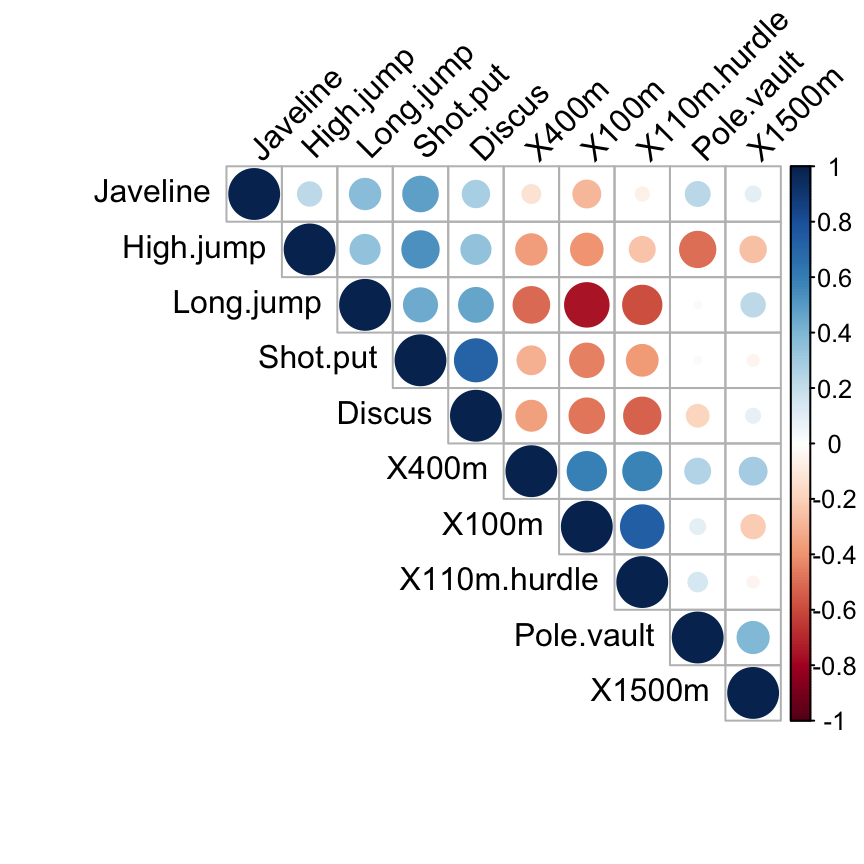

FactoMineR and factoextra : Principal component analysis - R software and data mining

Read more about visualizing correlation matrix : Correlation matrix visualization

Make a scatter plot matrix showing the correlation coefficients between variables and the significance levels : the package PerformanceAnalytics is required.

# install.packages("PerformanceAnalytics")
library("PerformanceAnalytics")
chart.Correlation(decathlon2.active[, 1:6], histogram=TRUE, pch=19)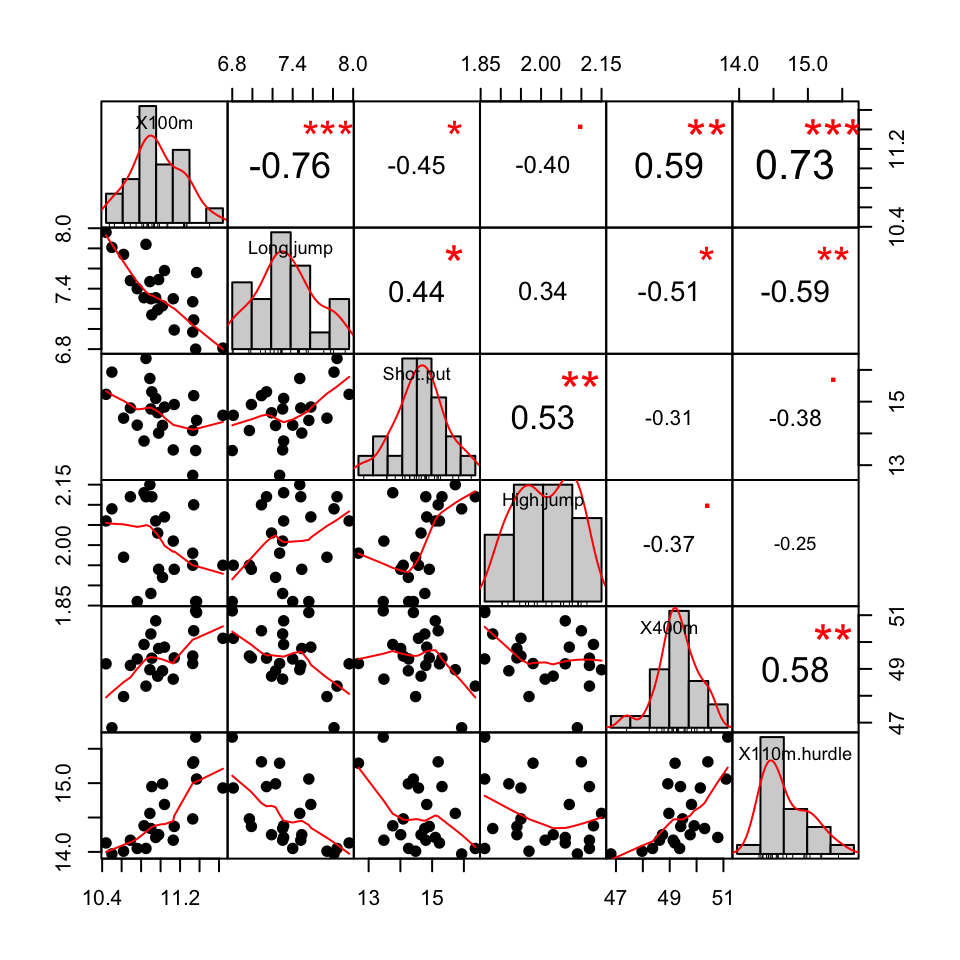

FactoMineR and factoextra : Principal component analysis - R software and data mining

You can read more about this plot here : Correlation matrix visualization

Principal component analysis

The function PCA() [in FactoMiner package] can be used. A simplified format is :

PCA(X, scale.unit = TRUE, ncp = 5, graph = TRUE)

  • X : a data frame. Rows are individuals and columns are numeric variables
  • scale.unit : a logical value. If TRUE, the data are scaled to unit variance before the analysis. This standardization to the same scale avoids some variables to become dominant just because of their large measurement units.
  • ncp : number of dimensions kept in the final results.
  • graph : a logical value. If TRUE a graph is displayed.


In the R code below, the PCA is performed only on the active individuals/variables :

library("FactoMineR")
res.pca <- PCA(decathlon2.active, graph = FALSE)

The output of the function PCA() is a list including :

print(res.pca)
**Results for the Principal Component Analysis (PCA)**
The analysis was performed on 23 individuals, described by 10 variables
*The results are available in the following objects:
   name               description                          
1  "$eig"             "eigenvalues"                        
2  "$var"             "results for the variables"          
3  "$var$coord"       "coord. for the variables"           
4  "$var$cor"         "correlations variables - dimensions"
5  "$var$cos2"        "cos2 for the variables"             
6  "$var$contrib"     "contributions of the variables"     
7  "$ind"             "results for the individuals"        
8  "$ind$coord"       "coord. for the individuals"         
9  "$ind$cos2"        "cos2 for the individuals"           
10 "$ind$contrib"     "contributions of the individuals"   
11 "$call"            "summary statistics"                 
12 "$call$centre"     "mean of the variables"              
13 "$call$ecart.type" "standard error of the variables"    
14 "$call$row.w"      "weights for the individuals"        
15 "$call$col.w"      "weights for the variables"

The object that is created using the function PCA() contains many informations found in many different lists and matrices. These values are described in the next section.

Variances of the principal components

The proportion of variances retained by the principal components can be extracted as follow :

eigenvalues <- res.pca$eig
head(eigenvalues[, 1:2])
       eigenvalue percentage of variance
comp 1  4.1242133              41.242133
comp 2  1.8385309              18.385309
comp 3  1.2391403              12.391403
comp 4  0.8194402               8.194402
comp 5  0.7015528               7.015528
comp 6  0.4228828               4.228828

  • Eigenvalues correspond to the amount of the variation explained by each principal component (PC). Eigenvalues are large for the first PC and small for the subsequent PCs.

  • A PC with an eigenvalue > 1 indicates that the PC accounts for more variance than accounted by one of the original variables in standardized data. This is commonly used as a cutoff point to determine the number of PCs to retain.

Make a scree plot using base graphics : A scree plot is a graph of the eigenvalues/variances associated with components.

barplot(eigenvalues[, 2], names.arg=1:nrow(eigenvalues), 
       main = "Variances",
       xlab = "Principal Components",
       ylab = "Percentage of variances",
       col ="steelblue")
# Add connected line segments to the plot
lines(x = 1:nrow(eigenvalues), eigenvalues[, 2], 
      type="b", pch=19, col = "red")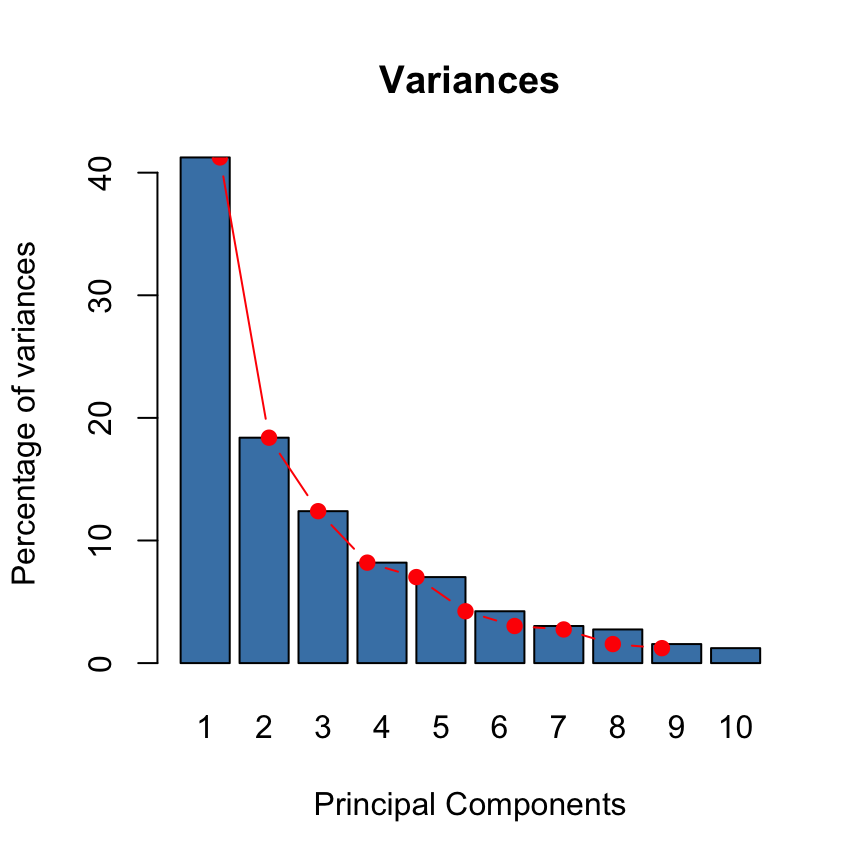

FactoMineR and factoextra : Principal component analysis - R software and data mining

~60% of the informations (variances) contained in the data are retained by the first two principal components.

Make the scree plot using the package factoextra :

fviz_screeplot(res.pca, ncp=10)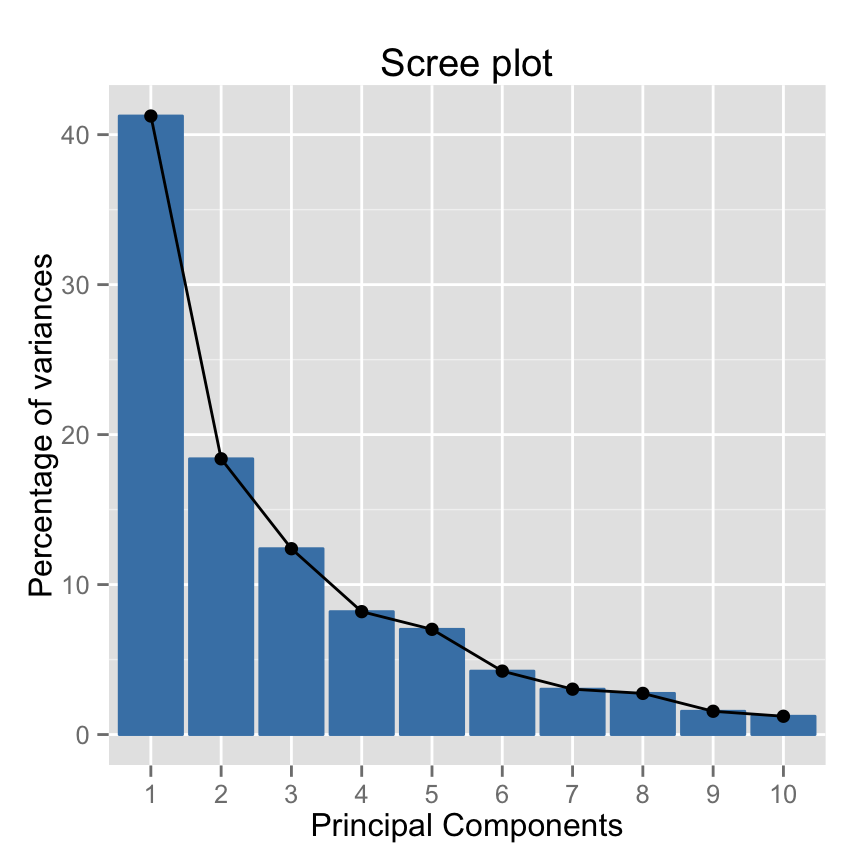

FactoMineR and factoextra : Principal component analysis - R software and data mining

Graph of individus and variables

The function plot.PCA() can be used. A simplified format is :

plot.PCA(x, axes = c(1,2), choix=c("ind", "var"))

  • x : An object of class PCA
  • axes : A numeric vector of length 2 specifying the component to plot
  • choix : The graph to be plotted. Possible values are “ind” for the individuals and “var” for the variables


Variables factor map : The correlation circle

Coordinates of variables on the principal components

head(res.pca$var$coord)
                  Dim.1       Dim.2      Dim.3       Dim.4      Dim.5
X100m        -0.8506257 -0.17939806  0.3015564  0.03357320 -0.1944440
Long.jump     0.7941806  0.28085695 -0.1905465 -0.11538956  0.2331567
Shot.put      0.7339127  0.08540412  0.5175978  0.12846837 -0.2488129
High.jump     0.6100840 -0.46521415  0.3300852  0.14455012  0.4027002
X400m        -0.7016034  0.29017826  0.2835329  0.43082552  0.1039085
X110m.hurdle -0.7641252 -0.02474081  0.4488873 -0.01689589  0.2242200

Cos2 : quality of variables on the factor map

The quality of representation of the variables of the principal components are called the cos2.

head(res.pca$var$cos2)
                 Dim.1        Dim.2      Dim.3        Dim.4      Dim.5
X100m        0.7235641 0.0321836641 0.09093628 0.0011271597 0.03780845
Long.jump    0.6307229 0.0788806285 0.03630798 0.0133147506 0.05436203
Shot.put     0.5386279 0.0072938636 0.26790749 0.0165041211 0.06190783
High.jump    0.3722025 0.2164242070 0.10895622 0.0208947375 0.16216747
X400m        0.4922473 0.0842034209 0.08039091 0.1856106269 0.01079698
X110m.hurdle 0.5838873 0.0006121077 0.20149984 0.0002854712 0.05027463

Contributions of the variables to the principal components

Variable contributions in the determination of a given principal component are (in percentage) : (var.cos2 * 100) / (total cos2 of the component)

head(res.pca$var$contrib)
                 Dim.1      Dim.2     Dim.3       Dim.4     Dim.5
X100m        17.544293  1.7505098  7.338659  0.13755240  5.389252
Long.jump    15.293168  4.2904162  2.930094  1.62485936  7.748815
Shot.put     13.060137  0.3967224 21.620432  2.01407269  8.824401
High.jump     9.024811 11.7715838  8.792888  2.54987951 23.115504
X400m        11.935544  4.5799296  6.487636 22.65090599  1.539012
X110m.hurdle 14.157544  0.0332933 16.261261  0.03483735  7.166193

Graph of variables using FactoMineR base graph

plot(res.pca, choix = "var")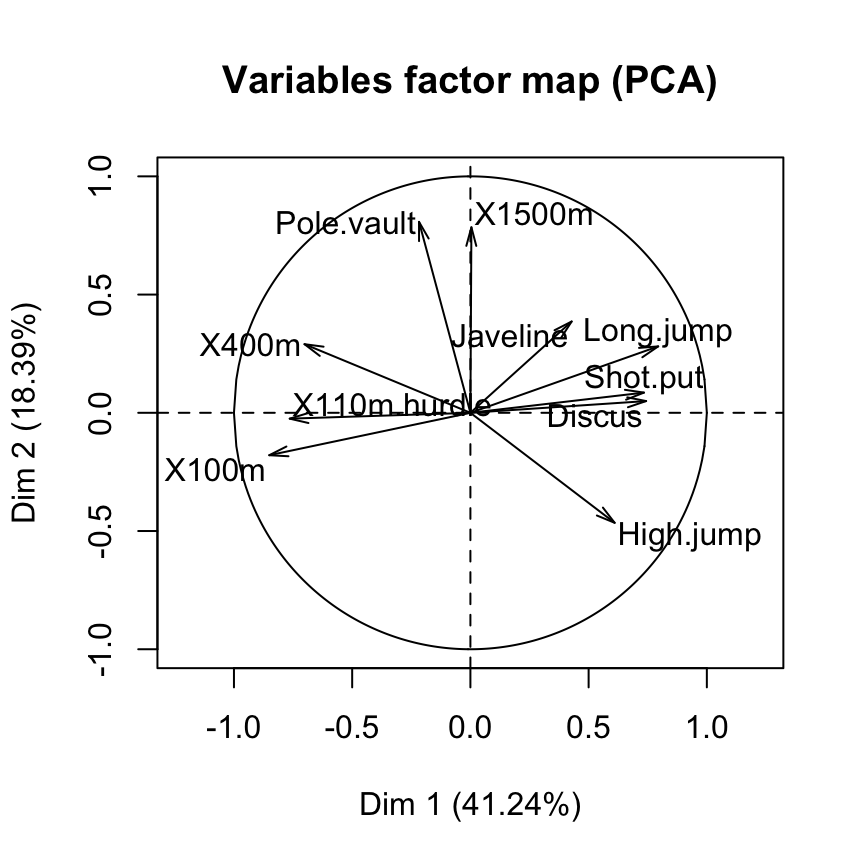

FactoMineR and factoextra : Principal component analysis - R software and data mining

Graph of variables using factoextra

The function fviz_pca_var() is used to visualize variables :

# Default plot
fviz_pca_var(res.pca)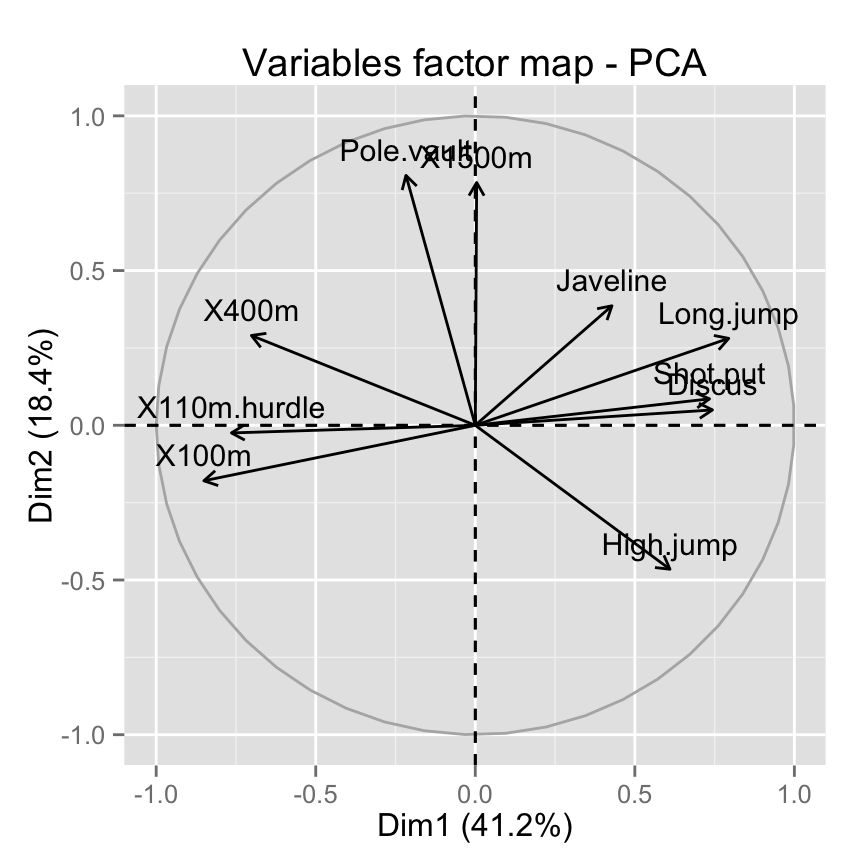

FactoMineR and factoextra : Principal component analysis - R software and data mining

# Change color and theme
fviz_pca_var(res.pca, col.var="steelblue")+
  theme_minimal()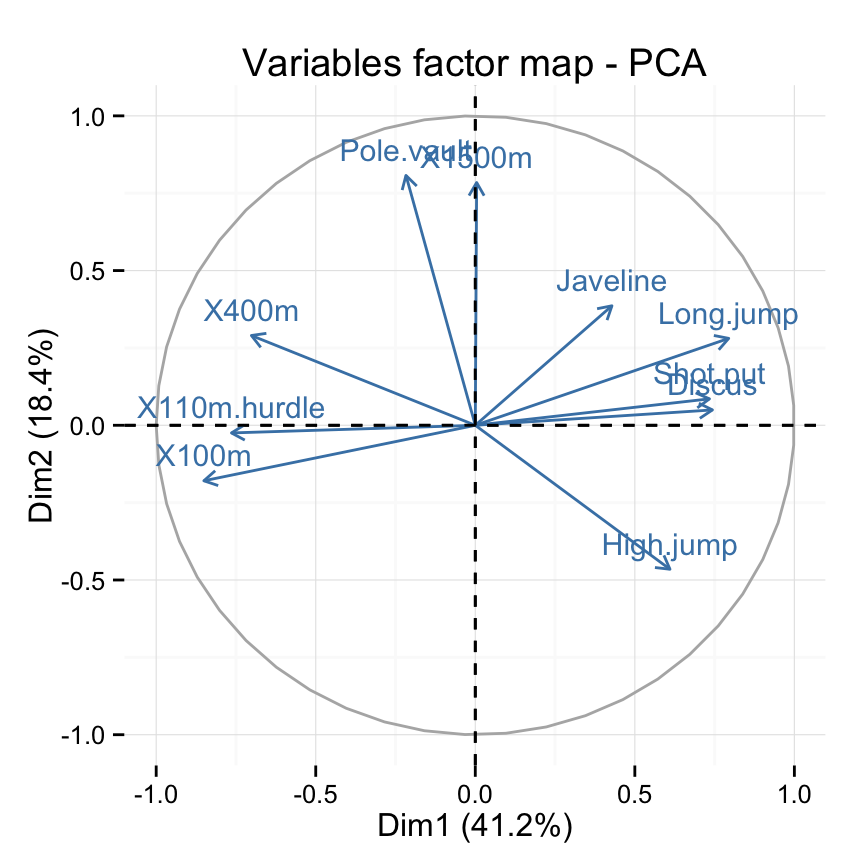

FactoMineR and factoextra : Principal component analysis - R software and data mining

Note that, using factoextra package, the color or the transparency of variables can be automatically controlled by the value of their contributions, their cos2, their coordinates on x or y axis.

# Control variable colors using their contribution
# Possible values for the argument col.var are :
  # "cos2", "contrib", "coord", "x", "y"
fviz_pca_var(res.pca, col.var="contrib")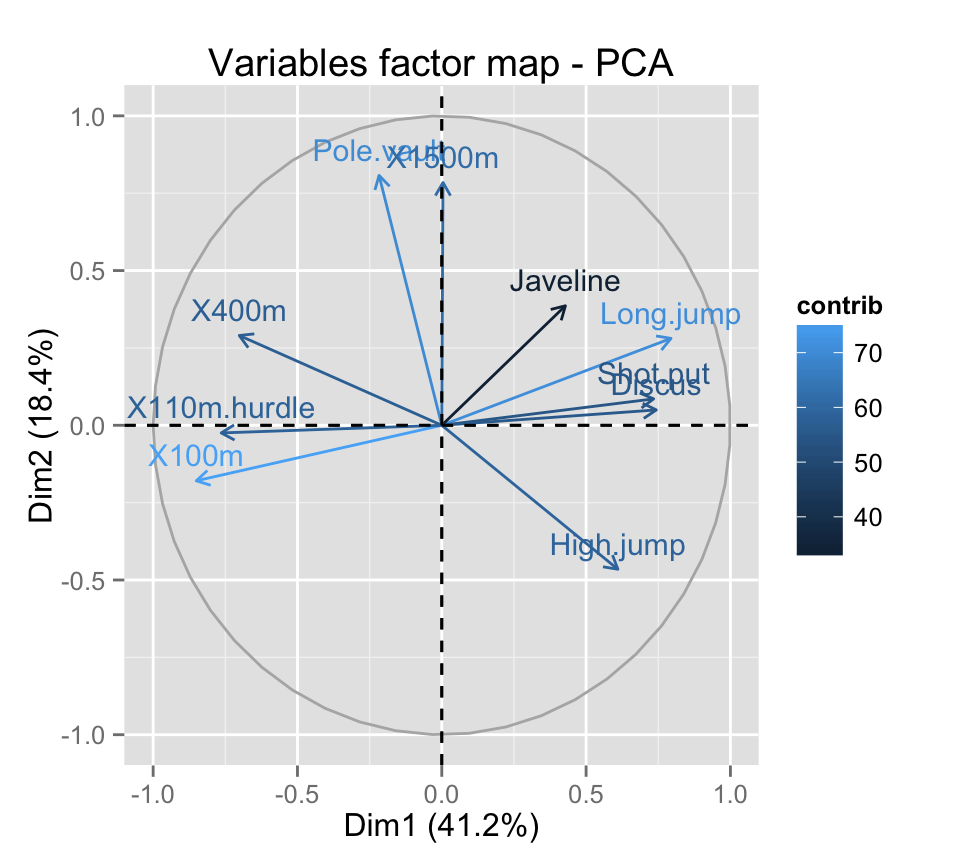

FactoMineR and factoextra : Principal component analysis - R software and data mining

# Change the gradient color
fviz_pca_var(res.pca, col.var="contrib")+
scale_color_gradient2(low="blue", mid="white", 
                      high="red", midpoint=55)+theme_bw()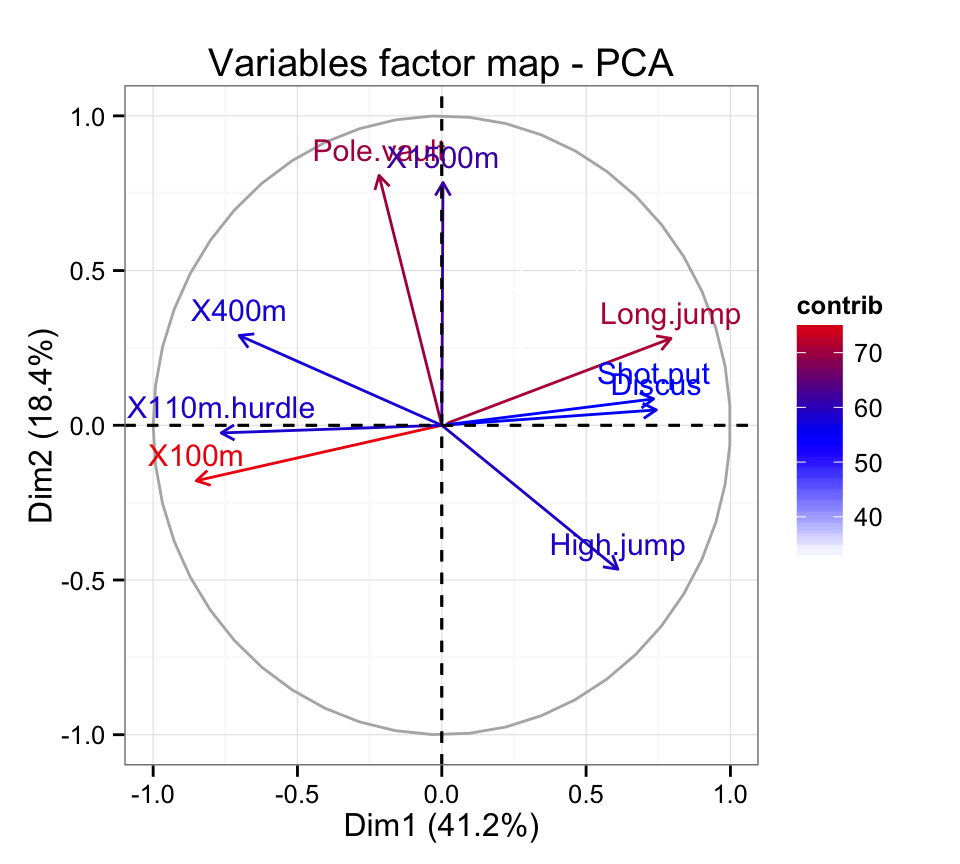

FactoMineR and factoextra : Principal component analysis - R software and data mining

This is helpful to highlight the most important variables in the determination of the principal components.

It’s also possible to control automatically the transparency of variables by their contributions :

# Control the transparency of variables using their contribution
# Possible values for the argument alpha.var are :
  # "cos2", "contrib", "coord", "x", "y"
fviz_pca_var(res.pca, alpha.var="contrib")+
  theme_minimal()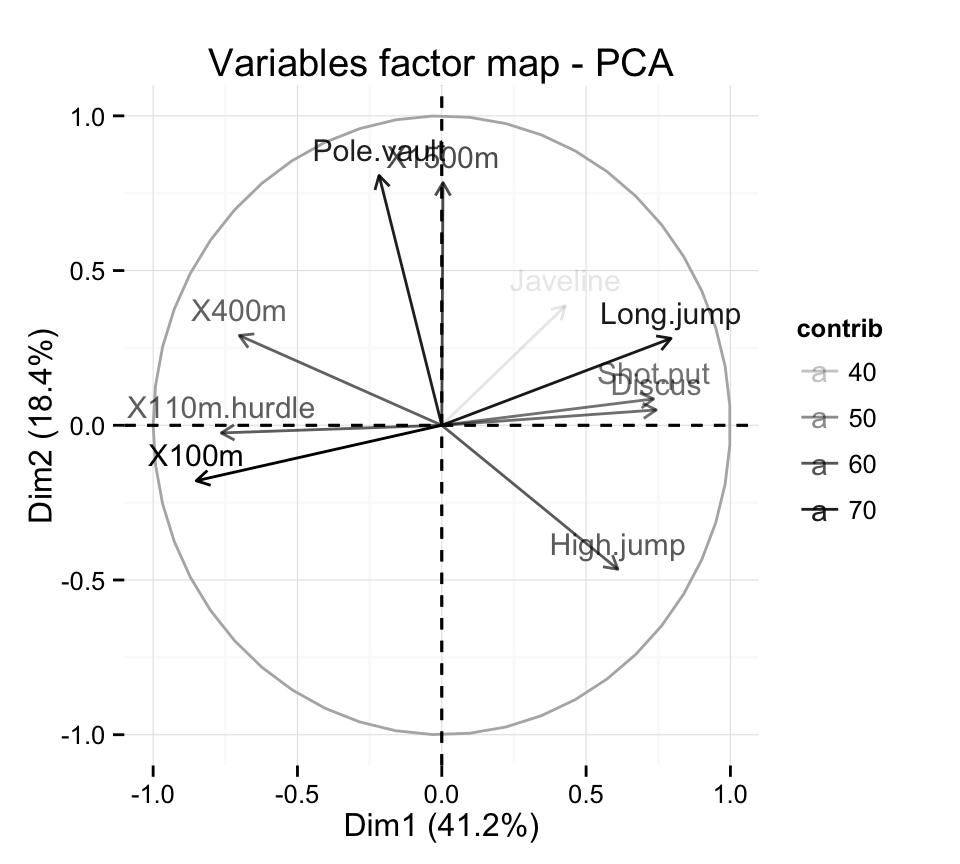

FactoMineR and factoextra : Principal component analysis - R software and data mining

Read more about ggplot2 and colors here : ggplot2 colors - How to change colors automatically and manually?

Graph of individuals

Coordinates of individuals on the principal components

head(res.pca$ind$coord)
                Dim.1      Dim.2      Dim.3       Dim.4       Dim.5
SEBRLE      0.1955047  1.5890567  0.6424912  0.08389652  1.16829387
CLAY        0.8078795  2.4748137 -1.3873827  1.29838232 -0.82498206
BERNARD    -1.3591340  1.6480950  0.2005584 -1.96409420  0.08419345
YURKOV     -0.8889532 -0.4426067  2.5295843  0.71290837  0.40782264
ZSIVOCZKY  -0.1081216 -2.0688377 -1.3342591 -0.10152796 -0.20145217
McMULLEN    0.1212195 -1.0139102 -0.8625170  1.34164291  1.62151286

Cos2 : quality of representation of individuals on the principal components

head(res.pca$ind$cos2)
                 Dim.1      Dim.2       Dim.3       Dim.4        Dim.5
SEBRLE     0.007530179 0.49747323 0.081325232 0.001386688 0.2689026575
CLAY       0.048701249 0.45701660 0.143628117 0.125791741 0.0507850580
BERNARD    0.197199804 0.28996555 0.004294015 0.411819183 0.0007567259
YURKOV     0.096109800 0.02382571 0.778230322 0.061812637 0.0202279796
ZSIVOCZKY  0.001574385 0.57641944 0.239754152 0.001388216 0.0054654972
McMULLEN   0.002175437 0.15219499 0.110137872 0.266486530 0.3892621478

Contribition of individuals to the princial components

head(res.pca$ind$contrib)
                Dim.1      Dim.2      Dim.3       Dim.4       Dim.5
SEBRLE     0.04029447  5.9714533  1.4483919  0.03734589  8.45894063
CLAY       0.68805664 14.4839248  6.7537381  8.94458283  4.21794385
BERNARD    1.94740183  6.4234107  0.1411345 20.46819433  0.04393073
YURKOV     0.83308415  0.4632733 22.4517396  2.69663605  1.03075263
ZSIVOCZKY  0.01232413 10.1217143  6.2464325  0.05469230  0.25151025
McMULLEN   0.01549089  2.4310854  2.6102794  9.55055888 16.29493304

Graph of individuals using FactoMineR base graph

plot(res.pca, choix = "ind")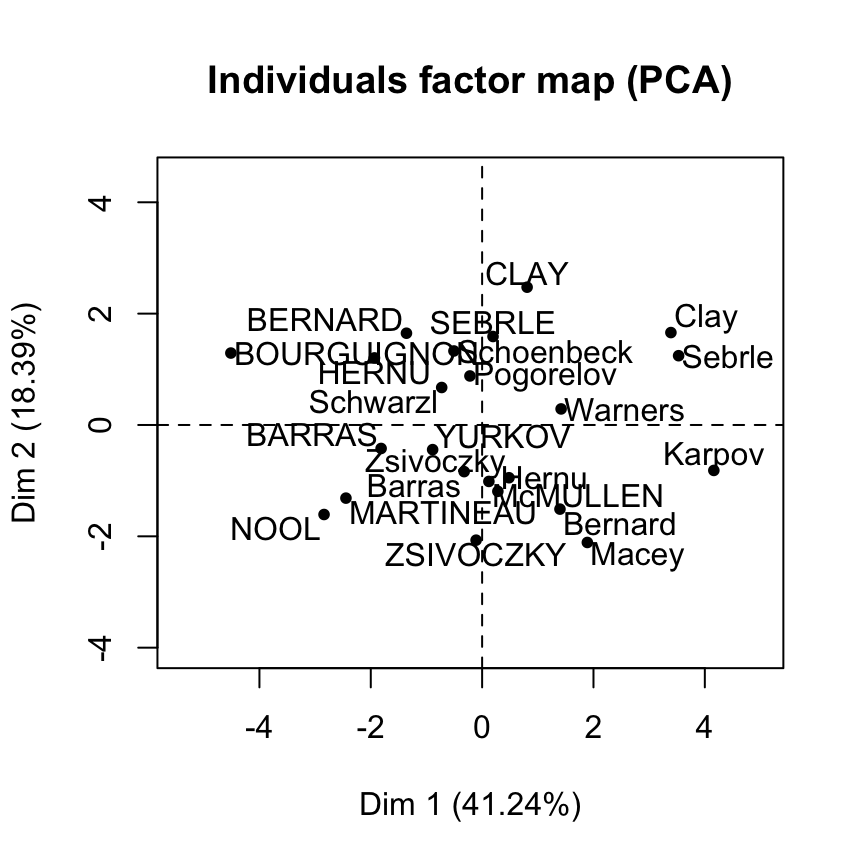

FactoMineR and factoextra : Principal component analysis - R software and data mining

Graph of individuals using factoextra

The function fviz_pca_ind() is used to visualize individuals :

fviz_pca_ind(res.pca)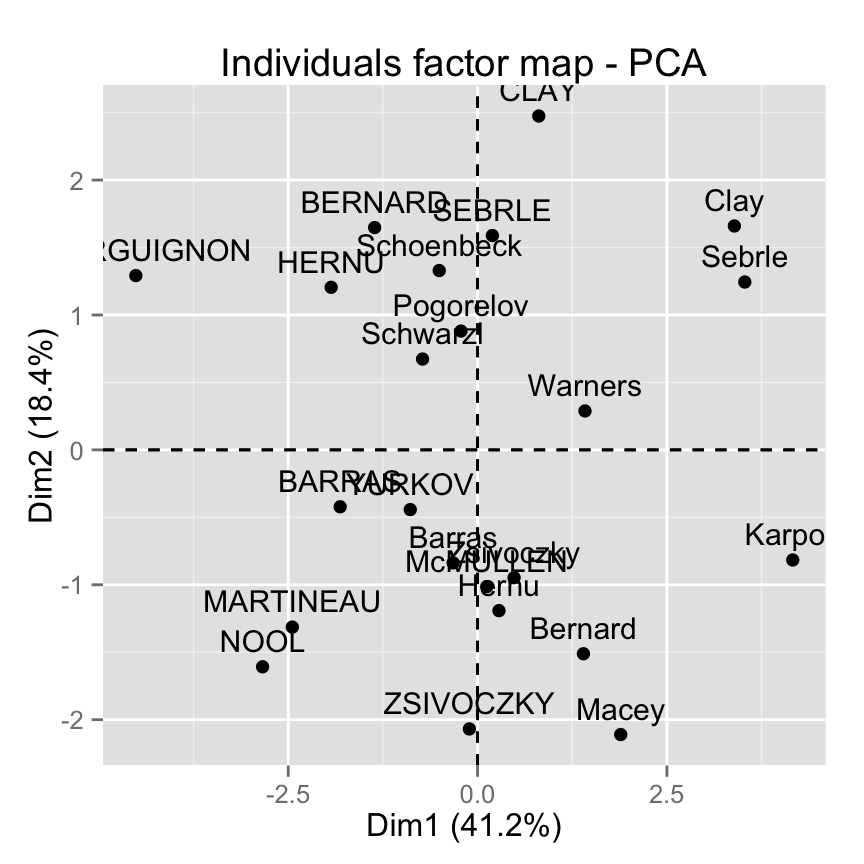

FactoMineR and factoextra : Principal component analysis - R software and data mining

Remove the points from the graph, use texts only :

fviz_pca_ind(res.pca, geom="text")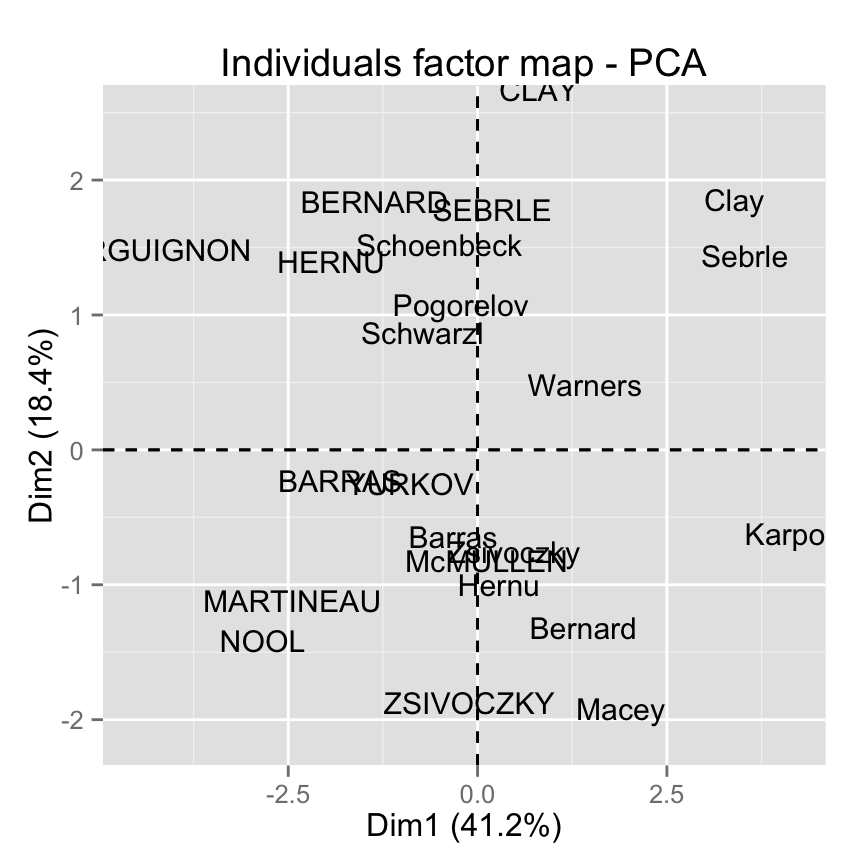

FactoMineR and factoextra : Principal component analysis - R software and data mining


Note that, allowed values for the argument geom are :

  • “point” to show only points (dots)
  • “text” to show only labels
  • c(“point”, “text”) to show both types


Control automatically the color of individuals using the cos2 values (the quality of the individuals on the factor map) :

fviz_pca_ind(res.pca, col.ind="cos2") +
scale_color_gradient2(low="blue", mid="white", 
                      high="red", midpoint=0.50)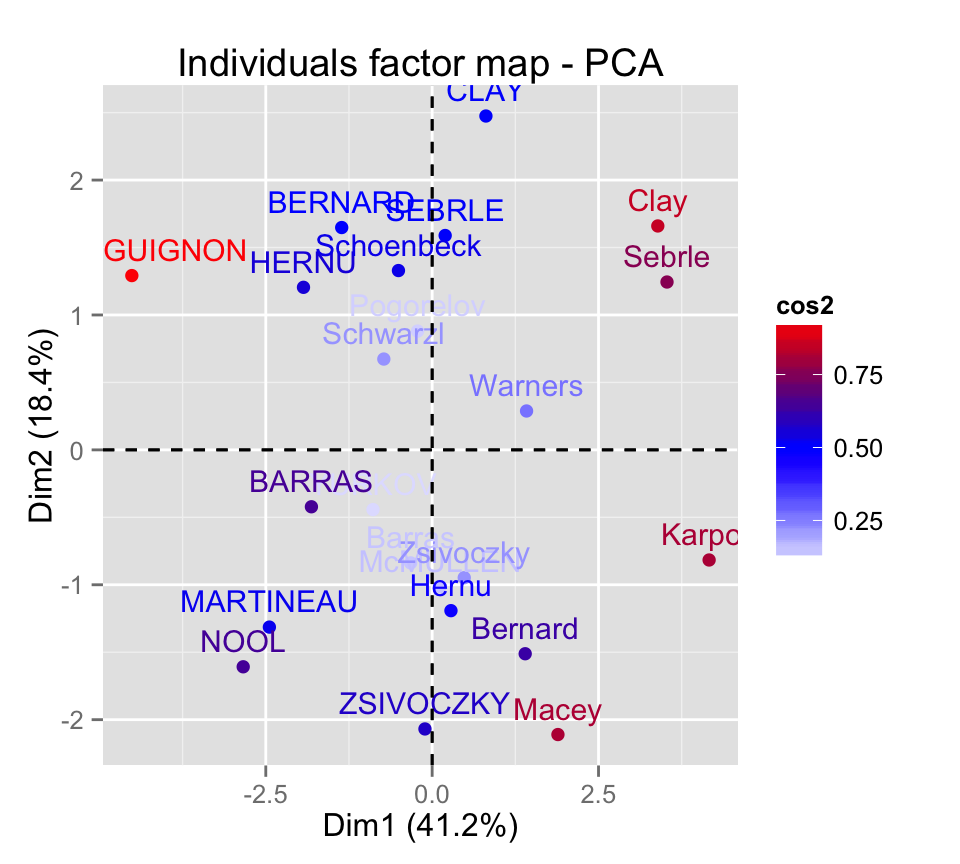

FactoMineR and factoextra : Principal component analysis - R software and data mining

Read more about ggplot2 and colors here : ggplot2 colors - How to change colors automatically and manually?

Change the theme :

fviz_pca_ind(res.pca,  col.ind="cos2") +
scale_color_gradient2(low="blue", mid="white", 
                      high="red", midpoint=0.50)+
  theme_minimal()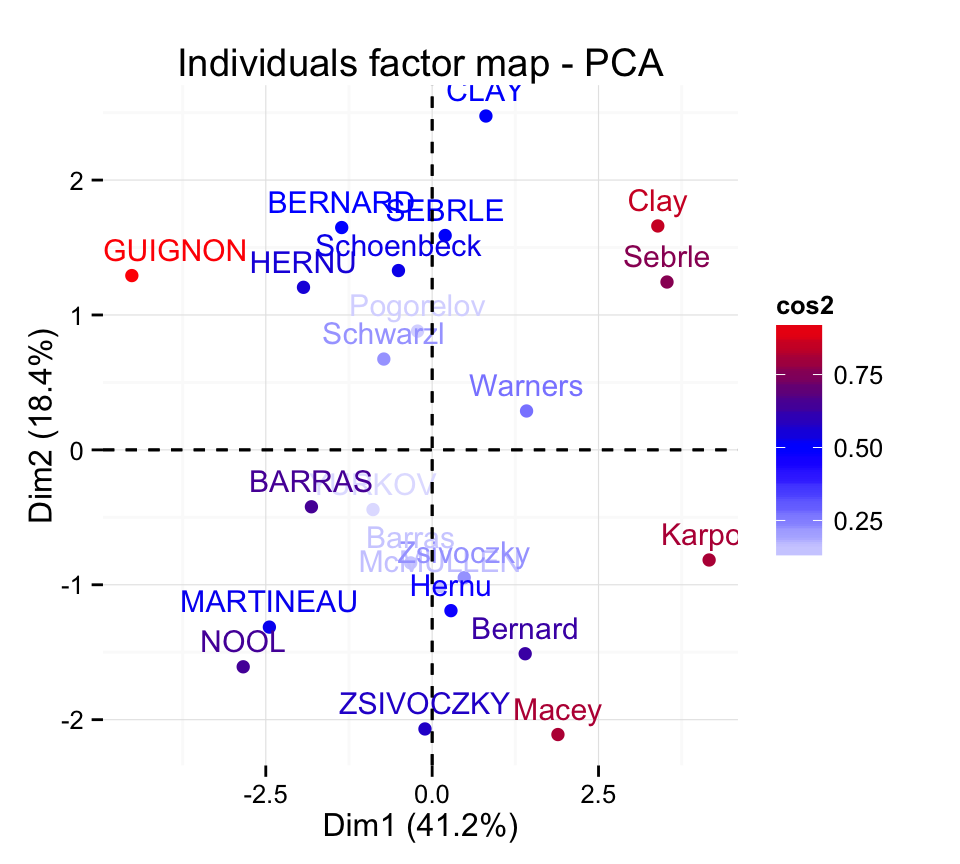

FactoMineR and factoextra : Principal component analysis - R software and data mining

Read more about ggplot2 themes here : ggplot2 themes and background colors

Make a biplot of individuals and variables :

fviz_pca_biplot(res.pca,  geom = "text")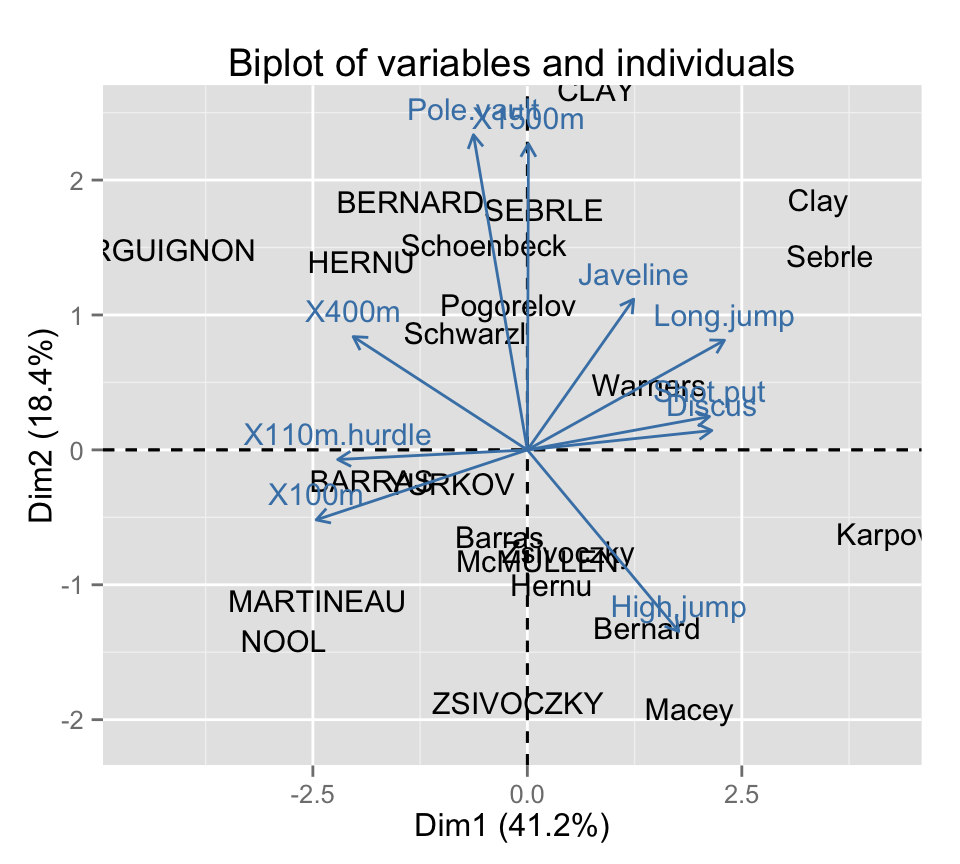

FactoMineR and factoextra : Principal component analysis - R software and data mining

Change the color of individuals by groups

We will use iris data sets in this section :

data(iris)
head(iris)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa
# The variable Species (index = 5) is removed
# before PCA analysis
iris.pca <- PCA(iris[,-5], graph = FALSE)

Individuals factor map :

# Default plot
fviz_pca_ind(iris.pca, label="none")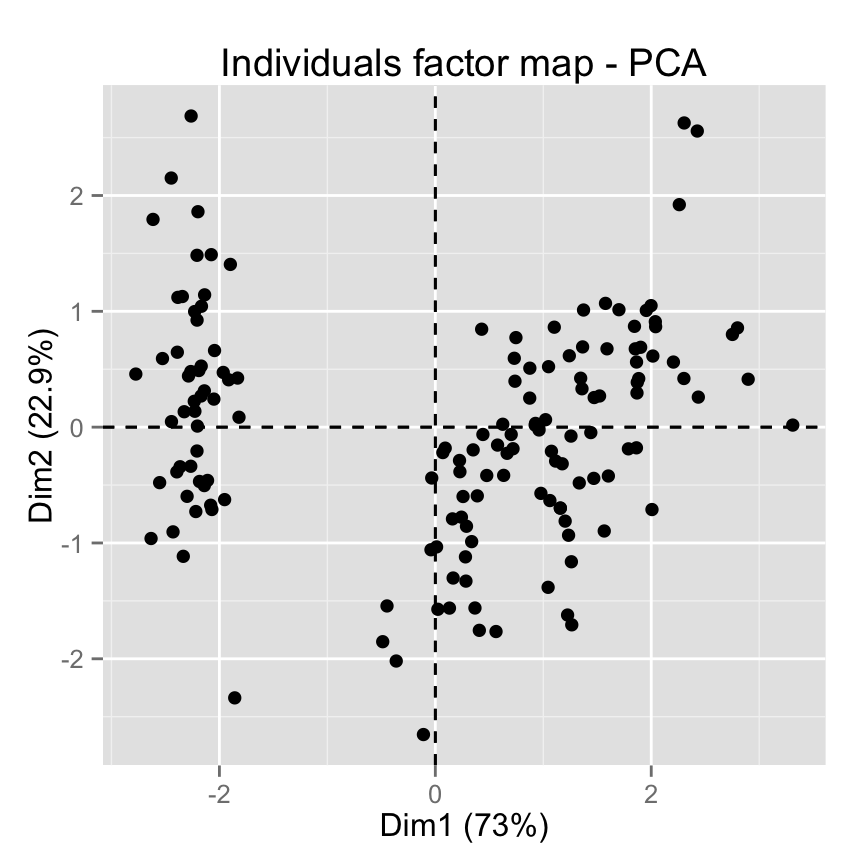

FactoMineR and factoextra : Principal component analysis - R software and data mining

Change individual colors by groups :

fviz_pca_ind(iris.pca,  label="none", habillage=iris$Species)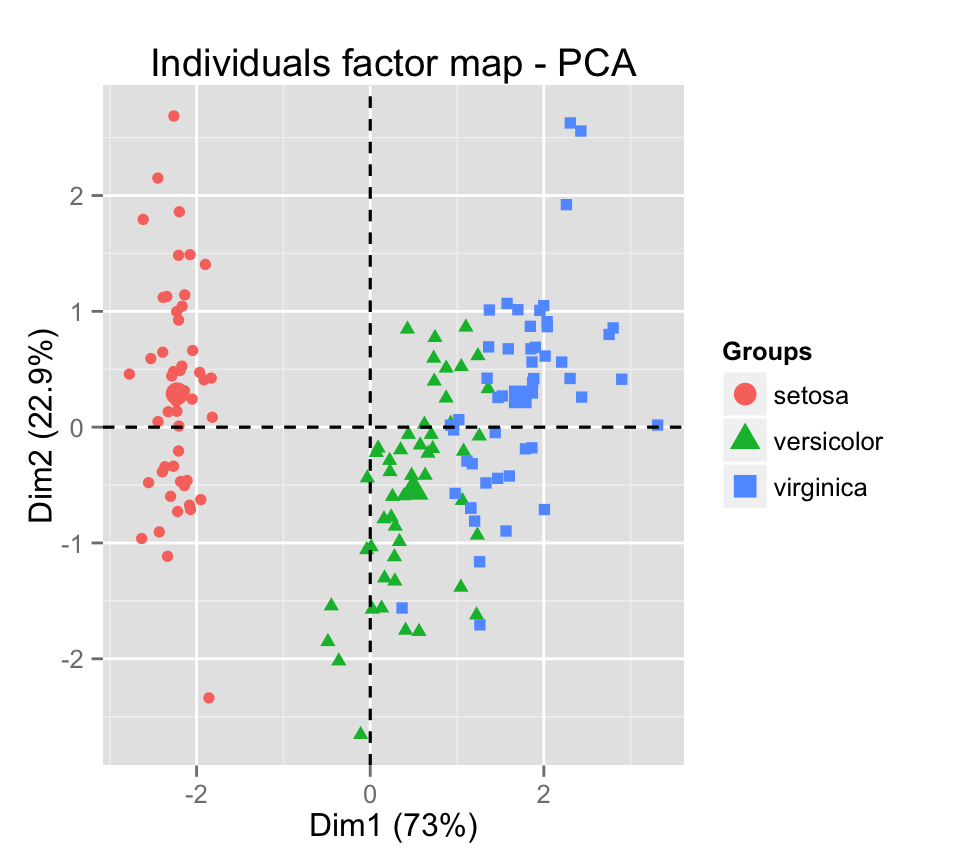

FactoMineR and factoextra : Principal component analysis - R software and data mining

Add ellipses of point concentrations : the argument habillage is used to specify the factor variable for coloring the observations by groups.

fviz_pca_ind(iris.pca, label="none", habillage=iris$Species,
             addEllipses=TRUE, ellipse.level=0.95)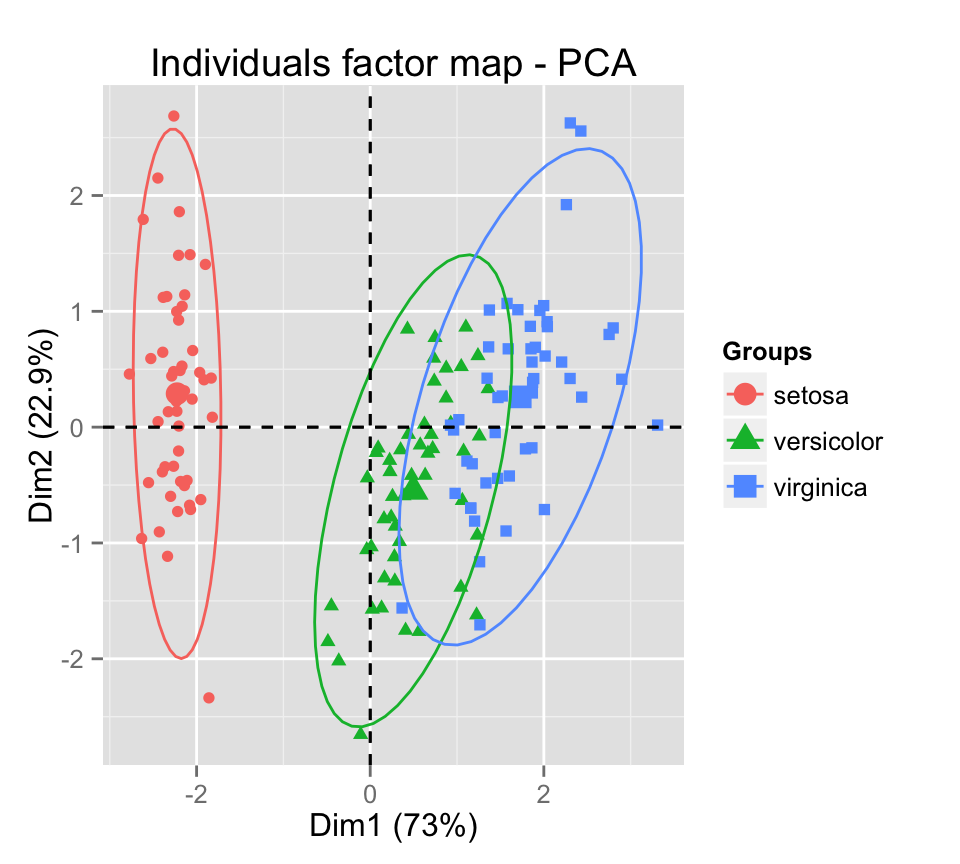

FactoMineR and factoextra : Principal component analysis - R software and data mining

Now, let’s :

  • make a biplot of individuals and variables
  • change the color of individuals by groups
  • change the transparency of variable colors by their contribution values
  • show only the labels for variables
fviz_pca_biplot(iris.pca, 
  habillage = iris$Species, addEllipses = TRUE,
  col.var = "red", alpha.var ="cos2",
  label = "var") +
  scale_color_brewer(palette="Dark2")+
  theme_minimal()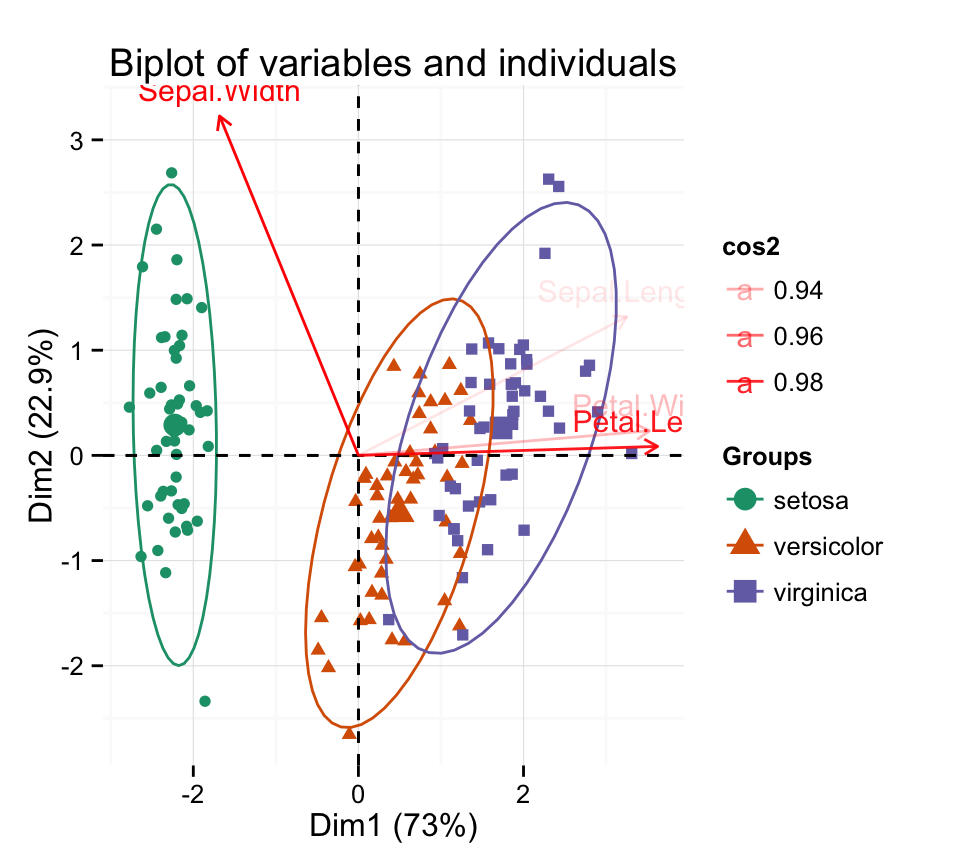

FactoMineR and factoextra : Principal component analysis - R software and data mining

Principal component analysis using supplementary individuals and variables

As described above, the data sets decathlon2 contain supplementary continuous variables (quanti.sup, columns 11:12), supplementary qualitative variables (quali.sup, column 13) and supplementary individuals (ind.sup, rows 24:27)

Supplementary variables and individuals are not used for the determination of the principal components. Their coordinates are predicted using only the informations provided by the performed principal component analysis on active variables/individuals.

To specify supplementary individuals and variables, the function PCA() can be used as follow :

PCA(X, scale.unit = TRUE, ncp = 5, ind.sup = NULL,
    quanti.sup=NULL, quali.sup=NULL, graph=TRUE, axes = c(1,2))

  • X : a data frame. Rows are individuals and columns are numeric variables.
  • scale.unit : a logical value. If TRUE, the data are scaled to unit variance before the analysis.
  • ncp : number of dimensions kept in the final results.
  • ind.sup : a numeric vector specifying the indexes of the supplementary individuals
  • quanti.sup, quali.sup : a numeric vector specifying, respectively, the indexes of the quantitative and qualitative variables
  • graph : a logical value. If TRUE a graph is displayed.
  • axes : a vector of length 2 specifying the components to be plotted


Example of usage :

res.pca <- PCA(decathlon2, ind.sup=24:27, 
               quanti.sup = 11:12, quali.sup = 13, graph=FALSE)

Visualize supplementary quantitative variables

All the results (coordinates, correlation and cos2) for the supplementary quantitative variables can be extracted as follow :

res.pca$quanti.sup
$coord
            Dim.1       Dim.2      Dim.3       Dim.4       Dim.5
Rank   -0.7014777 -0.24519443 -0.1834294  0.05575186 -0.07382647
Points  0.9637075  0.07768262  0.1580225 -0.16623092 -0.03114711
$cor
            Dim.1       Dim.2      Dim.3       Dim.4       Dim.5
Rank   -0.7014777 -0.24519443 -0.1834294  0.05575186 -0.07382647
Points  0.9637075  0.07768262  0.1580225 -0.16623092 -0.03114711
$cos2
           Dim.1       Dim.2      Dim.3      Dim.4        Dim.5
Rank   0.4920710 0.060120310 0.03364635 0.00310827 0.0054503477
Points 0.9287322 0.006034589 0.02497110 0.02763272 0.0009701427

Variables factor map using FactoMineR base graph :

plot(res.pca, choix = "var")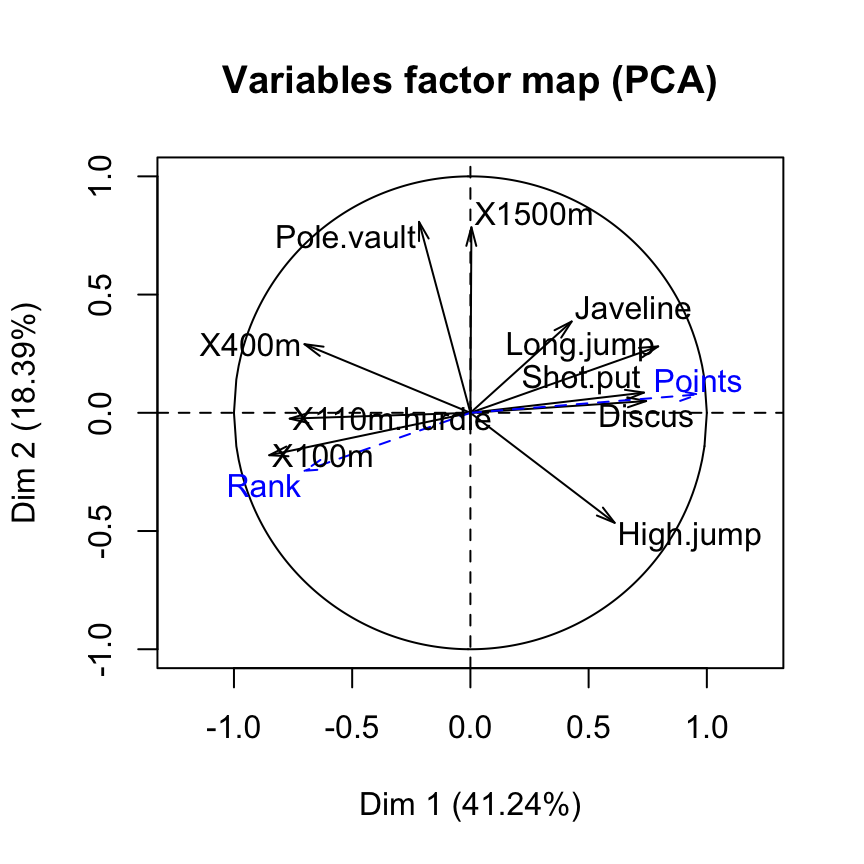

FactoMineR and factoextra : Principal component analysis - R software and data mining

Supplementary quantitative variables are shown in blue color and dashed lines.

It’s also possible to make the variables factor map using factoextra :

fviz_pca_var(res.pca)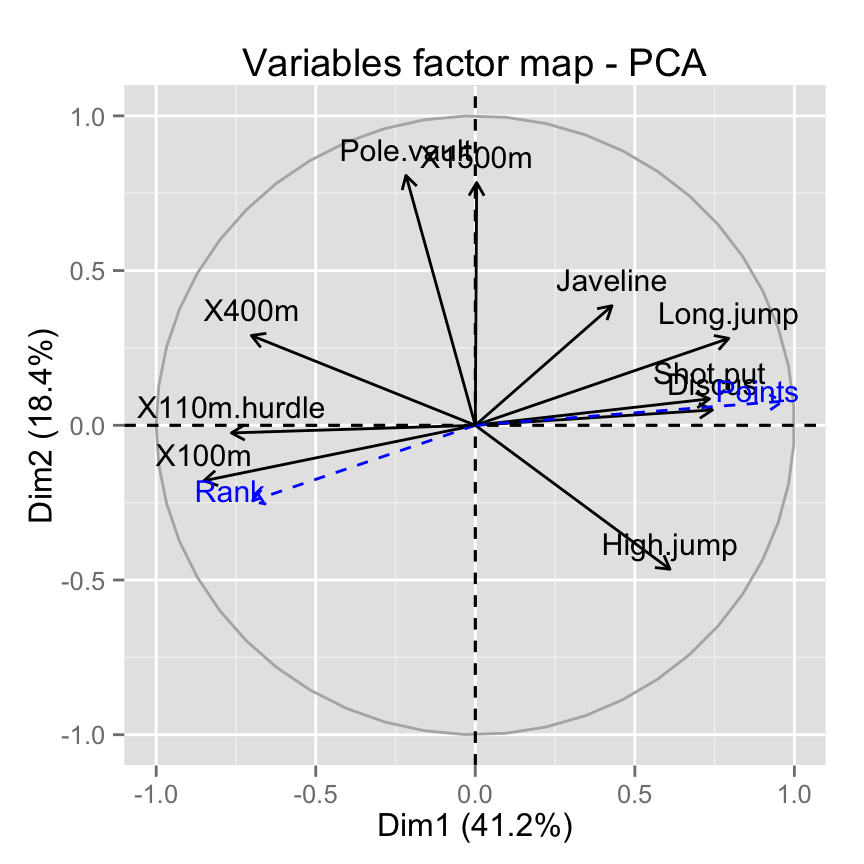

FactoMineR and factoextra : Principal component analysis - R software and data mining

Visualize supplementary individuals

The data sets decathlon2 contain some supplementary individuals from row 24 to 27.

# Data for the supplementary individuals
ind.sup <- decathlon2[24:27, 1:10]
ind.sup[, 1:6]
         X100m Long.jump Shot.put High.jump X400m X110m.hurdle
KARPOV   11.02      7.30    14.77      2.04 48.37        14.09
WARNERS  11.11      7.60    14.31      1.98 48.68        14.23
Nool     10.80      7.53    14.26      1.88 48.81        14.80
Drews    10.87      7.38    13.07      1.88 48.51        14.01

Individuals factor map using FactoMineR base graph :

plot(res.pca, choix="ind")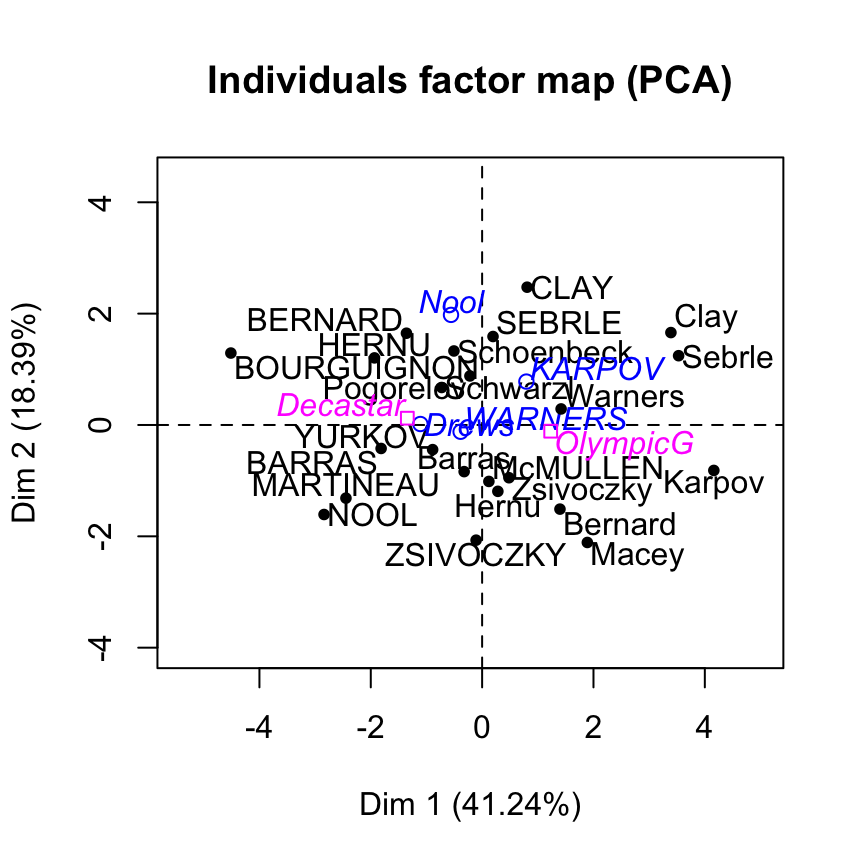

FactoMineR and factoextra : Principal component analysis - R software and data mining

Supplementary individuals are shown in blue. The levels of the supplementary qualitative variable are shown in magnenta color.

The results for supplementary individuals can be extracted as follow :

res.pca$ind.sup
$coord
              Dim.1       Dim.2      Dim.3      Dim.4       Dim.5
KARPOV    0.7947206  0.77951227 -1.6330203  1.7242283 -0.75070396
WARNERS  -0.3864645 -0.12159237 -1.7387332 -0.7063341 -0.03230011
Nool     -0.5591306  1.97748871 -0.4830358 -2.2784526 -0.25461493
Drews    -1.1092038  0.01741477 -3.0488182 -1.5343468 -0.32642192
$cos2
              Dim.1        Dim.2      Dim.3      Dim.4        Dim.5
KARPOV   0.05104677 4.911173e-02 0.21553730 0.24028620 0.0455487744
WARNERS  0.02422707 2.398250e-03 0.49039677 0.08092862 0.0001692349
Nool     0.02897149 3.623868e-01 0.02162236 0.48108780 0.0060077529
Drews    0.09207094 2.269527e-05 0.69560547 0.17617609 0.0079736753
$dist
 KARPOV  WARNERS     Nool    Drews  
3.517470 2.482899 3.284943 3.655527

Supplementary qualitative variables

The data sets decathlon2 contain a supplementary qualitative variable at columns 13 corresponding to the type of competitions.

Qualitative variable can be helpful for interpreting the data and for coloring individuals by groups.

The argument habillage is used to specify the index of the supplementary qualitative variable :

plot(res.pca, choix = "ind", habillage = 13)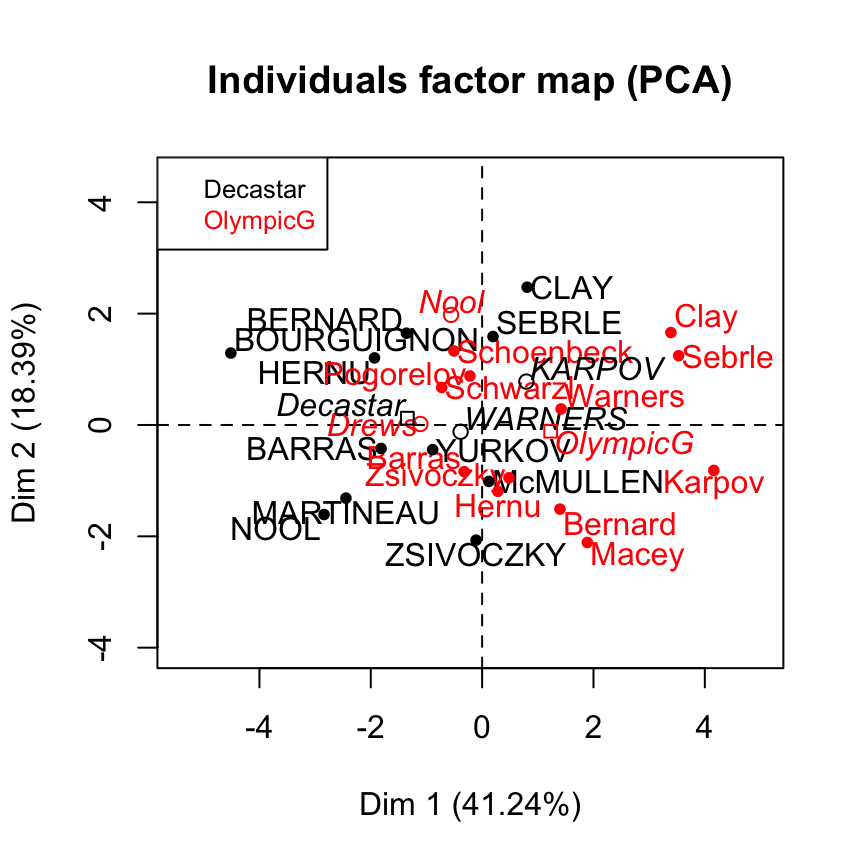

FactoMineR and factoextra : Principal component analysis - R software and data mining

It’s also possible to use factoextra :

fviz_pca_ind(res.pca, habillage = 13,
  addEllipses =TRUE, ellipse.level = 0.68) +
  scale_color_brewer(palette="Dark2") +
  theme_minimal()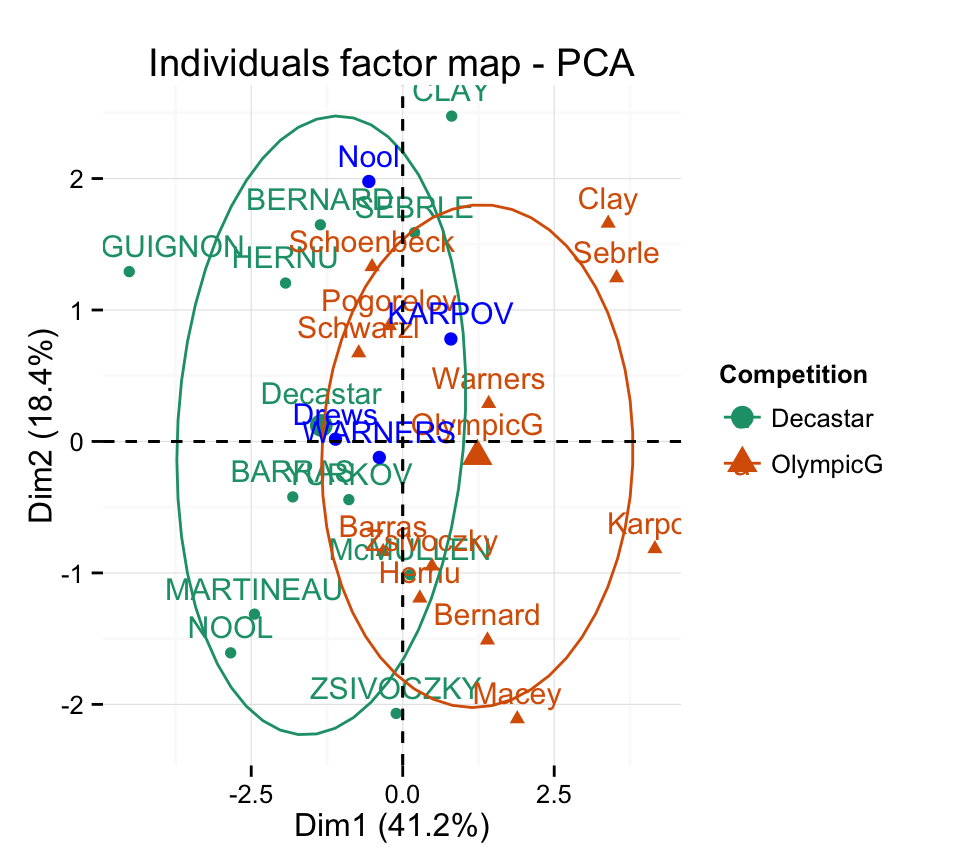

FactoMineR and factoextra : Principal component analysis - R software and data mining

Supplementary individuals are shown in blue color

The results concerning the supplementary qualitative variable are :

res.pca$quali
$coord
             Dim.1      Dim.2       Dim.3      Dim.4      Dim.5
Decastar -1.343451  0.1218097 -0.03789524  0.1808357  0.1343364
OlympicG  1.231497 -0.1116589  0.03473730 -0.1657661 -0.1231417
$cos2
             Dim.1       Dim.2        Dim.3      Dim.4       Dim.5
Decastar 0.9051233 0.007440939 0.0007201669 0.01639956 0.009050062
OlympicG 0.9051233 0.007440939 0.0007201669 0.01639956 0.009050062
$v.test
             Dim.1      Dim.2      Dim.3      Dim.4      Dim.5
Decastar -2.970766  0.4034256 -0.1528767  0.8971036  0.7202457
OlympicG  2.970766 -0.4034256  0.1528767 -0.8971036 -0.7202457
$dist
Decastar OlympicG 
1.412108 1.294433 
$eta2
                Dim 1      Dim 2       Dim 3      Dim 4      Dim 5
Competition 0.4011568 0.00739783 0.001062332 0.03658159 0.02357972

Dimension description

The function dimdesc() can be used to identify the most correlated variables with a given principal component.

A simplified format is :

dimdesc(res, axes = 1:3, proba = 0.05)

  • res : an object of class PCA
  • axes : a numeric vector specifying the dimensions to be described
  • prob : the significance level


Example of usage :

res.desc <- dimdesc(res.pca, axes = c(1,2))
# Description of dimension 1
res.desc$Dim.1
$quanti
             correlation      p.value
Points         0.9637075 1.605675e-13
Long.jump      0.7941806 6.059893e-06
Discus         0.7432090 4.842563e-05
Shot.put       0.7339127 6.723102e-05
High.jump      0.6100840 1.993677e-03
Javeline       0.4282266 4.149192e-02
Rank          -0.7014777 1.917657e-04
X400m         -0.7016034 1.910387e-04
X110m.hurdle  -0.7641252 2.195812e-05
X100m         -0.8506257 2.727129e-07
$quali
                   R2     p.value
Competition 0.4011568 0.001177378
$category
          Estimate     p.value
OlympicG  1.287474 0.001177378
Decastar -1.287474 0.001177378
# Description of dimension 2
res.desc$Dim.2
$quanti
           correlation      p.value
Pole.vault   0.8074511 3.205016e-06
X1500m       0.7844802 9.384747e-06
High.jump   -0.4652142 2.529390e-02

Infos

This analysis has been performed using R software (ver. 3.1.2) and ggplot2 (ver. )


Enjoyed this article? I’d be very grateful if you’d help it spread by emailing it to a friend, or sharing it on Twitter, Facebook or Linked In.

Show me some love with the like buttons below... Thank you and please don't forget to share and comment below!!
Avez vous aimé cet article? Je vous serais très reconnaissant si vous aidiez à sa diffusion en l'envoyant par courriel à un ami ou en le partageant sur Twitter, Facebook ou Linked In.

Montrez-moi un peu d'amour avec les like ci-dessous ... Merci et n'oubliez pas, s'il vous plaît, de partager et de commenter ci-dessous!