The different types of correlation methods

There are :

• the Pearson correlation method which is a parametric correlation test as it depends on the distribution of the data. This method measures the linear dependence between two variables.
• the Kendall and Spearman rank-based correlation analysis (non-parametric methods). These two methods are recommended if the data do not come from a bivariate normal distribution.

Pearson correlation test is the most commonly used method to calculate the correlation coefficient between two variables. The formula is shown in the next section.

(Designed by Freepik)

Pearson correlation coefficient formula

The Pearson correlation coefficient between two variables, x and y, can be calculated using the formula below :

\[ r = \frac{\sum{(x-m_x)(y-m_y)}}{\sqrt{\sum{(x-mx)^2}\sum{(y-my)^2}}} \]

\(m_x\) and \(m_y\) are the means of x and y variables.

The significance level of the correlation can be determined by reading the table of critical values for the degrees of freedom : \(df = n-2\)

Read more : correlation formula

Calculate the correlation coefficient using R software

Correlation coefficient can be easily computed in R using the function cor() or cor.test(). The simplified formats are :

cor(x, y, method = c("pearson", "kendall", "spearman"))
cor.test(x, y, method=c("pearson", "kendall", "spearman"))

In the R code above x and y are two numeric vectors with the same length.

These functions can be used as follow :

# Define two numeric vectors
x <- c(44.4, 45.9, 41.9, 53.3, 44.7, 44.1, 50.7, 45.2, 60.1)
y <- c( 2.6,  3.1,  2.5,  5.0,  3.6,  4.0,  5.2,  2.8,  3.8)
# Pearson correlation coefficient between x and y
cor(x, y)

[1] 0.5712

# Pearson correlation test 
cor.test(x, y)

    Pearson's product-moment correlation
data:  x and y
t = 1.841, df = 7, p-value = 0.1082
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1497  0.8956
sample estimates:
   cor 
0.5712 

The correlation coefficient is 0.5712 and the p-value is 0.1082.

Read more : correlation analysis using R software

Spearman and Kendall non-parametric correlation methods can be used as follow :

# Spearman non-parametric correlation test
cor.test(x, y, method="spearman")
# Kendall non-parametric correlation test
cor.test(x, y, method="kendall")

Interpretation of the correlation coefficient

The value of the correlation coefficient is comprised between -1 and 1

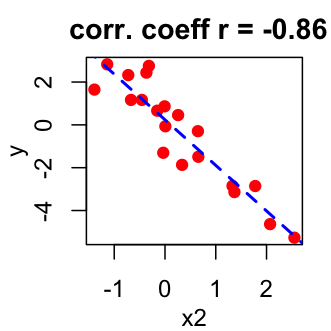
• -1 corresponds to a strong negative correlation : this means that every time x increases, y decreases (left panel figure)
• 0 means that there is no association between the two variables (x and y) (middle panel figure)
• 1 corresponds to a strong positive correlation : this means that y increases with x (right panel figure)

Online correlation coefficient calculator

A web application, for computing the different correlation coefficients, is available at this link : correlation coefficient calculator.

It can be used online without any installation to calculate Pearson, Kendall or Spearman correlation coefficient.

(Designed by Freepik)

Go to the correlation coefficient calculator

The correlation coefficient calculator can be used as follow :

1. Go to the application available at this link : correlation coefficient calculator
2. Copy and paste your data from Excel to the calculator. You can use the demo data available in the calculator web page by clicking on the link.
3. Select the correlation methods (Pearson, Spearman or Kendall). Default is the Pearson method.
4. Click the OK button

Recommended for you