Define correlation

Correlation is very helpful to investigate the dependence between two or more variables. As an example we are interested to know whether there is an association between the weights of fathers and son. correlation coefficient can be calculated to answer this question.

If there is no relationship between the two variables (father and son weights), the average weight of son should be the same regardless of the weight of the fathers and vice versa.

There are different methods to perform correlation analysis : Pearson, Kendall and Spearman correlation tests.

The most commonly used is Pearson correlation. The aim of this article is to describe Pearson correlation formula.

Pearson correlation

Pearson correlation measures a linear dependence between two variables (x and y). It’s also known as a parametric correlation test because it depends to the distribution of the data. The plot of y = f(x) is named linear regression curve.

The pearson correlation formula is :

\[ r = \frac{\sum{(x-m_x)(y-m_y)}}{\sqrt{\sum{(x-mx)^2}\sum{(y-my)^2}}} \]

\(m_x\) and \(m_y\) are the means of x and y variables.

the p-value (significance level) of the correlation can be determined :

1. by using the correlation coefficient table for the degrees of freedom : \(df = n-2\)

2. or by calculating the t value : \[ t=\frac{r}{\sqrt{1-r^2}}\sqrt{n-2} \]

In this case the corresponding p-value is determined using t distribution table for \(df = n-2\)

If the p-value is less than 5%, then the correlation is significant.

Interpretation of correlation coefficient

Correlation coefficient is between -1 (strong negative correlation) and 1 (strong positive correlation)

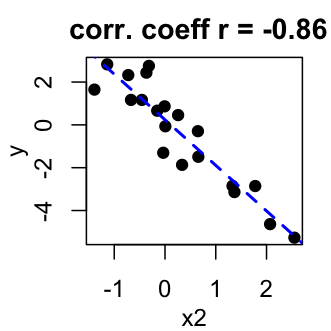
Correlation coefficient calculator

Recommended for you