Correlation matrix : A quick start guide to analyze, format and visualize a correlation matrix using R software

This article has been updated, you are now consulting an old release of this article!

What is correlation matrix

Correlation matrix or covariance matrix is used to investigate the dependence between multiple variables at the same time. The result is a table containing the coefficients of correlation between each variable and the others. There are different methods for correlation analysis : Pearson correlation test, Spearman and Kendall rank-based correlation analysis. These methods are discussed in the next sections. Correlation matrix can be visualized using correlogram. The aim of this article is to show you how to compute and visualize a correlation matrix in R.

Note that online software is also available here to compute correlation matrix and to plot a correlogram without any installation.

Correlation analysis in R

The R function cor() can be used to compute a correlation matrix. A simplified format of the function is :

# x is a matrix or data.frame
cor(x, method = c("pearson", "kendall", "spearman"))

The argument method= indicates the correlation coefficient to be computed. The default is pearson correlation coefficient which measures the linear dependence between two variables. kendall and spearman correlation methods are non-parametric rank-based correlation test.

data for correlation analysis

The mtcars data is used in the following examples to compute the correlation matrix.

head(mtcars)
                   mpg cyl disp  hp drat    wt  qsec vs am gear carb
Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

Correlation matrix

mcor <- cor(mtcars)
mcor
       mpg   cyl  disp    hp  drat    wt  qsec    vs    am  gear  carb
mpg   1.00 -0.85 -0.85 -0.78  0.68 -0.87  0.42  0.66  0.60  0.48 -0.55
cyl  -0.85  1.00  0.90  0.83 -0.70  0.78 -0.59 -0.81 -0.52 -0.49  0.53
disp -0.85  0.90  1.00  0.79 -0.71  0.89 -0.43 -0.71 -0.59 -0.56  0.39
hp   -0.78  0.83  0.79  1.00 -0.45  0.66 -0.71 -0.72 -0.24 -0.13  0.75
drat  0.68 -0.70 -0.71 -0.45  1.00 -0.71  0.09  0.44  0.71  0.70 -0.09
wt   -0.87  0.78  0.89  0.66 -0.71  1.00 -0.17 -0.55 -0.69 -0.58  0.43
qsec  0.42 -0.59 -0.43 -0.71  0.09 -0.17  1.00  0.74 -0.23 -0.21 -0.66
vs    0.66 -0.81 -0.71 -0.72  0.44 -0.55  0.74  1.00  0.17  0.21 -0.57
am    0.60 -0.52 -0.59 -0.24  0.71 -0.69 -0.23  0.17  1.00  0.79  0.06
gear  0.48 -0.49 -0.56 -0.13  0.70 -0.58 -0.21  0.21  0.79  1.00  0.27
carb -0.55  0.53  0.39  0.75 -0.09  0.43 -0.66 -0.57  0.06  0.27  1.00

In the table above correlations coefficients between the possible pairs of variables are shown.

If your data contain missing values, use the following R code to handle missing values by case-wise deletion.

cor(mtcars, use = "complete.obs")

Correlation significance levels (p-value)

The output of cor() function is the correlation coefficients between each variable and the others. However the function doesn’t display the correlation signicance levels (p-value). In the next section, we will use Hmisc R package to calculate correlation p-value.

The function rcorr() from Hmisc package can be used to compute the significance levels for pearson and spearman correlations. Using this function, Pearson’s r or Spearman’s rho rank correlation coefficients are computed for all possible pairs of columns in the data table.

The simplified format is :

rcorr(x, type=c("pearson","spearman"))

x should be a matrix. The correlation type can be pearson or spearman.

library(Hmisc)
rcorr(as.matrix(mtcars[,1:7]))
       mpg   cyl  disp    hp  drat    wt  qsec
mpg   1.00 -0.85 -0.85 -0.78  0.68 -0.87  0.42
cyl  -0.85  1.00  0.90  0.83 -0.70  0.78 -0.59
disp -0.85  0.90  1.00  0.79 -0.71  0.89 -0.43
hp   -0.78  0.83  0.79  1.00 -0.45  0.66 -0.71
drat  0.68 -0.70 -0.71 -0.45  1.00 -0.71  0.09
wt   -0.87  0.78  0.89  0.66 -0.71  1.00 -0.17
qsec  0.42 -0.59 -0.43 -0.71  0.09 -0.17  1.00
n= 32 
P
     mpg    cyl    disp   hp     drat   wt     qsec  
mpg         0.0000 0.0000 0.0000 0.0000 0.0000 0.0171
cyl  0.0000        0.0000 0.0000 0.0000 0.0000 0.0004
disp 0.0000 0.0000        0.0000 0.0000 0.0000 0.0131
hp   0.0000 0.0000 0.0000        0.0100 0.0000 0.0000
drat 0.0000 0.0000 0.0000 0.0100        0.0000 0.6196
wt   0.0000 0.0000 0.0000 0.0000 0.0000        0.3389
qsec 0.0171 0.0004 0.0131 0.0000 0.6196 0.3389

As an output, the rcorr() function returns a list with elements : - r : the matrix of correlations - n : the matrix of number of observations used in analyzing each pair of variables - P : the p-values corresponding to the significance levels of correlations.

Correlogram : Visualization of correlation matrix

Several methods are available to plot a correlogram in R. You can use either R symnum function, corrplot function or scatter graph to make a graph of correlation matrix.

Use symnum function

The R function symnum replaces correlation coefficients by symbols according to the value. It takes the correlation matrix as an argument :

symnum(mcor)
     m cy ds h dr w q v a g cr
mpg  1                        
cyl  + 1                      
disp + +  1                   
hp   , +  ,  1                
drat , ,  ,  . 1              
wt   + ,  +  , ,  1           
qsec . .  .  ,      1         
vs   , +  ,  , .  . , 1       
am   . .  .    ,  ,     1     
gear . .  .    ,  .     , 1   
carb . .  .  ,    . , .     1 
attr(,"legend")
[1] 0 ' ' 0.3 '.' 0.6 ',' 0.8 '+' 0.9 '*' 0.95 'B' 1

As indicated in the legend, the correlation coefficients between 0 and 0.3 are replaced by a space (" “); correlation coefficients between 0.3 and 0.6 are replace by”.“; etc …

Correlogram using R corrplot function

You have to install corrplot package which performs a graphical display of a correlation matrix in R.

To read more about corplot() function click here : visualize a correlation matrix using corrplot.

The function corrplot takes the correlation matrix as the first argument. The second argument (type=“upper”) is used to display only the upper triangular of the correlation matrix.

library(corrplot)
corrplot(mcor, type="upper", order="hclust", tl.col="black", tl.srt=45)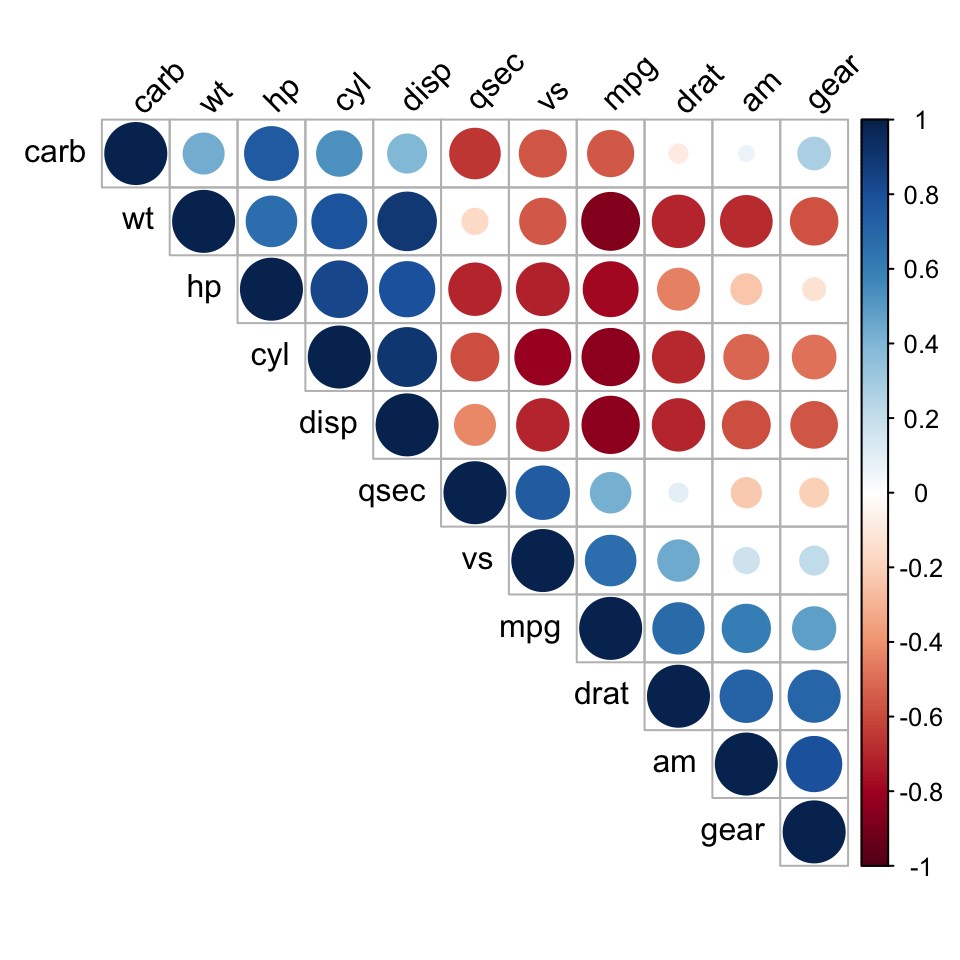

plot of chunk correlogram

Positive correlations are displayed in blue and negative correlations in red color. Color intensity and the size of the circle are proportional to the correlation coefficients. In the right side of the correlogram, the legend color shows the correlation coefficients and the corresponding colors.

The correlation matrix is reordered according to the correlation coefficient using “hclust” method. tl.col (for text label color) and tl.srt (for text label string rotation) are used to change text colors and rotations.

conclusinons

  • Use cor() function for simple correlation analysis
  • Use rcorr() function from Hmisc package to compute matrix of correlation coefficient and matrix of p-value in single step.
  • Use symnum() function or corplot() function [from corrplot package] to make a graph of a correlation matrix

Infos

This analysis was performed using R (ver. 3.1.0).

Enjoyed this article? I’d be very grateful if you’d help it spread by emailing it to a friend, or sharing it on Twitter, Facebook or Linked In.

Show me some love with the like buttons below... Thank you and please don't forget to share and comment below!!
Avez vous aimé cet article? Je vous serais très reconnaissant si vous aidiez à sa diffusion en l'envoyant par courriel à un ami ou en le partageant sur Twitter, Facebook ou Linked In.

Montrez-moi un peu d'amour avec les like ci-dessous ... Merci et n'oubliez pas, s'il vous plaît, de partager et de commenter ci-dessous!