Exploratory data analysis

Introduction

The aim of EDA (exploratory data analysis) is to familiarize ourselves with data when we analyze genomic data. Some basic EDA tools include histogram, the Q-Q plot, scatter plot, box plot, stratification, log transformation and other summary statistics.

Histograms

Firstly, load the R library UsingR which contains several examples including one data set called father.son that has heights for fathers and sons.

library(UsingR)
x=father.son$fheight

Histogram is a visual description of the distribution of data.

hist(x,breaks=seq(floor(min(x)),ceiling(max(x))),main="", xlab="Height")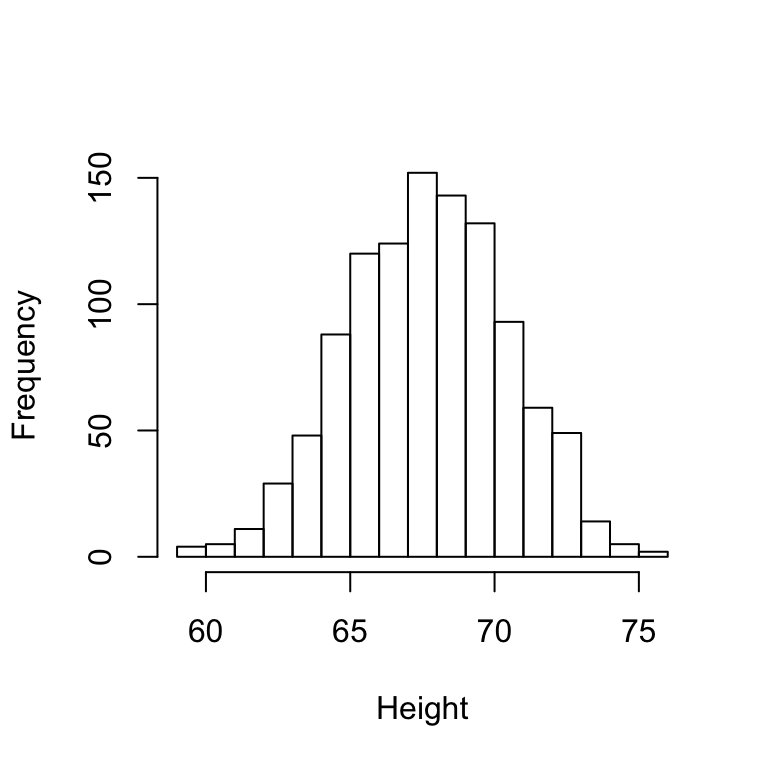

Notice that breaks are the the intervals, in which to make count of individuals. We decide to look at the following breaks: 59 to 60, 60 to 61, etc. Note that with this simple plot we can approximate the number of individuals in any given interval. Y axis (Frequency) is the number of individuals in a given interval. For example, there are about 70 individuals over six feet (72 inches) tall.

Another plot that’s related to the histogram is the empirical commutative distribution function (ecdf). It reports for any given number the percent of individuals that are below that threshold.

#The number for which, we want to compute proportions
xs<-seq(floor(min(x)),ceiling(max(x)),0.1)
plot(xs,ecdf(x)(xs),type="l",xlab="x=Height",ylab="F(x)")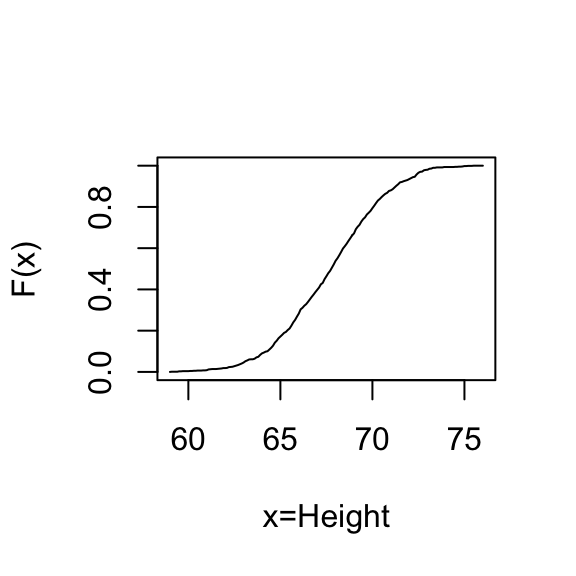

xs is the numbers for which, we want to compute these proportions for. The function ecdf of x creates a function that then you can feed these values in, and it’ll give you back these proportions. We can make a plot of that.

For any value, say, 70, you can see that about 70% to 75% of our individuals are shorter than 70 inches.

Normal approximation

The probability distribution we see above approximates one that is very common in a nature: the bell curve or normal distribution or Gaussian distribution. When the histogram of a list of numbers approximates the normal distribution we can use a convenient mathematical formula to approximate the proportion of individuals in any given interval

\[ \mbox{Pr}(a < x < b) = \int_a^b \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( \frac{-(x-\mu)^2}{2 \sigma^2} \right)} \, dx \]

Here \(\mu\) and \(\sigma\) are refereed to as the mean and standard deviation. So, in the case of normal distribution, we just have to know the mean \(\mu\) and the standard deviation \(\sigma\) of the data to describe the entire distribution.

For example, the proportion of individuals that are taller than 70 can be computed using the following code :

1-pnorm(70, mean(x), sd(x)) #right part of distibution

## [1] 0.1997

The proportion of individuals with height less than 70 is given by :

pnorm(70, mean(x), sd(x)) #left part of the distribution

## [1] 0.8003

To check whether a data follows the normal approximation, we can use Q-Q plots (quantile-quantile plot).

QQ-plot

As mentioned above, quantile-quantile plots is used to check whether a data follows normal distribution.

The procedures are to :

1. Calculate sample percentiles (1%, 2%, ….., 50%, 99%). So we compute, what is the number for which 1% of the data is below that number? 2%, 3%, 4%, and we compute what are called the percentiles.
2. Calculate the theoretical percentiles predicted by the normal distribution
3. Make a plot to see whether they fit

#percentile
ps <- seq(0.01,0.99,0.01)
qs <- quantile(x,ps)
#theorical percentiles
normalqs <- qnorm(ps,mean(x),sd(x))
#Plot
plot(normalqs,qs,xlab="Normal percentiles",ylab="Height percentiles")
abline(0,1) ##identity line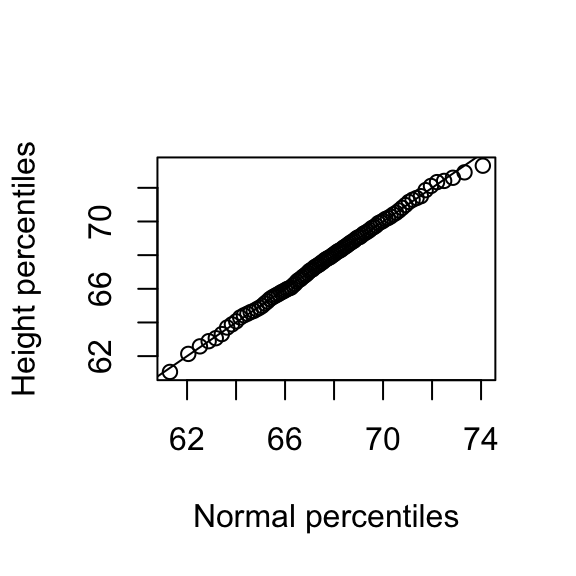

Note how close these values are. 

Also note that we can do same with less code

qqnorm(x)
qqline(x)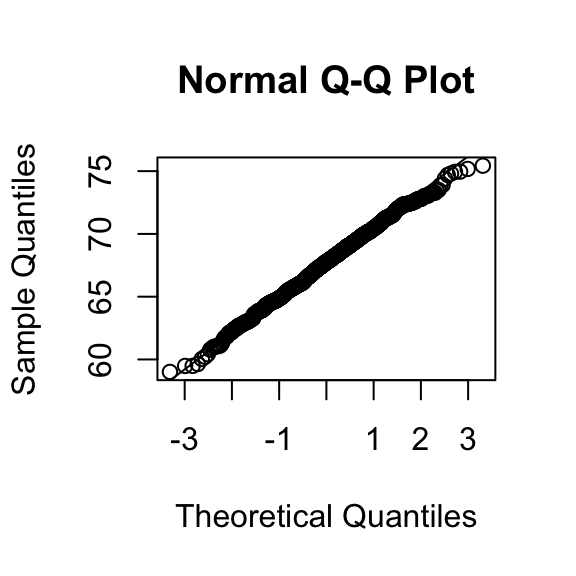

Box-plot

Data is not always normally distributed. An example of data that is not normally distributed are salaries. In these cases the mean and the standard deviation are not good summaries.

#salaries
hist(exec.pay)
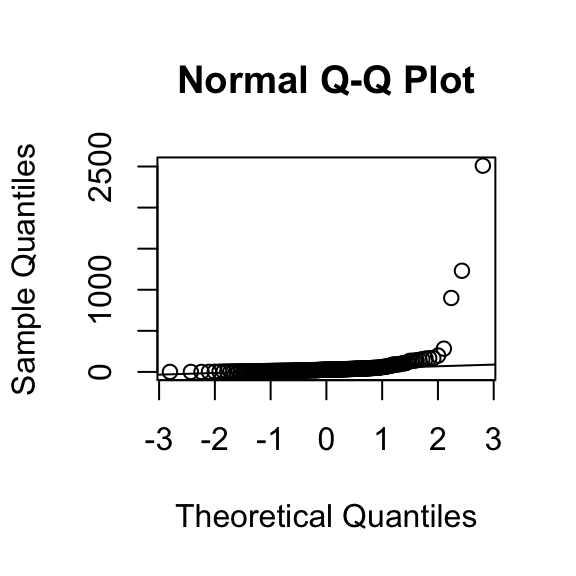
qqnorm(exec.pay)
qqline(exec.pay)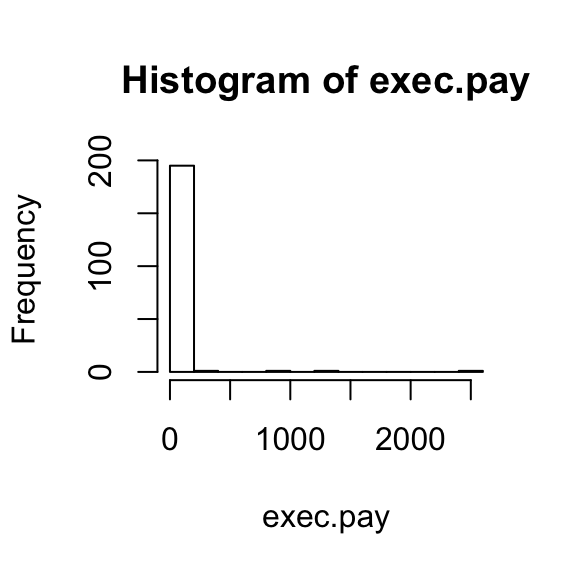

If data is not normal distributed, box plot is better to summarize the data. A practical summary is to compute 3 percentiles: 25-th, 50-th (the median) and the 75-th. A box plots shows these 3 values along with a range calculated as median \(\pm\) 1.5 75-th percentiles - 25th-percentile. Values outside this range are shown as points.

boxplot(exec.pay,ylab="10,000s of dollars",ylim=c(0,400))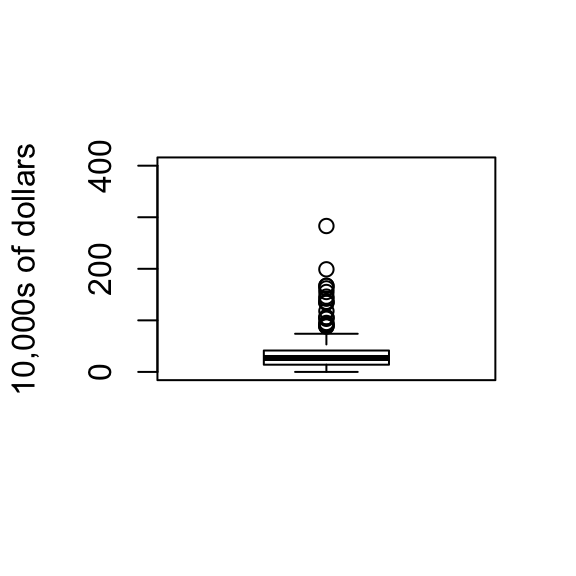

Scatter plots and correlation

Scatter plots are used to study the relationship between two or more variables. A classic examples is the father/son height data.

data("father.son")
x=father.son$fheight
y=father.son$sheight
plot(x,y,xlab="Father's height in inches",
     ylab="Son's height in inches",
     main=paste("correlation =",signif(cor(x,y),2)))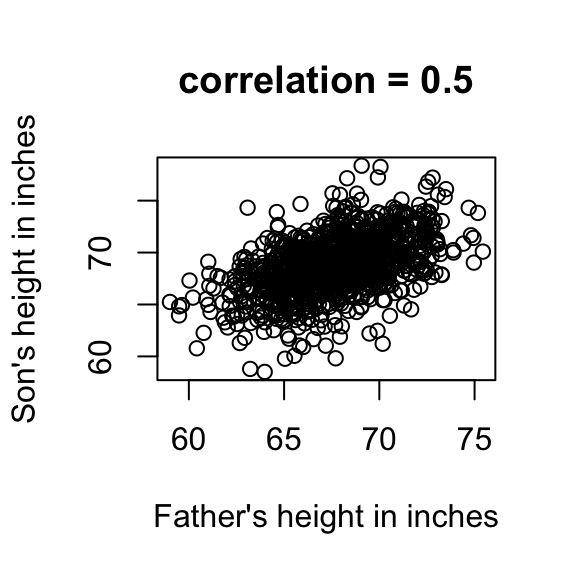

The scatter plot shows a general trend : the taller the father the taller to son. A summary of this trend is the correlation coefficient which in this cases is 0.5. Correlation helps to make prediction by computing regression line.

When two variables follow a bivariate normal distribution then for any given value of x we predict the value of y with :

\[ \frac{Y - \mu_Y}{\sigma_Y} = r \frac{X-\mu_X}{\sigma_X} \]

with the \(\mu\) representing the averages, \(\sigma\) the standard deviations, and \(r\) the correlation.

If you turn the two data in standard units, the correlation coefficient is the slope of the line that we used to predict variable y given variable x.

We have to be careful with **non-normal data**. We can use Spearman's correlation to obtain a robust estimate of the correlation in this case.

Spearman’s correlation

In the case of non-normal data, the average and standard deviation are not good summaries. Examples include cases in which one variable is related to another by a parabolic function. Another, more common example are caused by outliers or extreme values.

a=rnorm(100);a[1]=10
b=rnorm(100);b[1]=11
plot(a,b,main=paste("correlation =",signif(cor(a,b),2)))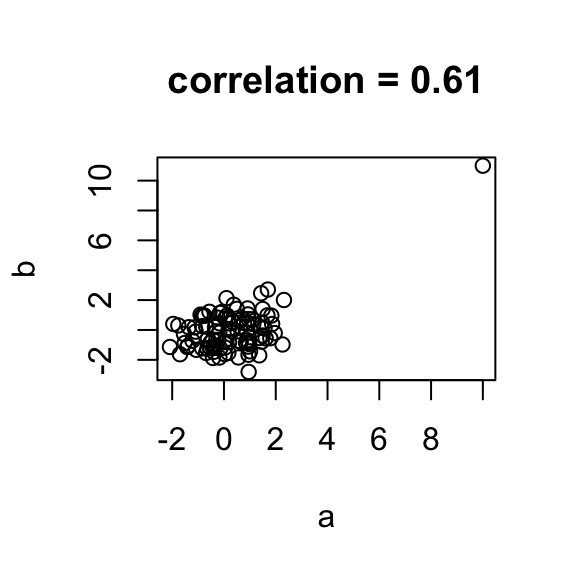

In the example above the data are not associated but for one pair both values are very large. The correlation here is about 0.5. This is driven by just that one point. An alternative summary for cases with outliers or extreme values is **Spearman's correlation** which is based on ranks instead of the values themselves. 

Spearman correlation is robust to outliers. For this example, I created two independent data sets, both with mean 0 and standard deviation 1, independent from each other. So, there is no correlation between the two data sets. And then I made a mistake in one row where both measurements became big.

x=rnorm(100)
y=rnorm(100)
plot(x, y)
#Make a mistake on row 10
x[10]=100
y[10]=100
plot(x, y)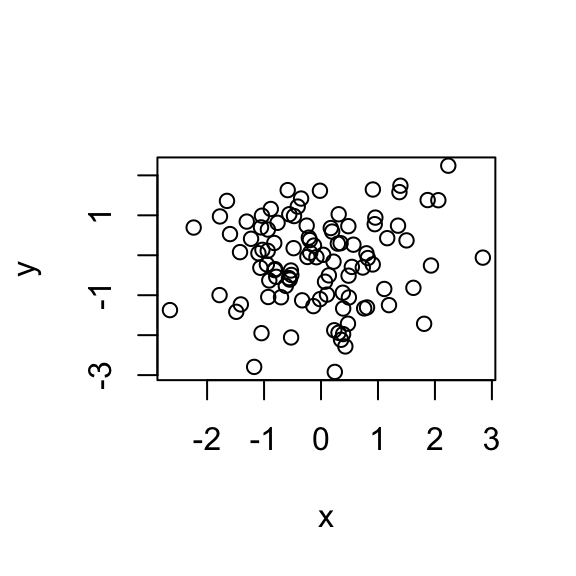

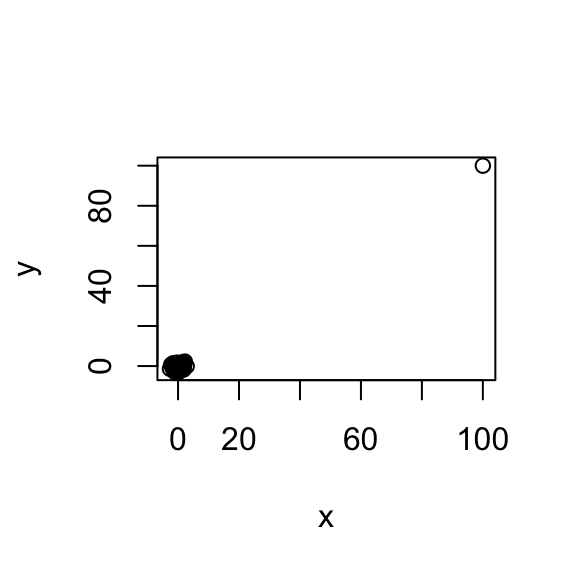
The computed correlation is `r cor(x, y) which is so big because of the extreme point driving the correlation to be high. Spearman correlation is a very simple idea. Instead of looking at the values, we look at the ranks. Instead of plotting the values, I’m plotting the ranks.

rankX=match(x, sort(x))
rankY=match(y, sort(y))
#plot of the ranks
plot(rankX, rankY)
#correlation
cor(rankX, rankY)

## [1] 0.07182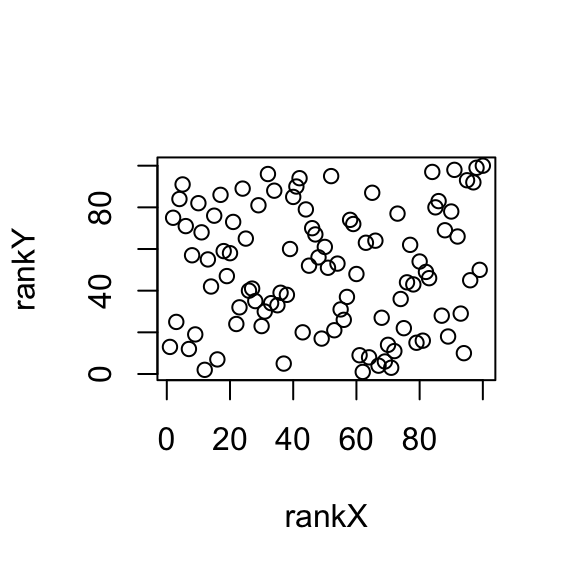

The correlation computed on the ranks is just 0.0718, much closer to the correct answer, which is 0 here. That’s Spearman correlation. When we say robust, we mean it doesn’t affect the measurement so much.

An easy way to run spearman rank correlation is :

#possible values for method : "pearson", "kendall", "spearman"
#see ?cor
cor(x, y, method="spearman")

## [1] 0.07182

Median and MAD

Median and MAD are another robust summary statistics. Let’s start with a very simple illustration to understand this concept. I randomly generated 100 data points from a normal distribution with mean 0 and standard deviation 1. And then I made a mistake on one of the measurements and it turned into 100.

x<-rnorm(100)
x[10]=100
boxplot(x)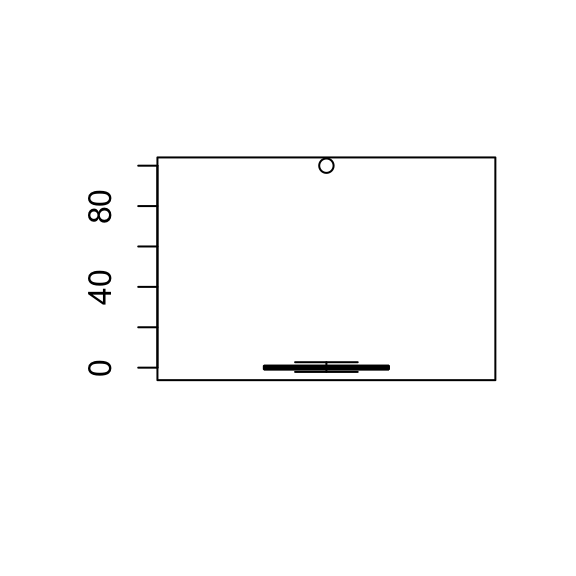

So you can see on the boxplot that one point is extremely high compared to the others and way up at 100. Points like this are called outliers in statistics and are common in high throughput measurement. This one point is going to have a big influence on the sample mean and the standard deviation. The new mean of the modified x values is 0.9323 and the new standard deviation (SD) is 10.0543 which are very different to the original mean and SD.

One summary statistic that isn’t sensitive to outliers is the median. The median is simply the middle point of the data. In this case, the median is -0.0207 which are pretty close to 0 and the MAD, which I’m going to describe next is 1.0309, which is pretty close to 1.

median(x)

## [1] -0.02073

mad(x)

## [1] 1.031

What is the MAD? The MAD (median absolute deviation) is a robust estimate of the standard deviation. MAD is computed as the following formula:

\[ MAD = 1.4826 * median\{|X_i - median(X_i)|\} \]

We compute the median of our samples and then we compute the distance of each point to the median as the absolute value of the difference. Then we take the median of those deviations. that’s where the name comes median absolute deviation, MAD. This value is multiplied by the factor 1.4826, to make the summary statistic unbiased. On average, it’s going to be equal to the standard deviation.

So why do we ever use the average, the standard deviation, and Pearson's correlation? In genomics data where outliers are common, the median, the MAD, and other robust statistics are usually preferable. However, there are cases where using robust statistics actually makes our analysis less sensitive to finding real differences.

Log transformation

When look at microarray or sequencing data, we can compute the mean across samples and the variance across samples. We usually see a relationship between the average and the standard deviation. The higher the average, the higher the standard deviation. So, For highly expressed gene, we have high standard deviations. This can be easily seen by making the log-log plot of the SD according to the average.

A problem is that simple summary statistics like the average are going to be driven by the variance of these very, very highly expressed genes. One simple approach to solve this problem is to take the log of the data for computing the average and the SD across samples. After log transformation, mean-variance relationship is much more flat, which is more desirable. Now we have high expressed genes having about the same variance as most genes.

Log transormation helps to stabilize the variance/mean relationship. Another reason to use logs, is the symetry of log ratios. For example, 2-fold gene overexpression and 2-fold gene underexpression are represented by 1 and -1 in log2 scale in contrast of 2 and 0.5 in linear scale.

Normal approximation and standard unit

Normal distribution is also called the bell curve or Gaussian distribution. the formula is shown below:

\[ \mbox{Pr}(a < x < b) = \int_a^b \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( \frac{-(x-\mu)^2}{2 \sigma^2} \right)} \, dx \]

It tells us that the proportion of numbers between a and b is given by this integral. Here \(\mu\) and \(\sigma\) are refereed to as the mean and standard deviation. Those are the only two numbers we need to know in the case of normal distribution and we can answer the question, what proportion of x is there between any a and any b? For example, you’re going to know that 95% of your data is within two standard deviations of the average. You’re going to know that 99% of your data is within 2.5 standard deviations of the average. 68% are within one standard deviation from the average.

To look whether the data is normally distributed, we can look at what is called a quantile-quantile plot. We have to compute the percentiles. So we go 1%, 2%, 3%. So we compute, what is the number for which 1% of the data is below that number? 2%, 3%, 4%, and we compute what are called the percentiles.We do that for our data set, and we also do that for the normal distribution. The percentiles of normal distribution (y-axis) is plotted according to the percentiles of our data (x-axis). If these two have the same distribution, then these points should fall on the identity line, and in this case they are pretty close. So this is telling us that this is a pretty good approximation.

Standard units is a very useful concept. If you know your data is approximately normal, then you can convert it to what are called standard units, by subtracting the mean and dividing by the standard deviation for each point in your distribution. Those are now going to have normal distribution with mean 0 and standard deviation 1. The value means, how many standard deviations away am I from the mean? If we have a 2, it is a big number, because if it’s normally distributed, only 5% of the data is more than two standard deviations away from the mean.

In summary, if your data is approximated by the normal distribution, then all you need to know about your data is the mean and standard deviation. With those two numbers, you can describe the proportion of any interval.
In other cases, for example gene expression without taking the log. The mean and standard deviation can't be considered summaries in the same way. They may be useful for certain calculations, but they will not be summaries of the data in the same way as they are when the data is normally distributed.

Licence

Licence

References

https://github.com/genomicsclass

Recommended for you