Chi-Square Test of Independence in R

Contents
Data format: Contingency tables
We’ll use housetasks data sets from STHDA: https://www.sthda.com/sthda/RDoc/data/housetasks.txt.
# Import the data
file_path <- "https://www.sthda.com/sthda/RDoc/data/housetasks.txt"
housetasks <- read.delim(file_path, row.names = 1)
# head(housetasks)An image of the data is displayed below:
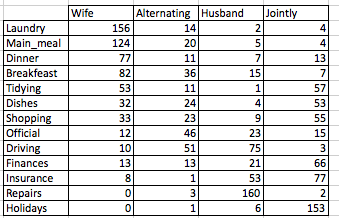
Data format correspondence analysis
The data is a contingency table containing 13 housetasks and their distribution in the couple:
- rows are the different tasks
- values are the frequencies of the tasks done :
- by the wife only
- alternatively
- by the husband only
- or jointly
Graphical display of contengency tables
Contingency table can be visualized using the function balloonplot() [in gplots package]. This function draws a graphical matrix where each cell contains a dot whose size reflects the relative magnitude of the corresponding component.
To execute the R code below, you should install the package gplots: install.packages(“gplots”).
library("gplots")
# 1. convert the data as a table
dt <- as.table(as.matrix(housetasks))
# 2. Graph
balloonplot(t(dt), main ="housetasks", xlab ="", ylab="",
label = FALSE, show.margins = FALSE)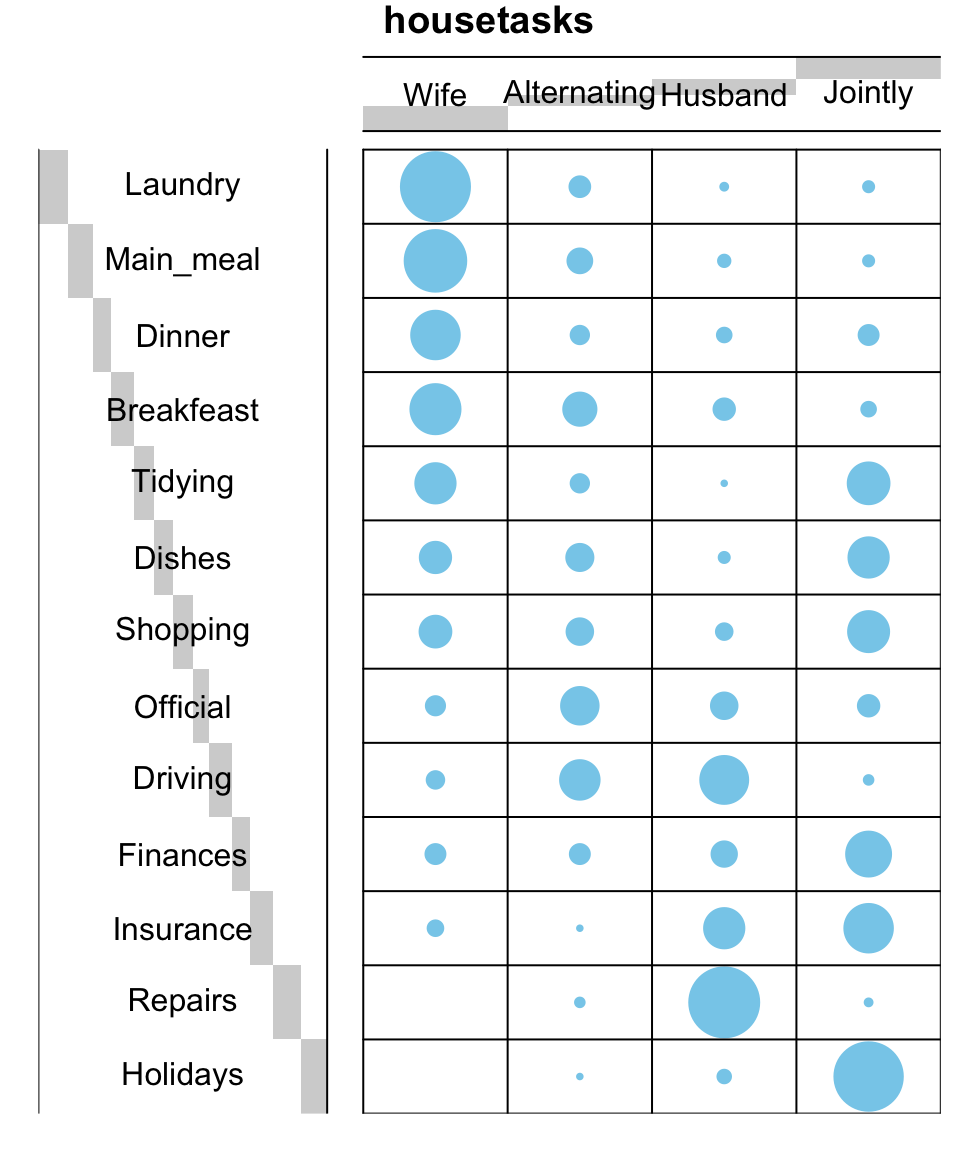
Chi-Square Test of Independence in R
Note that, row and column sums are printed by default in the bottom and right margins, respectively. These values can be hidden using the argument show.margins = FALSE.
It’s also possible to visualize a contingency table as a mosaic plot. This is done using the function mosaicplot() from the built-in R package garphics:
library("graphics")
mosaicplot(dt, shade = TRUE, las=2,
main = "housetasks")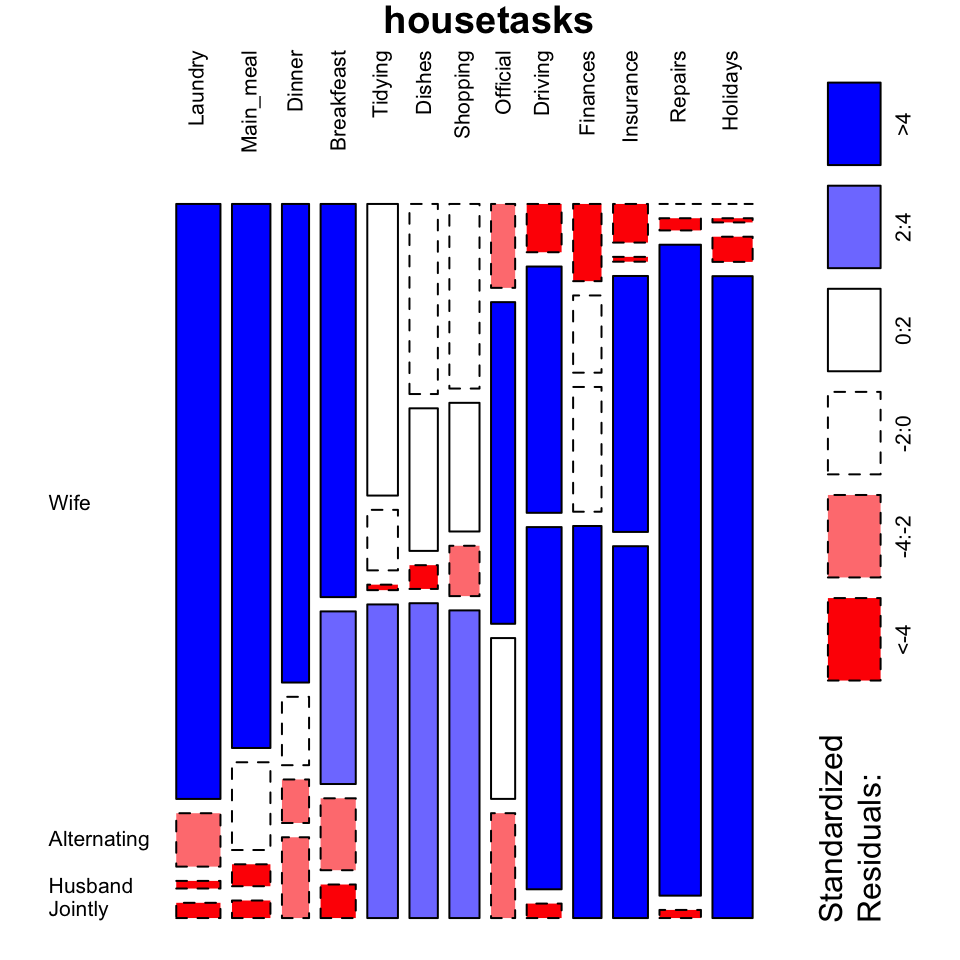
Chi-Square Test of Independence in R
- The argument shade is used to color the graph
- The argument las = 2 produces vertical labels
Note that the surface of an element of the mosaic reflects the relative magnitude of its value.
- Blue color indicates that the observed value is higher than the expected value if the data were random
- Red color specifies that the observed value is lower than the expected value if the data were random
From this mosaic plot, it can be seen that the housetasks Laundry, Main_meal, Dinner and breakfeast (blue color) are mainly done by the wife in our example.
There is another package named vcd, which can be used to make a mosaic plot (function mosaic()) or an association plot (function assoc()).
# install.packages("vcd")
library("vcd")
# plot just a subset of the table
assoc(head(dt, 5), shade = TRUE, las=3)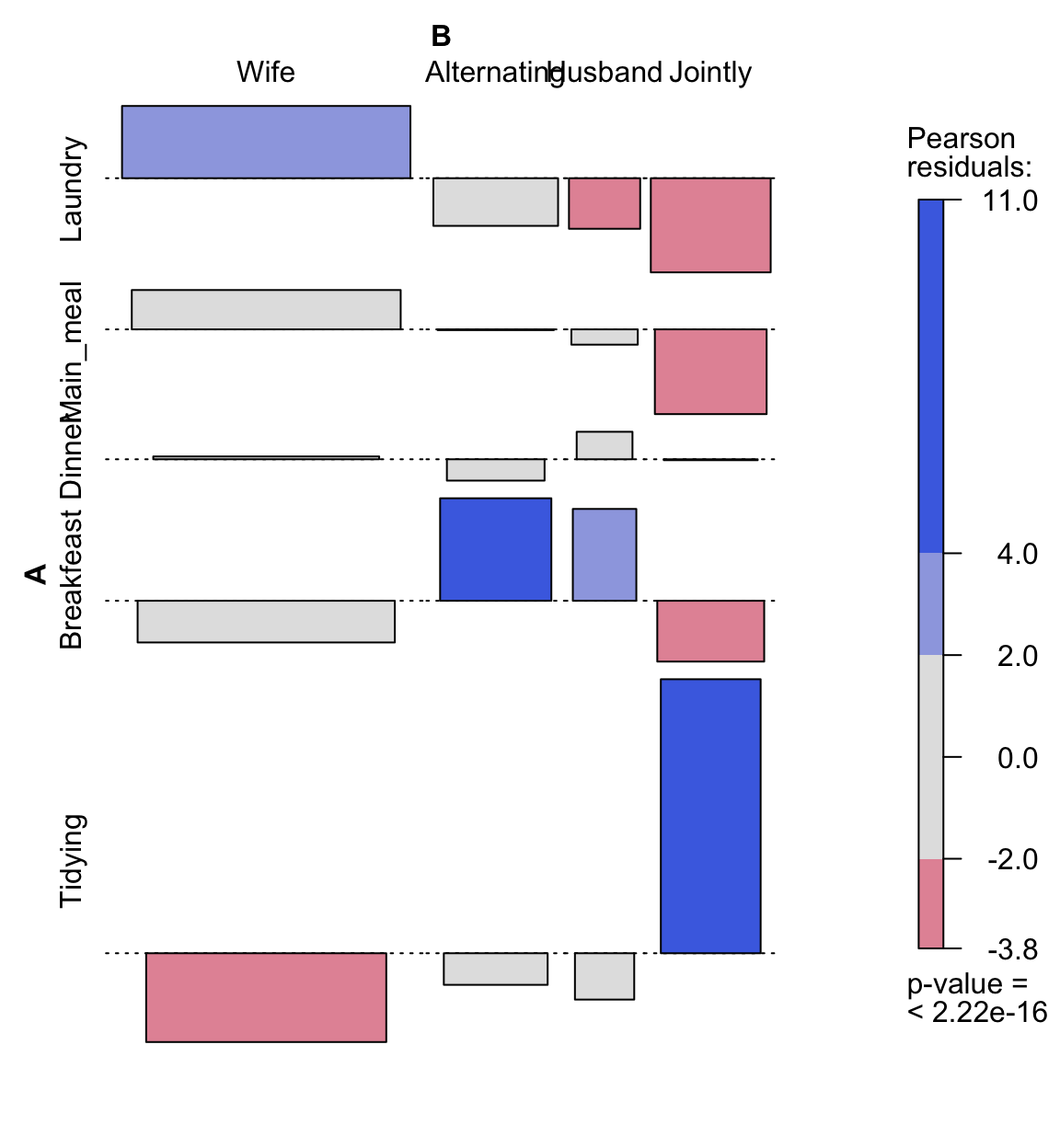
Chi-Square Test of Independence in R
Chi-square test basics
Chi-square test examines whether rows and columns of a contingency table are statistically significantly associated.
- Null hypothesis (H0): the row and the column variables of the contingency table are independent.
- Alternative hypothesis (H1): row and column variables are dependent
For each cell of the table, we have to calculate the expected value under null hypothesis.
For a given cell, the expected value is calculated as follow:
The Chi-square statistic is calculated as follow:
\[ \chi^2 = \sum{\frac{(o - e)^2}{e}} \]
- o is the observed value
- e is the expected value
This calculated Chi-square statistic is compared to the critical value (obtained from statistical tables) with \(df = (r - 1)(c - 1)\) degrees of freedom and p = 0.05.
- r is the number of rows in the contingency table
- c is the number of column in the contingency table
If the calculated Chi-square statistic is greater than the critical value, then we must conclude that the row and the column variables are not independent of each other. This implies that they are significantly associated.
Note that, Chi-square test should only be applied when the expected frequency of any cell is at least 5.
Compute chi-square test in R
Chi-square statistic can be easily computed using the function chisq.test() as follow:
chisq <- chisq.test(housetasks)
chisq
Pearson's Chi-squared test
data: housetasks
X-squared = 1944.5, df = 36, p-value < 2.2e-16In our example, the row and the column variables are statistically significantly associated (p-value = 0).
The observed and the expected counts can be extracted from the result of the test as follow:
# Observed counts
chisq$observed Wife Alternating Husband Jointly
Laundry 156 14 2 4
Main_meal 124 20 5 4
Dinner 77 11 7 13
Breakfeast 82 36 15 7
Tidying 53 11 1 57
Dishes 32 24 4 53
Shopping 33 23 9 55
Official 12 46 23 15
Driving 10 51 75 3
Finances 13 13 21 66
Insurance 8 1 53 77
Repairs 0 3 160 2
Holidays 0 1 6 153# Expected counts
round(chisq$expected,2) Wife Alternating Husband Jointly
Laundry 60.55 25.63 38.45 51.37
Main_meal 52.64 22.28 33.42 44.65
Dinner 37.16 15.73 23.59 31.52
Breakfeast 48.17 20.39 30.58 40.86
Tidying 41.97 17.77 26.65 35.61
Dishes 38.88 16.46 24.69 32.98
Shopping 41.28 17.48 26.22 35.02
Official 33.03 13.98 20.97 28.02
Driving 47.82 20.24 30.37 40.57
Finances 38.88 16.46 24.69 32.98
Insurance 47.82 20.24 30.37 40.57
Repairs 56.77 24.03 36.05 48.16
Holidays 55.05 23.30 34.95 46.70Nature of the dependence between the row and the column variables
As mentioned above the total Chi-square statistic is 1944.456196.
If you want to know the most contributing cells to the total Chi-square score, you just have to calculate the Chi-square statistic for each cell:
\[ r = \frac{o - e}{\sqrt{e}} \]
The above formula returns the so-called Pearson residuals (r) for each cell (or standardized residuals)
Cells with the highest absolute standardized residuals contribute the most to the total Chi-square score.
Pearson residuals can be easily extracted from the output of the function chisq.test():
round(chisq$residuals, 3) Wife Alternating Husband Jointly
Laundry 12.266 -2.298 -5.878 -6.609
Main_meal 9.836 -0.484 -4.917 -6.084
Dinner 6.537 -1.192 -3.416 -3.299
Breakfeast 4.875 3.457 -2.818 -5.297
Tidying 1.702 -1.606 -4.969 3.585
Dishes -1.103 1.859 -4.163 3.486
Shopping -1.289 1.321 -3.362 3.376
Official -3.659 8.563 0.443 -2.459
Driving -5.469 6.836 8.100 -5.898
Finances -4.150 -0.852 -0.742 5.750
Insurance -5.758 -4.277 4.107 5.720
Repairs -7.534 -4.290 20.646 -6.651
Holidays -7.419 -4.620 -4.897 15.556Let’s visualize Pearson residuals using the package corrplot:
library(corrplot)
corrplot(chisq$residuals, is.cor = FALSE)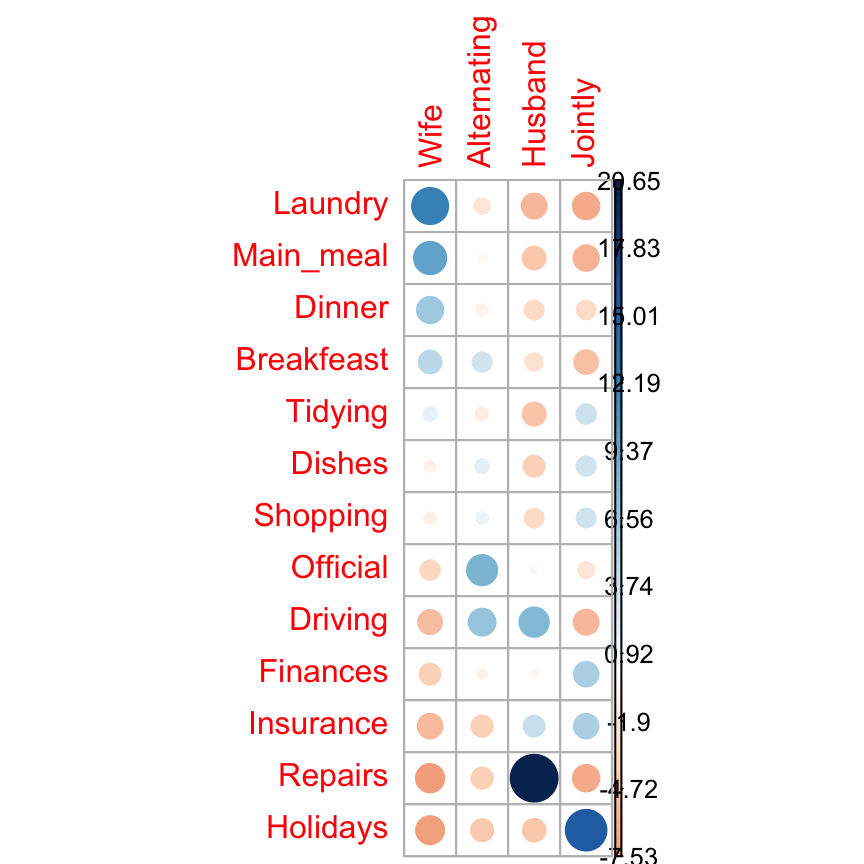
Chi-Square Test of Independence in R
For a given cell, the size of the circle is proportional to the amount of the cell contribution.
The sign of the standardized residuals is also very important to interpret the association between rows and columns as explained in the block below.
- Positive residuals are in blue. Positive values in cells specify an attraction (positive association) between the corresponding row and column variables.
- In the image above, it’s evident that there are an association between the column Wife and the rows Laundry, Main_meal.
- There is a strong positive association between the column Husband and the row Repair
- Negative residuals are in red. This implies a repulsion (negative association) between the corresponding row and column variables. For example the column Wife are negatively associated (~ “not associated”) with the row Repairs. There is a repulsion between the column Husband and, the rows Laundry and Main_meal
The contribution (in %) of a given cell to the total Chi-square score is calculated as follow:
- r is the residual of the cell
# Contibution in percentage (%)
contrib <- 100*chisq$residuals^2/chisq$statistic
round(contrib, 3) Wife Alternating Husband Jointly
Laundry 7.738 0.272 1.777 2.246
Main_meal 4.976 0.012 1.243 1.903
Dinner 2.197 0.073 0.600 0.560
Breakfeast 1.222 0.615 0.408 1.443
Tidying 0.149 0.133 1.270 0.661
Dishes 0.063 0.178 0.891 0.625
Shopping 0.085 0.090 0.581 0.586
Official 0.688 3.771 0.010 0.311
Driving 1.538 2.403 3.374 1.789
Finances 0.886 0.037 0.028 1.700
Insurance 1.705 0.941 0.868 1.683
Repairs 2.919 0.947 21.921 2.275
Holidays 2.831 1.098 1.233 12.445# Visualize the contribution
corrplot(contrib, is.cor = FALSE)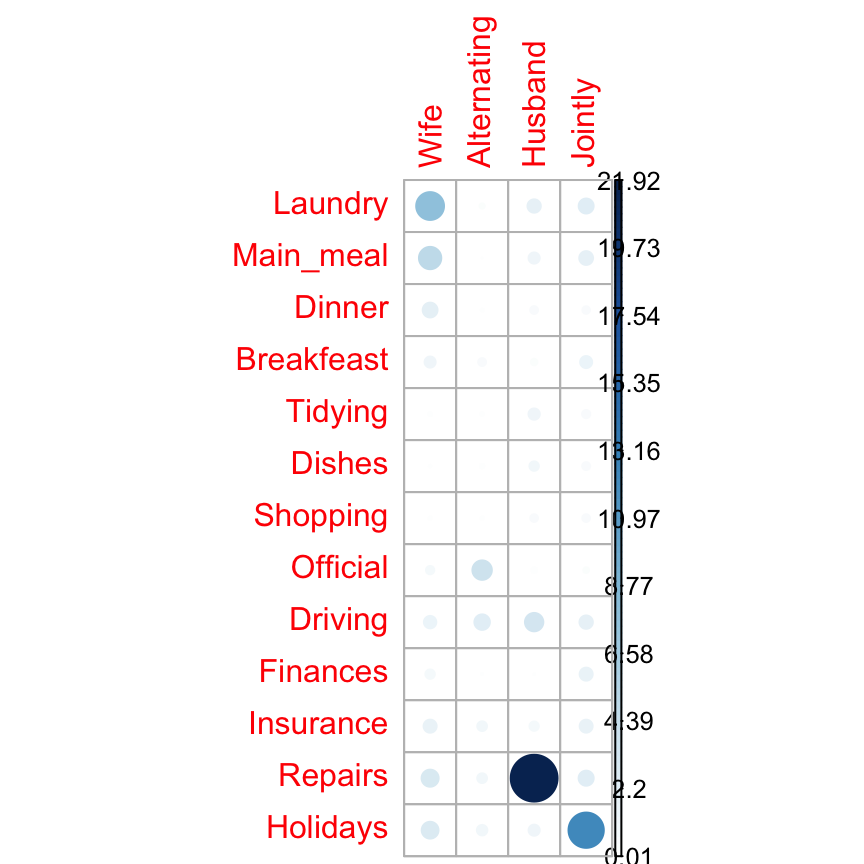
Chi-Square Test of Independence in R
The relative contribution of each cell to the total Chi-square score give some indication of the nature of the dependency between rows and columns of the contingency table.
It can be seen that:
- The column “Wife” is strongly associated with Laundry, Main_meal, Dinner
- The column “Husband” is strongly associated with the row Repairs
- The column jointly is frequently associated with the row Holidays
From the image above, it can be seen that the most contributing cells to the Chi-square are Wife/Laundry (7.74%), Wife/Main_meal (4.98%), Husband/Repairs (21.9%), Jointly/Holidays (12.44%).
These cells contribute about 47.06% to the total Chi-square score and thus account for most of the difference between expected and observed values.
This confirms the earlier visual interpretation of the data. As stated earlier, visual interpretation may be complex when the contingency table is very large. In this case, the contribution of one cell to the total Chi-square score becomes a useful way of establishing the nature of dependency.Access to the values returned by chisq.test() function
The result of chisq.test() function is a list containing the following components:
- statistic: the value the chi-squared test statistic.
- parameter: the degrees of freedom
- p.value: the p-value of the test
- observed: the observed count
- expected: the expected count
The format of the R code to use for getting these values is as follow:
# printing the p-value
chisq$p.value
# printing the mean
chisq$estimateSee also
Infos
This analysis has been performed using R software (ver. 3.2.4).
Show me some love with the like buttons below... Thank you and please don't forget to share and comment below!!
Montrez-moi un peu d'amour avec les like ci-dessous ... Merci et n'oubliez pas, s'il vous plaît, de partager et de commenter ci-dessous!
Recommended for You!
Recommended for you
This section contains the best data science and self-development resources to help you on your path.
Books - Data Science
Our Books
- Practical Guide to Cluster Analysis in R by A. Kassambara (Datanovia)
- Practical Guide To Principal Component Methods in R by A. Kassambara (Datanovia)
- Machine Learning Essentials: Practical Guide in R by A. Kassambara (Datanovia)
- R Graphics Essentials for Great Data Visualization by A. Kassambara (Datanovia)
- GGPlot2 Essentials for Great Data Visualization in R by A. Kassambara (Datanovia)
- Network Analysis and Visualization in R by A. Kassambara (Datanovia)
- Practical Statistics in R for Comparing Groups: Numerical Variables by A. Kassambara (Datanovia)
- Inter-Rater Reliability Essentials: Practical Guide in R by A. Kassambara (Datanovia)
Others
- R for Data Science: Import, Tidy, Transform, Visualize, and Model Data by Hadley Wickham & Garrett Grolemund
- Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems by Aurelien Géron
- Practical Statistics for Data Scientists: 50 Essential Concepts by Peter Bruce & Andrew Bruce
- Hands-On Programming with R: Write Your Own Functions And Simulations by Garrett Grolemund & Hadley Wickham
- An Introduction to Statistical Learning: with Applications in R by Gareth James et al.
- Deep Learning with R by François Chollet & J.J. Allaire
- Deep Learning with Python by François Chollet
Click to follow us on Facebook :
Comment this article by clicking on "Discussion" button (top-right position of this page)







