Penalized Logistic Regression Essentials in R: Ridge, Lasso and Elastic Net
When you have multiple variables in your logistic regression model, it might be useful to find a reduced set of variables resulting to an optimal performing model (see Chapter @ref(penalized-regression)).
Penalized logistic regression imposes a penalty to the logistic model for having too many variables. This results in shrinking the coefficients of the less contributive variables toward zero. This is also known as regularization.
The most commonly used penalized regression include:
- ridge regression: variables with minor contribution have their coefficients close to zero. However, all the variables are incorporated in the model. This is useful when all variables need to be incorporated in the model according to domain knowledge.
- lasso regression: the coefficients of some less contributive variables are forced to be exactly zero. Only the most significant variables are kept in the final model.
- elastic net regression: the combination of ridge and lasso regression. It shrinks some coefficients toward zero (like ridge regression) and set some coefficients to exactly zero (like lasso regression)
This chapter describes how to compute penalized logistic regression, such as lasso regression, for automatically selecting an optimal model containing the most contributive predictor variables.
Contents:
Loading required R packages
tidyversefor easy data manipulation and visualizationcaretfor easy machine learning workflowglmnet, for computing penalized regression
library(tidyverse)
library(caret)
library(glmnet)Preparing the data
Data set: PimaIndiansDiabetes2 [in mlbench package], introduced in Chapter @ref(classification-in-r), for predicting the probability of being diabetes positive based on multiple clinical variables.
We’ll randomly split the data into training set (80% for building a predictive model) and test set (20% for evaluating the model). Make sure to set seed for reproductibility.
# Load the data and remove NAs
data("PimaIndiansDiabetes2", package = "mlbench")
PimaIndiansDiabetes2 <- na.omit(PimaIndiansDiabetes2)
# Inspect the data
sample_n(PimaIndiansDiabetes2, 3)
# Split the data into training and test set
set.seed(123)
training.samples <- PimaIndiansDiabetes2$diabetes %>%
createDataPartition(p = 0.8, list = FALSE)
train.data <- PimaIndiansDiabetes2[training.samples, ]
test.data <- PimaIndiansDiabetes2[-training.samples, ]Computing penalized logistic regression
Additionnal data preparation
The R function model.matrix() helps to create the matrix of predictors and also automatically converts categorical predictors to appropriate dummy variables, which is required for the glmnet() function.
# Dumy code categorical predictor variables
x <- model.matrix(diabetes~., train.data)[,-1]
# Convert the outcome (class) to a numerical variable
y <- ifelse(train.data$diabetes == "pos", 1, 0)R functions
We’ll use the R function glmnet() [glmnet package] for computing penalized logistic regression.
The simplified format is as follow:
glmnet(x, y, family = "binomial", alpha = 1, lambda = NULL)x: matrix of predictor variablesy: the response or outcome variable, which is a binary variable.family: the response type. Use “binomial” for a binary outcome variablealpha: the elasticnet mixing parameter. Allowed values include:- “1”: for lasso regression
- “0”: for ridge regression
- a value between 0 and 1 (say 0.3) for elastic net regression.
lamba: a numeric value defining the amount of shrinkage. Should be specify by analyst.
In penalized regression, you need to specify a constant lambda to adjust the amount of the coefficient shrinkage. The best lambda for your data, can be defined as the lambda that minimize the cross-validation prediction error rate. This can be determined automatically using the function cv.glmnet().
In the following R code, we’ll show how to compute lasso regression by specifying the option alpha = 1. You can also try the ridge regression, using alpha = 0, to see which is better for your data.
Quick start R code
Fit the lasso penalized regression model:
library(glmnet)
# Find the best lambda using cross-validation
set.seed(123)
cv.lasso <- cv.glmnet(x, y, alpha = 1, family = "binomial")
# Fit the final model on the training data
model <- glmnet(x, y, alpha = 1, family = "binomial",
lambda = cv.lasso$lambda.min)
# Display regression coefficients
coef(model)
# Make predictions on the test data
x.test <- model.matrix(diabetes ~., test.data)[,-1]
probabilities <- model %>% predict(newx = x.test)
predicted.classes <- ifelse(probabilities > 0.5, "pos", "neg")
# Model accuracy
observed.classes <- test.data$diabetes
mean(predicted.classes == observed.classes)Compute lasso regression
Find the optimal value of lambda that minimizes the cross-validation error:
library(glmnet)
set.seed(123)
cv.lasso <- cv.glmnet(x, y, alpha = 1, family = "binomial")
plot(cv.lasso)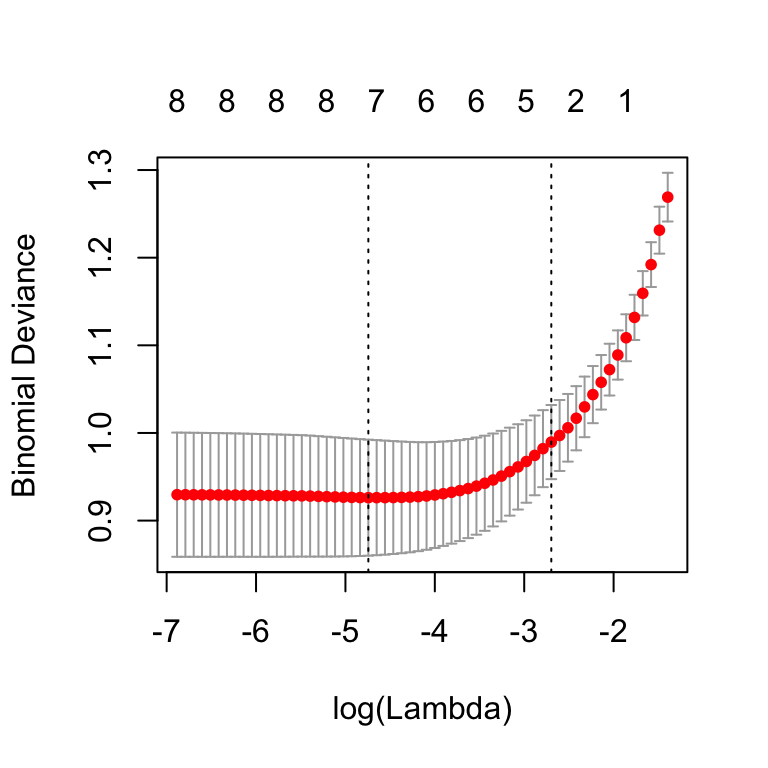
The plot displays the cross-validation error according to the log of lambda. The left dashed vertical line indicates that the log of the optimal value of lambda is approximately -5, which is the one that minimizes the prediction error. This lambda value will give the most accurate model. The exact value of lambda can be viewed as follow:
cv.lasso$lambda.min## [1] 0.00871Generally, the purpose of regularization is to balance accuracy and simplicity. This means, a model with the smallest number of predictors that also gives a good accuracy. To this end, the function cv.glmnet() finds also the value of lambda that gives the simplest model but also lies within one standard error of the optimal value of lambda. This value is called lambda.1se.
cv.lasso$lambda.1se## [1] 0.0674Using lambda.min as the best lambda, gives the following regression coefficients:
coef(cv.lasso, cv.lasso$lambda.min)## 9 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) -8.615615
## pregnant 0.035076
## glucose 0.036916
## pressure .
## triceps 0.016484
## insulin -0.000392
## mass 0.030485
## pedigree 0.785506
## age 0.036265
From the output above, only the viable triceps has a coefficient exactly equal to zero.
Using lambda.1se as the best lambda, gives the following regression coefficients:
coef(cv.lasso, cv.lasso$lambda.1se)## 9 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) -4.65750
## pregnant .
## glucose 0.02628
## pressure .
## triceps 0.00191
## insulin .
## mass .
## pedigree .
## age 0.01734
Using lambda.1se, only 5 variables have non-zero coefficients. The coefficients of all other variables have been set to zero by the lasso algorithm, reducing the complexity of the model.
Setting lambda = lambda.1se produces a simpler model compared to lambda.min, but the model might be a little bit less accurate than the one obtained with lambda.min.
In the next sections, we’ll compute the final model using lambda.min and then assess the model accuracy against the test data. We’ll also discuss the results obtained by fitting the model using lambda = lambda.1se.
Compute the final lasso model:
- Compute the final model using
lambda.min:
# Final model with lambda.min
lasso.model <- glmnet(x, y, alpha = 1, family = "binomial",
lambda = cv.lasso$lambda.min)
# Make prediction on test data
x.test <- model.matrix(diabetes ~., test.data)[,-1]
probabilities <- lasso.model %>% predict(newx = x.test)
predicted.classes <- ifelse(probabilities > 0.5, "pos", "neg")
# Model accuracy
observed.classes <- test.data$diabetes
mean(predicted.classes == observed.classes)## [1] 0.769- Compute the final model using
lambda.1se:
# Final model with lambda.1se
lasso.model <- glmnet(x, y, alpha = 1, family = "binomial",
lambda = cv.lasso$lambda.1se)
# Make prediction on test data
x.test <- model.matrix(diabetes ~., test.data)[,-1]
probabilities <- lasso.model %>% predict(newx = x.test)
predicted.classes <- ifelse(probabilities > 0.5, "pos", "neg")
# Model accuracy rate
observed.classes <- test.data$diabetes
mean(predicted.classes == observed.classes)## [1] 0.705In the next sections, we’ll compare the accuracy obtained with lasso regression against the one obtained using the full logistic regression model (including all predictors).
Compute the full logistic model
# Fit the model
full.model <- glm(diabetes ~., data = train.data, family = binomial)
# Make predictions
probabilities <- full.model %>% predict(test.data, type = "response")
predicted.classes <- ifelse(probabilities > 0.5, "pos", "neg")
# Model accuracy
observed.classes <- test.data$diabetes
mean(predicted.classes == observed.classes)## [1] 0.808Discussion
This chapter described how to compute penalized logistic regression model in R. Here, we focused on lasso model, but you can also fit the ridge regression by using alpha = 0 in the glmnet() function. For elastic net regression, you need to choose a value of alpha somewhere between 0 and 1. This can be done automatically using the caret package. See Chapter @ref(penalized-regression).
Our analysis demonstrated that the lasso regression, using lambda.min as the best lambda, results to simpler model without compromising much the model performance on the test data when compared to the full logistic model.
The model accuracy that we have obtained with lambda.1se is a bit less than what we got with the more complex model using all predictor variables (n = 8) or using lambda.min in the lasso regression. Even with lambda.1se, the obtained accuracy remains good enough in addition to the resulting model simplicity.
This means that the simpler model obtained with lasso regression does at least as good a job fitting the information in the data as the more complicated one. According to the bias-variance trade-off, all things equal, simpler model should be always preferred because it is less likely to overfit the training data.
For variable selection, an alternative to the penalized logistic regression techniques is the stepwise logistic regression described in the Chapter @ref(stepwise-logistic-regression).



