How to choose the appropriate clustering algorithms for your data? - Unsupervised Machine Learning

This article has been updated, you are now consulting an old release of this article!


There are many clustering algorithms published in the literature, including:

For a given dataset, choosing the appropriate clustering method and the optimal number of clusters can be a hard task for the analyst.

As described in two of my previous articles(determining the optimal number of clusters and cluster validation statistics), there are more than 30 indices for assessing the goodness of clustering results and for identify the best performing clustering algorithm for a particular dataset.


This article describes the R package clValid (G. Brock et al., 2008) which can be used for simultaneously comparing multiple clustering algorithms in a single function call for identifying the best clustering approach and the optimal number of clusters.


The package clValid contains 3 different types of clustering validation measures:

  • Clustering internal validation, which uses intrinsic information in the data to assess the quality of the clustering.
  • Clustering stability validation, which is a special version of internal validation. It evaluates the consistency of a clustering result by comparing it with the clusters obtained after each column is removed, one at a time.
  • Clustering biological validation, which evaluates the ability of a clustering algorithm to produce biologically meaningful clusters.

We’ll start by describing the different clustering validation measures in the package. Next, we’ll present the function clValid() and finally we’ll provide an R lab section for validating clustering results and comparing clustering algorithms.

1 Clustering validation measures in clValid package

1.1 Internal validation measures

The internal measures included in clValid package are:

  1. Connectivity
  2. Average Silhouette width
  3. Dunn index

These methods has been already described in my previous article: clustering validation statistic.

Briefly, connectivity indicates the degree of connectedness of the clusters, as determined by k-nearest neighbors. Connectedness corresponds to what extent items are placed in the same cluster as their nearest neighbors in the data space. The connectivity has a value between 0 and infinity and should be minimized.

Silhouette width and Dunn index combine measures of compactness and separation of the clusters. Recall that the values of silhouette width range from -1 (poorly clustered observations) to 1 (well clustered observations). The Dunn index is the ratio between the smallest distance between observations not in the same cluster to the largest intra-cluster distance. It has a value between 0 and infinity and should be maximized.

1.2 Stability validation measures

The cluster stability measures includes:

  • The average proportion of non-overlap (APN)
  • The average distance (AD)
  • The average distance between means (ADM)
  • The figure of merit (FOM)

The APN, AD, and ADM are all based on the cross-classification table of the original clustering with the clustering based on the removal of one column.

  • The APN measures the average proportion of observations not placed in the same cluster by clustering based on the full data and clustering based on the data with a single column removed.

  • The AD measures the average distance between observations placed in the same cluster under both cases (full dataset and removal of one column).

  • The ADM measures the average distance between cluster centers for observations placed in the same cluster under both cases.

  • The FOM measures the average intra-cluster variance of the deleted column, where the clustering is based on the remaining (undeleted) columns. It also has a value between zero and 1, and again smaller values are preferred.

The values of APN, ADM and FOM ranges from 0 to 1, with smaller value corresponding with highly consistent clustering results. AD has a value between 0 and infinity, and smaller values are also preferred.

1.3 Biological validation measures

Biological validation evaluates the ability of a clustering algorithm to produce biologically meaningful clusters. An application is microarray or RNAseq data where observations corresponds to genes.

There are two biological measures:

  • The biological homogeneity index (BHI)
  • The biological stability index (BSI)

The BHI measures the average proportion of gene pairs that are clustered together which have matching biological functional classes.

The BSI is similar to the other stability measures, but inspects the consistency of clustering for genes with similar biological functionality. Each sample is removed one at a time, and the cluster membership for genes with similar functional annotation is compared with the cluster membership using all available samples.

2 R function clValid()

2.1 Format

The main function in clValid package is clValid():

clValid(obj, nClust, clMethods = "hierarchical",
        validation = "stability", maxitems = 600,
        metric = "euclidean", method = "average")

  • obj: A numeric matrix or data frame. Rows are the items to be clustered and columns are samples.
  • nClust: A numeric vector specifying the numbers of clusters to be evaluated. e.g., 2:10
  • clMethods: The clustering method to be used. Available options are “hierarchical”, “kmeans”, “diana”, “fanny”, “som”, “model”, “sota”, “pam”, “clara”, and “agnes”, with multiple choices allowed.
  • validation: The type of validation measures to be used. Allowed values are “internal”, “stability”, and “biological”, with multiple choices allowed.
  • maxitems: The maximum number of items (rows in matrix) which can be clustered.
  • metric: The metric used to determine the distance matrix. Possible choices are “euclidean”, “correlation”, and “manhattan”.
  • method: For hierarchical clustering (hclust and agnes), the agglomeration method to be used. Available choices are “ward”, “single”, “complete” and “average”.


2.2 Examples of usage

2.2.1 Data

We’ll use mouse data [in clValid package ] which is an Affymetrix gene expression data of of mesenchymal cells from two distinct lineages (M and N). It contains 147 genes and 6 samples (3 samples for each lineage).

library(clValid)
# Load the data
data(mouse)
head(mouse)
##             ID       M1       M2       M3      NC1      NC2      NC3
## 1   1448995_at 4.706812 4.528291 4.325836 5.568435 6.915079 7.353144
## 2 1436392_s_at 3.867962 4.052354 3.474651 4.995836 5.056199 5.183585
## 3 1437434_a_at 2.875112 3.379619 3.239800 3.877053 4.459629 4.850978
## 4   1428922_at 5.326943 5.498930 5.629814 6.795194 6.535522 6.622577
## 5 1452671_s_at 5.370125 4.546810 5.704810 6.407555 6.310487 6.195847
## 6   1448147_at 3.471347 4.129992 3.964431 4.474737 5.185631 5.177967
##                       FC
## 1 Growth/Differentiation
## 2   Transcription factor
## 3          Miscellaneous
## 4          Miscellaneous
## 5          ECM/Receptors
## 6 Growth/Differentiation
# Extract gene expression data
exprs <- mouse[1:25,c("M1","M2","M3","NC1","NC2","NC3")]
rownames(exprs) <- mouse$ID[1:25]
head(exprs)
##                    M1       M2       M3      NC1      NC2      NC3
## 1448995_at   4.706812 4.528291 4.325836 5.568435 6.915079 7.353144
## 1436392_s_at 3.867962 4.052354 3.474651 4.995836 5.056199 5.183585
## 1437434_a_at 2.875112 3.379619 3.239800 3.877053 4.459629 4.850978
## 1428922_at   5.326943 5.498930 5.629814 6.795194 6.535522 6.622577
## 1452671_s_at 5.370125 4.546810 5.704810 6.407555 6.310487 6.195847
## 1448147_at   3.471347 4.129992 3.964431 4.474737 5.185631 5.177967

2.2.2 Compute clValid()

We start by internal cluster validation which measures the connectivity, silhouette width and Dunn index. It’s possible to compute simultaneously these internal measures for multiple clustering algorithms in combination with a range of cluster numbers. The R code below can be used:

# Compute clValid
clmethods <- c("hierarchical","kmeans","pam")
intern <- clValid(exprs, nClust = 2:6,
              clMethods = clmethods, validation = "internal")
# Summary
summary(intern)
##
## Clustering Methods:
##  hierarchical kmeans pam
##
## Cluster sizes:
##  2 3 4 5 6
##
## Validation Measures:
##                                  2       3       4       5       6
##
## hierarchical Connectivity   4.6159 11.5865 19.5075 22.2075 24.5044
##              Dunn           0.4217  0.2315  0.3068  0.3456  0.3456
##              Silhouette     0.5997  0.4529  0.4324  0.4007  0.3891
## kmeans       Connectivity   4.6159  9.5607 20.4774 23.1774 26.2242
##              Dunn           0.4217  0.3924  0.1360  0.1556  0.1778
##              Silhouette     0.5997  0.5495  0.4235  0.3871  0.3618
## pam          Connectivity   4.6159  9.5607 18.5925 25.0631 31.8381
##              Dunn           0.4217  0.3924  0.3068  0.3068  0.2511
##              Silhouette     0.5997  0.5495  0.4401  0.4297  0.3506
##
## Optimal Scores:
##
##              Score  Method       Clusters
## Connectivity 4.6159 hierarchical 2
## Dunn         0.4217 hierarchical 2
## Silhouette   0.5997 hierarchical 2

It can be seen that hierarchical clustering with two clusters performs the best in each case (i.e., for connectivity, Dunn and Silhouette measures).

The plots of the connectivity, Dunn index, and silhouette width can be generated as follow:

plot(intern)

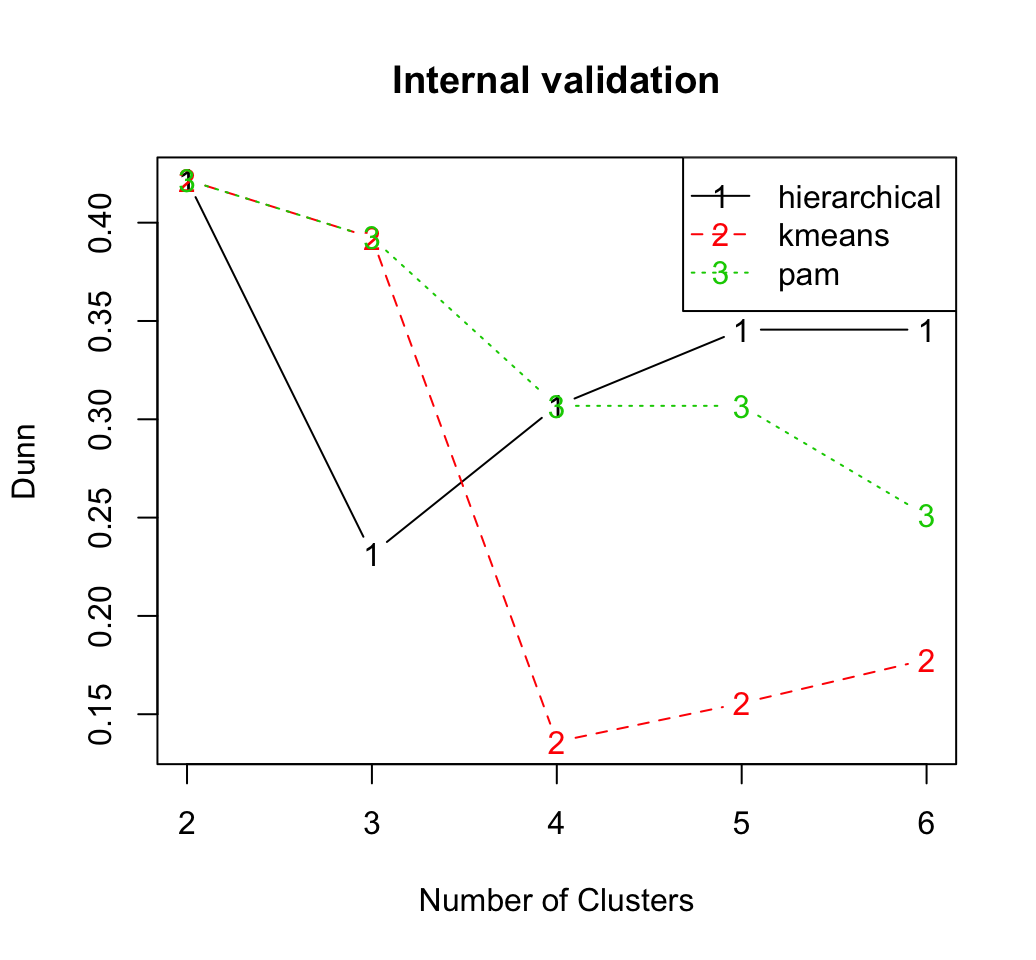
clValid - Unsupervised Machine LearningclValid - Unsupervised Machine LearningclValid - Unsupervised Machine Learning

Recall that the connectivity should be minimized, while both the Dunn index and the silhouette width should be maximized.

Thus, it appears that hierarchical clustering outperforms the other clustering algorithms under each validation measure, for nearly every number of clusters evaluated.

Regardless of the clustering algorithm, the optimal number of clusters seems to be two using the three measures.

Stability measures can be computed as follow:

# Stability measures
clmethods <- c("hierarchical","kmeans","pam")
stab <- clValid(exprs, nClust = 2:6, clMethods = clmethods,
                validation = "stability")
# Display only optimal Scores
optimalScores(stab)
##         Score       Method Clusters
## APN 0.0000000 hierarchical        2
## AD  0.9642344          pam        6
## ADM 0.0000000 hierarchical        2
## FOM 0.3925939          pam        6

It’s also possible to display a complete summary:

summary(stab)
plot(stab)

For the APN and ADM measures, hierarchical clustering with two clusters again gives the best score. For the other measures, PAM with six clusters has the best score.

For cluster biological validation read the documentation of clValid() (?clValid).

3 Infos

This analysis has been performed using R software (ver. 3.2.1)

  • Brock, G., Pihur, V., Datta, S. and Datta, S. (2008) clValid: An R Package for Cluster Validation Journal of Statistical Software 25(4) http://www.jstatsoft.org/v25/i04

Enjoyed this article? I’d be very grateful if you’d help it spread by emailing it to a friend, or sharing it on Twitter, Facebook or Linked In.

Show me some love with the like buttons below... Thank you and please don't forget to share and comment below!!
Avez vous aimé cet article? Je vous serais très reconnaissant si vous aidiez à sa diffusion en l'envoyant par courriel à un ami ou en le partageant sur Twitter, Facebook ou Linked In.

Montrez-moi un peu d'amour avec les like ci-dessous ... Merci et n'oubliez pas, s'il vous plaît, de partager et de commenter ci-dessous!