Test t de Student

Probablement l?une des questions les plus populaires dans le domaine de la recherche est de savoir si deux groupes d??chantillons ind?pendants diff?rent l?un de l?autre. Le test de Student est l?un des tests statistiques le plus utilis? pour comparer les moyennes de deux groupes ind?pendants ou appari?s.

La formule du test de Student est d?crite en d?tails ici et le test peut ?tre facilement fait en utilisant la fonction t.test() de R. Cependant, une des questions majeures est:

Est il toujours correct de comparer des moyennes?

La r?ponse est bien ?videmment non!! Ceci est expliqu? dans la section suivante.

L?objectif de cet article est :

• Premi?rement, de discuter ? propos des conditions d?utilisation du test de Student
• Deuxi?mement, de fournir une fonction R simple d?utilisation (rquery.t.test()) permettant de guider ?tape par ?tape l?utilisateur dans le but de faire le test de student en respectant les conditions appropri?es d?application.

Conditions d?application du test de Student : Normalit? et ?galit? des variances

Les erreurs statistiques sont fr?quentes dans les articles scientifiques, et environ 50% des articles publi?s contiennent au moins une erreur. Beaucoup de tests statistiques notamment la corr?lation, la r?gression, le test de Student et l?analyse de variance supposent que les donn?es suivent une distribution normale.

Ces tests sont appel?s tests param?triques car leur validit? d?pend de la distribution des donn?es.

Une erreur fr?quente est d?utiliser des tests statistiques qui supposent une distribution normale sur des donn?es qui ne suivent pas la loi normale.

Comme mentionner ci-dessus, on ne peut pas toujours utiliser le test de Student pour comparer des moyennes. Il existe diff?rents types de tests de Student(test-de-student-formules): Le test de Student pour un ?chantillon unique, le test de Student pour ?chantillons ind?pendants et le test de Student pour ?chantillons appari?s.

Ces diff?rents tests peuvent ?tre utilis?s seulement sous certaines conditions :

Ces conditions doivent ?tre v?rifi?es s?rieusement pour pouvoir tirer des conclusions fiables.

Le r?sultat de ces tests pr?liminaires d?termine par la suite la m?thode ? utiliser pour comparer les ?chantillons. Malheureusement, ces pr?-tests ne sont pas automatiquement faits par la fonction native t.test() du logiciel R. C?est la raison pour laquelle j?ai ?crit la fonction rquery.t.test() qui va tout d?abord v?rifier les conditions d?application du test de Student et ensuite d?cide de la m?thode ? utiliser (test param?trique ou non-param?trique) ? partir du r?sultat des tests pr?liminaires.

Comment tester la normalit? des donn?es?

Lorsque la taille des ?chantillons est suffisamment grande (n >30), on peut ignorer le test de normalit? sans probl?me majeur.

Le th?or?me central limite nous dit que, la distribution de l??chantillonnage tend ? suivre la loi normale lorsque la taille est grande ( n > 30).

En revanche, pour ?tre rigoureux, la normalit? peut ?tre v?rifier par une inspection visuelle [Histogramme, Q-Q plot (quantile-quantile plot)] ou par des tests de significativit?.

• L?histogramme permet un jugement visuel ? savoir si la distribution est une courbe en cloche (courbe de Gauss).
• Le test de significativit? compare la distribution d?un ?chantillon donn? ? celle de la loi normale et renvoie une p-value.

Plusieurs m?thodes existent pour le test de normalit?, notamment le test de Kolmogorov-Smirnov (K-S) et le test de Shapiro-Wilk.

L?hypoth?se nulle (H0) de ces tests est : " L??chantillon suit une loi normale?. Si le test est significatif, la distribution ne suit pas une loi normale.

La m?thode de Shapiro-Wilk est le plus largement recommend? pour le test de normalit? et il plus puissant que le test de K-S. Il est bas? sur la corr?lation entre les donn?es et les scores th?oriques de la loi normale.

Notez que le test de normalit? est sensible ? la taille des ?chantillons. Les ?chantillons de petite taille passe tr?s souvent le test de normalit?. Par cons?quent, il est important de combiner une inspection visuelle et un test de significativit? pour prendre la bonne d?cision.

Question : Faire ou ne pas faire le test de normalit??

Le test de normalit? et les autres hypoth?ses faites par les tests param?triques devraient ?tre pr?-test?s avant de continuer avec le test principal de comparaison de moyennes. Par exemple, dans le domaine de la recherche m?dicale, la distribution normale des donn?es est une exception plut?t qu?une r?gle. Dans de telles situations, l?utilisation des tests param?triques n?est pas encourag?e. Les tests non-param?triques, tel que le test de Wilcoxon, sont recommand?s.

Dans la fonction rquery.t.test(), le test de normalit? de Shapiro-Wilk est utilis? et, une histogramme et un Q-Q plot sont automatiquement dessin?s pour une inspection visuelle.

Comment tester l??galit? des variances ?

Le test de Student ind?pendant classique suppose l?homog?n?it? des variances des deux groupes ? comparer. Si les deux ?chantillons suivent une loi normale, le test F peut ?tre utilis? pour comparer les variances.

L?hypoth?se nulle (H0) du test F est : ?les variances des deux groupes sont ?gales?. Si le test est significatif, l?hypoth?se nulle est rejet? et on peut conclure que les variances sont significativement diff?rents.

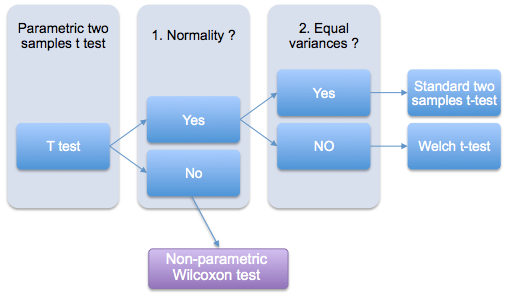
Que faire lorsque les conditions d?application du test de Student ne sont pas remplies?

Si les deux groupes d??chantillons suivent une loi normale, mais de variances in?gales, le test t de Welch peut ?tre utilis? (figure ci-dessous). Le test t de Welch est une adaptation du test t de Student et il est utilis? pour comparer deux ?chantillons lorsque l??galit? des variances ne peut ?tre assum?e.

rquery.t.test : La fonction t.test int?lligente

Comme mentionner ci-dessus, cette fonction est une am?lioration de la fonction native t.test() de R. Elle peut ?tre utilis?e pour faire un test de Student appari? ou ind?pendant. Son avantage est qu?elle v?rifie automatiquement la distribution des donn?es et l??galit? des variances des deux ?chantillons (dans le cas d?un test de Student ind?pendant).

Avant de calculer le t test, la fonction rquery.t.test effectue les ?tapes suivantes :

1. Premi?rement, le test de Shapiro Wilk est utilis? pour effectuer le test de normalit?. Si les donn?es ne suivent pas une loi normale, la fonction rquery.test vous avertira et vous sugg?re de faire le test de Wilcoxon.

2. Un test F de comparaison de variances est ?galement fait automatiquement :

• Si les variances sont consid?r?es ?gales : le test de Student classique est effectu?
• Si les variances sont significativement diff?rentes : le test t de Welch est appliqu?.

Notez que le code R de la fonction rquery.t.test() est fourni ? la fin de ce document.

Un format simplifi? de la fonction est :

rquery.t.test(x, y = NULL, paired = FALSE, graph = TRUE, ...)

Test de Student pour ?chantillon unique : Comparaison d?une moyenne observ?e ? une moyenne th?orique

source('http://www.sthda.com/upload/rquery_t_test.r')
set.seed(123456789)
x<-rnorm(100) # g?n?rer des donn?es
rquery.t.test(x, mu=0)

    One Sample t-test
data:  x
t = 0.2606, df = 99, p-value = 0.7949
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.1657  0.2159
sample estimates:
mean of x 
  0.02506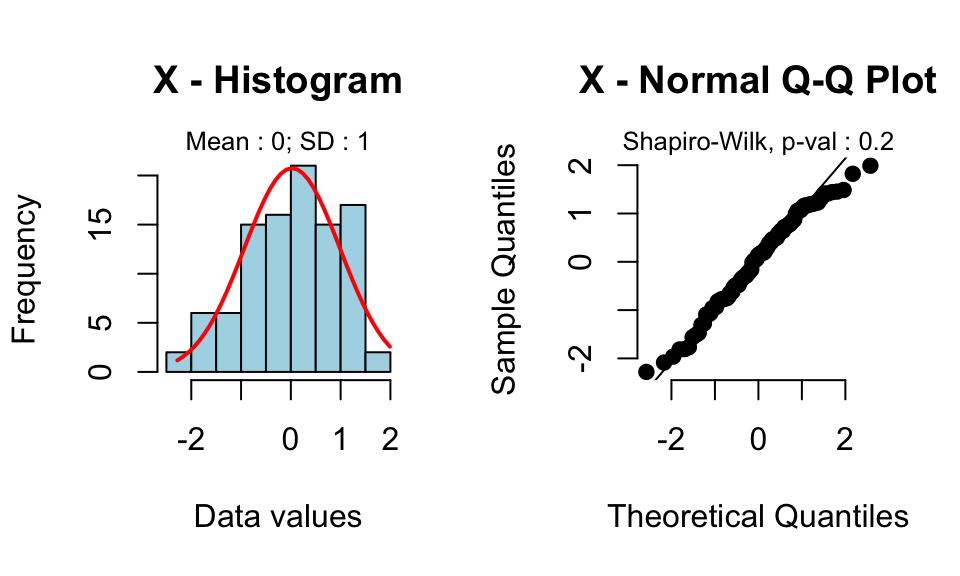 

Lire plus en suivant ce lien : Test de Student pour ?chantillon unique

Test de Student ind?pendant : Comparaison de moyennes de deux groupes d??chantillons ind?pendants

Cas 1 - Les deux groupes d??chantillons suivent des lois normales et sont de variances ?gales:

source('http://www.sthda.com/upload/rquery_t_test.r')
set.seed(123456789)
x<-rnorm(100, mean=2, sd=0.9)
y<-rnorm(100, mean=4, sd=1)
rquery.t.test(x, y)

    Two Sample t-test
data:  x and y
t = -16.85, df = 198, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -2.449 -1.935
sample estimates:
mean of x mean of y 
    2.023     4.215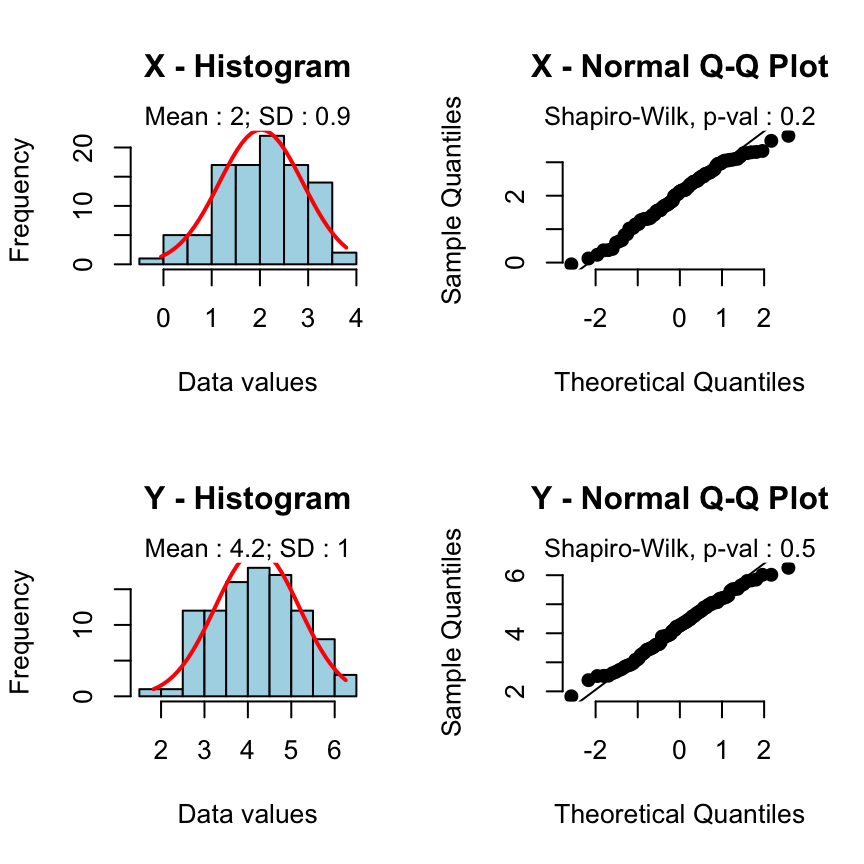 

Le test de Student classique est utilis? automatiquement.

Cas 2 - Les ?chantillons suivent des lois normales mais de variances diff?rentes:

source('http://www.sthda.com/upload/rquery_t_test.r')
set.seed(123456789)
x<-rnorm(100, mean=2, sd=0.9)
y<-rnorm(100, mean=2, sd=3)
rquery.t.test(x, y)

    Welch Two Sample t-test
data:  x and y
t = -2.043, df = 116.3, p-value = 0.04326
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1.22327 -0.01913
sample estimates:
mean of x mean of y 
    2.023     2.644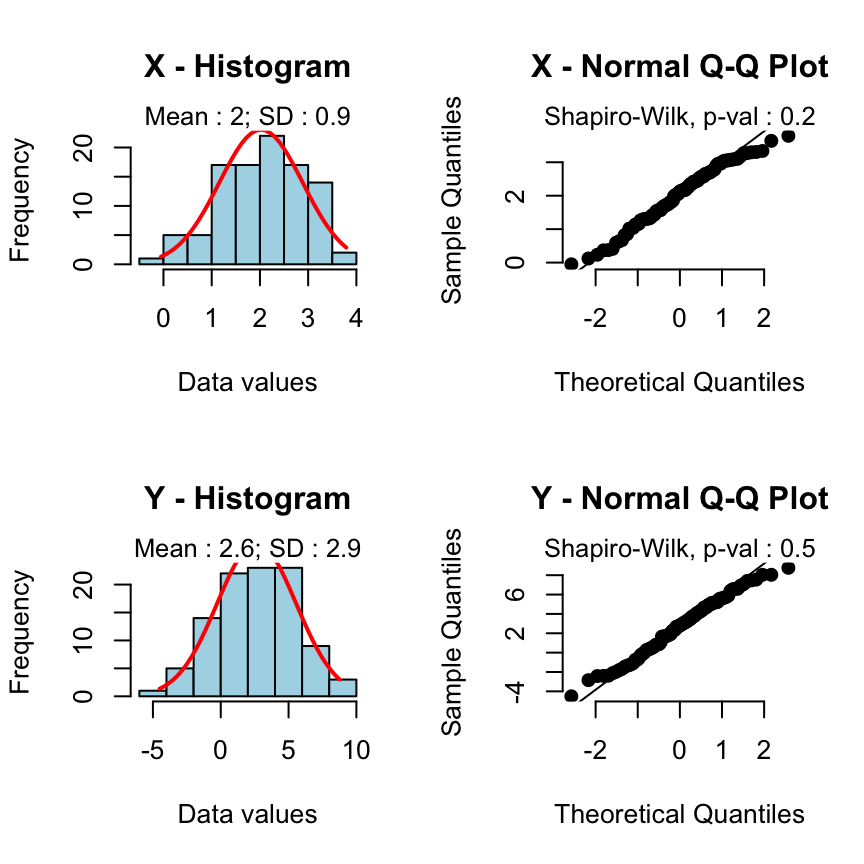 

Le test t de Welch est utilis? automatiquement.

Cas 3 - Les ?chantillons ne sont pas distribu?s selon une loi normale:

source('http://www.sthda.com/upload/rquery_t_test.r')
set.seed(123456789)
x<-rnorm(100, mean=2, sd=0.9)
x<-c(x, 10,20) # add some outliers
y<-rnorm(100, mean=4, sd=1)
rquery.t.test(x, y)

Warning: x or y is not normally distributed : Shapiro test p-value : 2e-17 (for x) and 0.5 (for y).
 Use a non parametric test like Wilcoxon test.

    Welch Two Sample t-test
data:  x and y
t = -8.374, df = 142.2, p-value = 4.809e-14
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -2.395 -1.480
sample estimates:
mean of x mean of y 
    2.277     4.215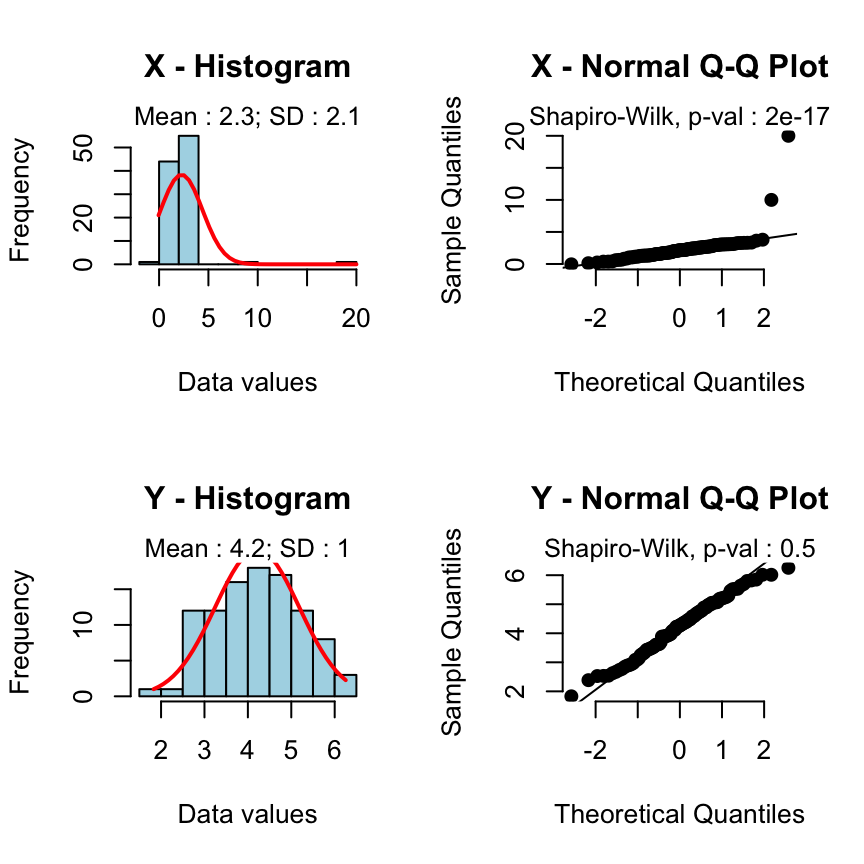 

Un message d?avertissement est affich? et la fonction rquery.t.test vous sugg?re de faire un test non-param?trique de type Wilcoxon.

Test de Student appari? : Compararaison de moyennes de deux s?ries dependantes

source('http://www.sthda.com/upload/rquery_t_test.r')
set.seed(123456789)
x<-rnorm(30, mean=10, sd=2)
y<-rnorm(30, mean=50, sd=3)
rquery.t.test(x, y, paired=TRUE)

    Paired t-test
data:  x and y
t = -56.5, df = 29, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -41.63 -38.72
sample estimates:
mean of the differences 
                 -40.17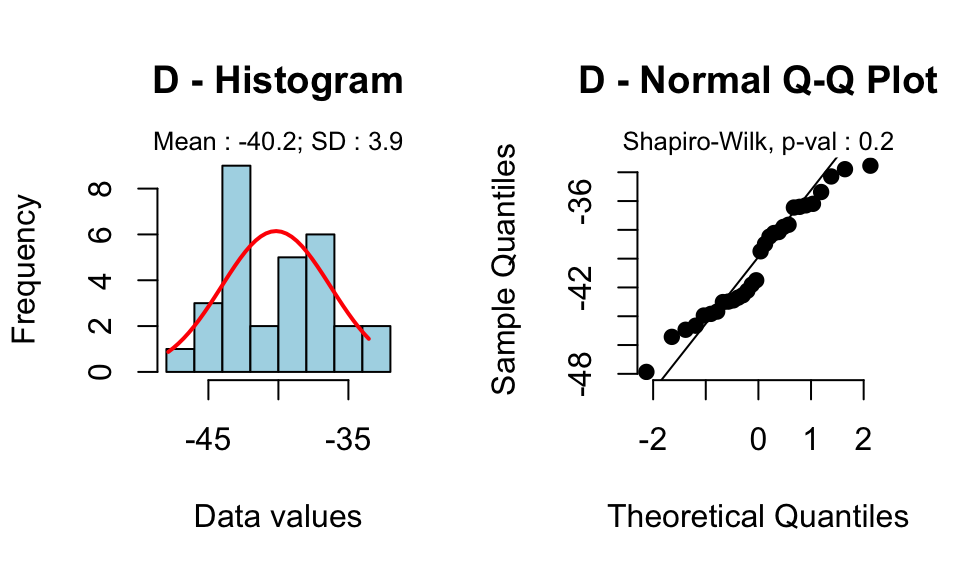 

Lire plus sur test de student appari?

Test de Student en ligne

Code R de la fonction rquery.t.test

#++++++++++++++++++++++++
# rquery.t.test
#+++++++++++++++++++++++
# Description : Performs one or two samples t-test
# x : a (non-empty) numeric vector of data values.
# y : an optional (non-empty) numeric vector of data values
# paired : if TRUE, paired t-test is performed
# graph : if TRUE, the distribution of the data is shown
  # for the inspection of normality
# ... : further arguments to be passed to the built-in t.test() R function
# 1. shapiro.test is used to check normality
# 2. F-test is performed to check equality of variances
# If the variances are different, then Welch t-test is used
rquery.t.test<-function(x, y = NULL, paired = FALSE, 
                        graph = TRUE, ...)
{
  # I. Preliminary test : normality and variance tests
  # ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
  var.equal = FALSE # by default
  
  # I.1 One sample t test
  if(is.null(y)){
    if(graph) par(mfrow=c(1,2))
    shapiro.px<-normaTest(x, graph, 
                          hist.title="X - Histogram",
                          qq.title="X - Normal Q-Q Plot")
    if(shapiro.px < 0.05)
      warning("x is not normally distributed :",
        " Shapiro-Wilk test p-value : ", shapiro.px, 
        ".\n Use a non-parametric test like Wilcoxon test.")
  }
  
  # I.2 Two samples t test
  if(!is.null(y)){
    
      # I.2.a unpaired t test
      if(!paired){
          if(graph) par(mfrow=c(2,2))
          # normality test
          shapiro.px<-normaTest(x, graph, 
                                hist.title="X - Histogram",
                                qq.title="X - Normal Q-Q Plot")
          shapiro.py<-normaTest(y, graph,
                                hist.title="Y - Histogram",
                                qq.title="Y - Normal Q-Q Plot")
          if(shapiro.px < 0.05 | shapiro.py < 0.05){
              warning("x or y is not normally distributed :",
                " Shapiro test p-value : ", shapiro.px,
                " (for x) and ", shapiro.py, " (for y)",
                ".\n Use a non parametric test like Wilcoxon test.")
            }
          # Check for equality of variances
          if(var.test(x,y)$p.value >= 0.05) var.equal=TRUE
        } 
      
      # I.2.b Paired t-test
      else {
        if(graph) par(mfrow=c(1,2))
        d = x-y 
        shapiro.pd<-normaTest(d, graph, 
                              hist.title="D - Histogram",
                              qq.title="D - Normal Q-Q Plot")
        if(shapiro.pd < 0.05 )
          warning("The difference d ( = x-y) is not normally distributed :",
                " Shapiro-Wilk test p-value : ", shapiro.pd, 
                ".\n Use a non-parametric test like Wilcoxon test.")
      } 
      
   }
  
  # II. Student's t-test
  # ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
  res <- t.test(x, y, paired=paired, var.equal=var.equal, ...)
  return(res)
}
#+++++++++++++++++++++++
# Helper function
#+++++++++++++++++++++++
# Performs normality test using Shapiro Wilk's method
# The histogram and Q-Q plot of the data are plotted
# x : a (non-empty) numeric vector of data values.
# graph : possible values are TRUE or FALSE. If TRUE,
  # the histogram and the Q-Q plot of the data are displayed
# hist.title : title of the histogram
# qq.title : title of the Q-Q plot
normaTest<-function(x, graph=TRUE, 
                    hist.title="Histogram", 
                    qq.title="Normal Q-Q Plot",...)
  {  
  # Significance test
  #++++++++++++++++++++++
  shapiro.p<-signif(shapiro.test(x)$p.value,1) 
  
  if(graph){
    # Plot : Visual inspection
    #++++++++++++++++
    h<-hist(x, col="lightblue", main=hist.title, 
            xlab="Data values", ...)
    m<-round(mean(x),1)
    s<-round(sd(x),1)
    mtext(paste0("Mean : ", m, "; SD : ", s),
          side=3, cex=0.8)
    # add normal curve
    xfit<-seq(min(x),max(x),length=40)
    yfit<-dnorm(xfit,mean=mean(x),sd=sd(x))
    yfit <- yfit*diff(h$mids[1:2])*length(x)
    lines(xfit, yfit, col="red", lwd=2)
    # qq plot
    qqnorm(x, pch=19, frame.plot=FALSE,main=qq.title)
    qqline(x)
    mtext(paste0("Shapiro-Wilk, p-val : ", shapiro.p),
          side=3, cex=0.8)
  }
  return(shapiro.p)
}

Infos

Cette analyse a ?t? effectu? avec R (ver. 3.1.0).

References

1. Asghar Ghasemi, Saleh Zahediasl; Normality Tests for Statistical Analysis: A Guide for Non-Statisticians; Int J Endocrinol Metab. 2012;10(2):486-489.
2. Rochon J1, Gondan M, Kieser M.; To test or not to test: Preliminary assessment of normality when comparing two independent samples; BMC Med Res Methodol. 2012 Jun 19;12:81.