MCA - Multiple Correspondence Analysis in R: Essentials
The Multiple correspondence analysis (MCA) is an extension of the simple correspondence analysis (chapter @ref(correspondence-analysis)) for summarizing and visualizing a data table containing more than two categorical variables. It can also be seen as a generalization of principal component analysis when the variables to be analyzed are categorical instead of quantitative (Abdi and Williams 2010).
MCA is generally used to analyse a data set from survey. The goal is to identify:
- A group of individuals with similar profile in their answers to the questions
- The associations between variable categories
Previously, we described how to compute and interpret the simple correspondence analysis (chapter @ref(correspondence-analysis)). In the current chapter, we demonstrate how to compute and visualize multiple correspondence analysis in R software using FactoMineR (for the analysis) and factoextra (for data visualization). Additionally, we’ll show how to reveal the most important variables that contribute the most in explaining the variations in the data set. We continue by explaining how to predict the results for supplementary individuals and variables. Finally, we’ll demonstrate how to filter MCA results in order to keep only the most contributing variables.
Contents:
The Book:
Computation
R packages
Several functions from different packages are available in the R software for computing multiple correspondence analysis. These functions/packages include:
- MCA() function [FactoMineR package]
- dudi.mca() function [ade4 package]
- and epMCA() [ExPosition package]
No matter what function you decide to use, you can easily extract and visualize the MCA results using R functions provided in the factoextra R package.
Here, we’ll use FactoMineR (for the analysis) and factoextra (for ggplot2-based elegant visualization). To install the two packages, type this:
install.packages(c("FactoMineR", "factoextra"))Load the packages:
library("FactoMineR")
library("factoextra")Data format
We’ll use the demo data sets poison available in FactoMineR package:
data(poison)
head(poison[, 1:7], 3)## Age Time Sick Sex Nausea Vomiting Abdominals
## 1 9 22 Sick_y F Nausea_y Vomit_n Abdo_y
## 2 5 0 Sick_n F Nausea_n Vomit_n Abdo_n
## 3 6 16 Sick_y F Nausea_n Vomit_y Abdo_yThis data is a result from a survey carried out on children of primary school who suffered from food poisoning. They were asked about their symptoms and about what they ate.
The data contains 55 rows (individuals) and 15 columns (variables). We’ll use only some of these individuals (children) and variables to perform the multiple correspondence analysis. The coordinates of the remaining individuals and variables on the factor map will be predicted from the previous MCA results.
In MCA terminology, our data contains :
- Active individuals (rows 1:55): Individuals that are used in the multiple correspondence analysis.
- Active variables (columns 5:15) : Variables that are used in the MCA.
-
Supplementary variables: They don’t participate to the MCA. The coordinates of these variables will be predicted.
- Supplementary quantitative variables (quanti.sup): Columns 1 and 2 corresponding to the columns age and time, respectively.
- Supplementary qualitative variables (quali.sup: Columns 3 and 4 corresponding to the columns Sick and Sex, respectively. This factor variables will be used to color individuals by groups.
Subset only active individuals and variables for multiple correspondence analysis:
poison.active <- poison[1:55, 5:15]
head(poison.active[, 1:6], 3)## Nausea Vomiting Abdominals Fever Diarrhae Potato
## 1 Nausea_y Vomit_n Abdo_y Fever_y Diarrhea_y Potato_y
## 2 Nausea_n Vomit_n Abdo_n Fever_n Diarrhea_n Potato_y
## 3 Nausea_n Vomit_y Abdo_y Fever_y Diarrhea_y Potato_yData summary
The R base function summary() can be used to compute the frequency of variable categories. As the data table contains a large number of variables, we’ll display only the results for the first 4 variables.
Statistical summaries:
# Summary of the 4 first variables
summary(poison.active)[, 1:4]## Nausea Vomiting Abdominals Fever
## Nausea_n:43 Vomit_n:33 Abdo_n:18 Fever_n:20
## Nausea_y:12 Vomit_y:22 Abdo_y:37 Fever_y:35The summary() functions return the size of each variable category.
It’s also possible to plot the frequency of variable categories. The R code below, plots the first 4 columns:
for (i in 1:4) {
plot(poison.active[,i], main=colnames(poison.active)[i],
ylab = "Count", col="steelblue", las = 2)
}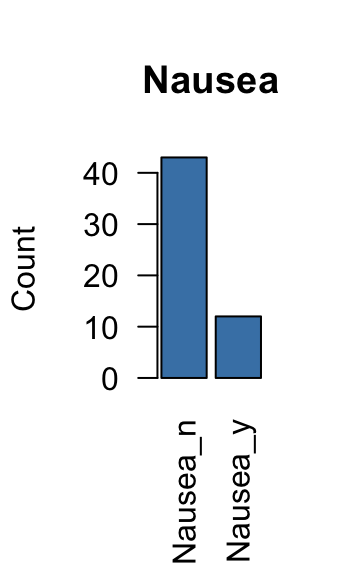
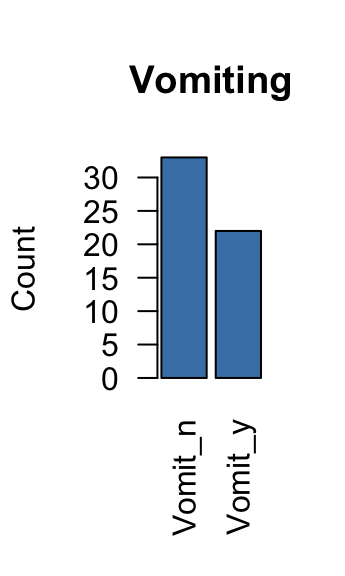
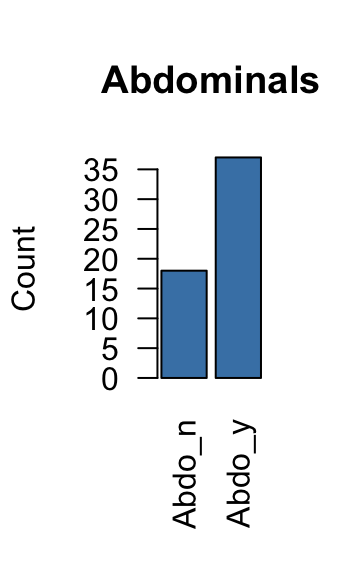
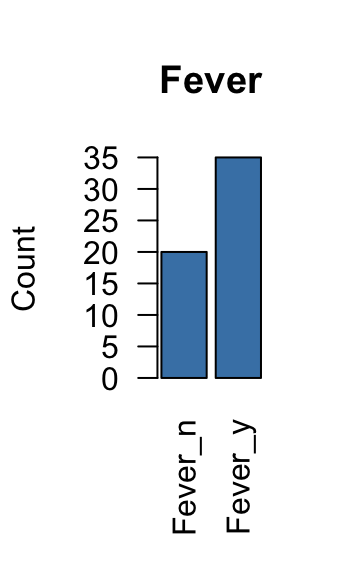
The graphs above can be used to identify variable categories with a very low frequency. These types of variables can distort the analysis and should be removed.
R code
The function MCA()[FactoMiner package] can be used. A simplified format is :
MCA(X, ncp = 5, graph = TRUE)X: a data frame with n rows (individuals) and p columns (categorical variables)ncp: number of dimensions kept in the final results.graph: a logical value. If TRUE a graph is displayed.
In the R code below, the MCA is performed only on the active individuals/variables :
res.mca <- MCA(poison.active, graph = FALSE)The output of the MCA() function is a list including :
print(res.mca)## **Results of the Multiple Correspondence Analysis (MCA)**
## The analysis was performed on 55 individuals, described by 11 variables
## *The results are available in the following objects:
##
## name description
## 1 "$eig" "eigenvalues"
## 2 "$var" "results for the variables"
## 3 "$var$coord" "coord. of the categories"
## 4 "$var$cos2" "cos2 for the categories"
## 5 "$var$contrib" "contributions of the categories"
## 6 "$var$v.test" "v-test for the categories"
## 7 "$ind" "results for the individuals"
## 8 "$ind$coord" "coord. for the individuals"
## 9 "$ind$cos2" "cos2 for the individuals"
## 10 "$ind$contrib" "contributions of the individuals"
## 11 "$call" "intermediate results"
## 12 "$call$marge.col" "weights of columns"
## 13 "$call$marge.li" "weights of rows"The object that is created using the function MCA() contains many information found in many different lists and matrices. These values are described in the next section.
Visualization and interpretation
We’ll use the factoextra R package to help in the interpretation and the visualization of the multiple correspondence analysis. No matter what function you decide to use [FactoMiner::MCA(), ade4::dudi.mca()], you can easily extract and visualize the results of multiple correspondence analysis using R functions provided in the factoextra R package.
These factoextra functions include:
get_eigenvalue(res.mca): Extract the eigenvalues/variances retained by each dimension (axis)fviz_eig(res.mca): Visualize the eigenvalues/variancesget_mca_ind(res.mca),get_mca_var(res.mca): Extract the results for individuals and variables, respectively.fviz_mca_ind(res.mca),fviz_mca_var(res.mca): Visualize the results for individuals and variables, respectively.fviz_mca_biplot(res.mca): Make a biplot of rows and columns.
In the next sections, we’ll illustrate each of these functions.
Eigenvalues / Variances
The proportion of variances retained by the different dimensions (axes) can be extracted using the function get_eigenvalue() [factoextra package] as follow:
library("factoextra")
eig.val <- get_eigenvalue(res.mca)
# head(eig.val)To visualize the percentages of inertia explained by each MCA dimensions, use the function fviz_eig() or fviz_screeplot() [factoextra package]:
fviz_screeplot(res.mca, addlabels = TRUE, ylim = c(0, 45))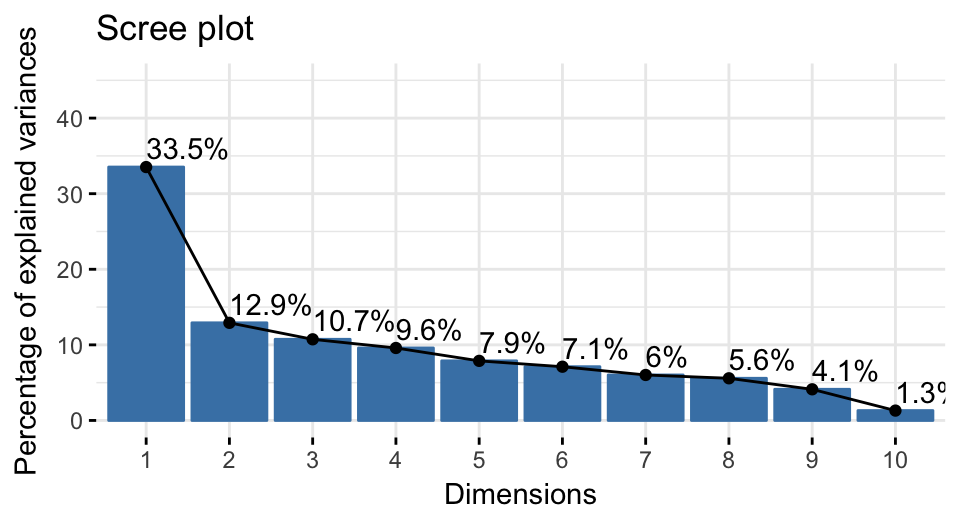
Biplot
The function fviz_mca_biplot() [factoextra package] is used to draw the biplot of individuals and variable categories:
fviz_mca_biplot(res.mca,
repel = TRUE, # Avoid text overlapping (slow if many point)
ggtheme = theme_minimal())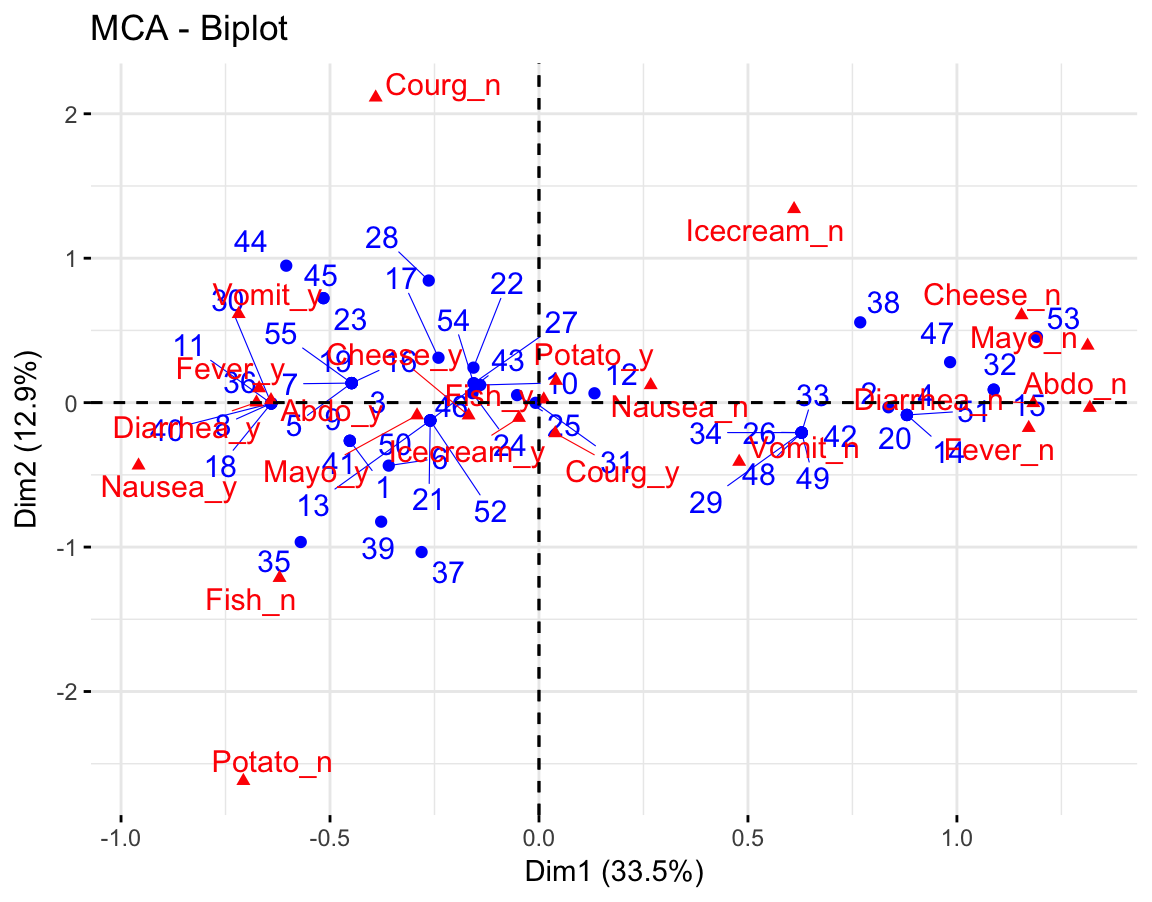
The plot above shows a global pattern within the data. Rows (individuals) are represented by blue points and columns (variable categories) by red triangles.
The distance between any row points or column points gives a measure of their similarity (or dissimilarity). Row points with similar profile are closed on the factor map. The same holds true for column points.
Graph of variables
Results
The function get_mca_var() [in factoextra] is used to extract the results for variable categories. This function returns a list containing the coordinates, the cos2 and the contribution of variable categories:
var <- get_mca_var(res.mca)
var## Multiple Correspondence Analysis Results for variables
## ===================================================
## Name Description
## 1 "$coord" "Coordinates for categories"
## 2 "$cos2" "Cos2 for categories"
## 3 "$contrib" "contributions of categories"The components of the get_mca_var() can be used in the plot of rows as follow:
var$coord: coordinates of variables to create a scatter plotvar$cos2: represents the quality of the representation for variables on the factor map.var$contrib: contains the contributions (in percentage) of the variables to the definition of the dimensions.
Note that, it’s possible to plot variable categories and to color them according to either i) their quality on the factor map (cos2) or ii) their contribution values to the definition of dimensions (contrib).
The different components can be accessed as follow:
# Coordinates
head(var$coord)
# Cos2: quality on the factore map
head(var$cos2)
# Contributions to the principal components
head(var$contrib)In this section, we’ll describe how to visualize variable categories only. Next, we’ll highlight variable categories according to either i) their quality of representation on the factor map or ii) their contributions to the dimensions.
Correlation between variables and principal dimensions
To visualize the correlation between variables and MCA principal dimensions, type this:
fviz_mca_var(res.mca, choice = "mca.cor",
repel = TRUE, # Avoid text overlapping (slow)
ggtheme = theme_minimal())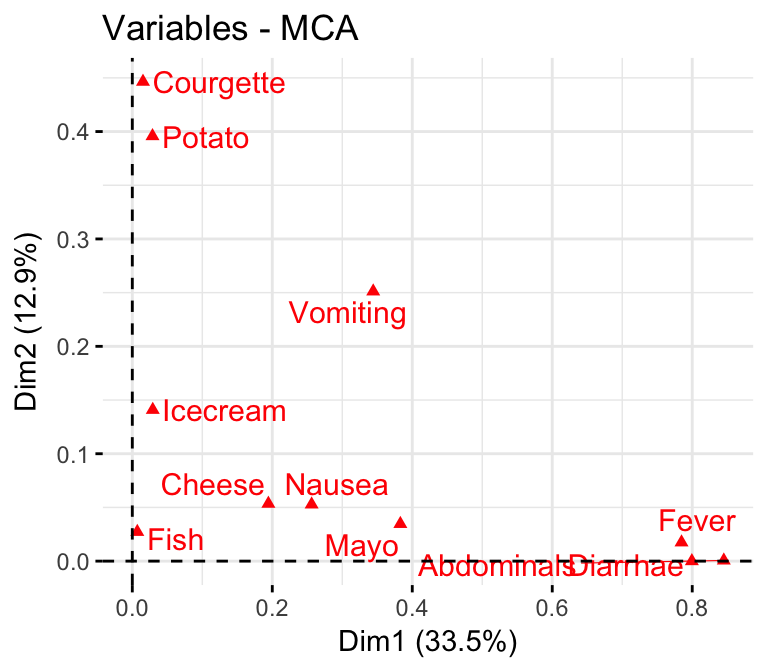
-
The plot above helps to identify variables that are the most correlated with each dimension. The squared correlations between variables and the dimensions are used as coordinates.
-
It can be seen that, the variables Diarrhae, Abdominals and Fever are the most correlated with dimension 1. Similarly, the variables Courgette and Potato are the most correlated with dimension 2.
Coordinates of variable categories
The R code below displays the coordinates of each variable categories in each dimension (1, 2 and 3):
head(round(var$coord, 2), 4)## Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
## Nausea_n 0.27 0.12 -0.27 0.03 0.07
## Nausea_y -0.96 -0.43 0.95 -0.12 -0.26
## Vomit_n 0.48 -0.41 0.08 0.27 0.05
## Vomit_y -0.72 0.61 -0.13 -0.41 -0.08Use the function fviz_mca_var() [in factoextra] to visualize only variable categories:
fviz_mca_var(res.mca,
repel = TRUE, # Avoid text overlapping (slow)
ggtheme = theme_minimal())
It’s possible to change the color and the shape of the variable points using the arguments col.var and shape.var as follow:
fviz_mca_var(res.mca, col.var="black", shape.var = 15,
repel = TRUE)The plot above shows the relationships between variable categories. It can be interpreted as follow:
- Variable categories with a similar profile are grouped together.
- Negatively correlated variable categories are positioned on opposite sides of the plot origin (opposed quadrants).
- The distance between category points and the origin measures the quality of the variable category on the factor map. Category points that are away from the origin are well represented on the factor map.
Quality of representation of variable categories
The two dimensions 1 and 2 are sufficient to retain 46% of the total inertia (variation) contained in the data. Not all the points are equally well displayed in the two dimensions.
The quality of the representation is called the squared cosine (cos2), which measures the degree of association between variable categories and a particular axis. The cos2 of variable categories can be extracted as follow:
head(var$cos2, 4)## Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
## Nausea_n 0.256 0.0528 0.2527 0.00408 0.01947
## Nausea_y 0.256 0.0528 0.2527 0.00408 0.01947
## Vomit_n 0.344 0.2512 0.0107 0.11229 0.00413
## Vomit_y 0.344 0.2512 0.0107 0.11229 0.00413If a variable category is well represented by two dimensions, the sum of the cos2 is closed to one. For some of the row items, more than 2 dimensions are required to perfectly represent the data.
It’s possible to color variable categories by their cos2 values using the argument col.var = “cos2”. This produces a gradient colors, which can be customized using the argument gradient.cols. For instance, gradient.cols = c("white", "blue", "red") means that:
- variable categories with low cos2 values will be colored in “white”
- variable categories with mid cos2 values will be colored in “blue”
- variable categories with high cos2 values will be colored in “red”
# Color by cos2 values: quality on the factor map
fviz_mca_var(res.mca, col.var = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE, # Avoid text overlapping
ggtheme = theme_minimal())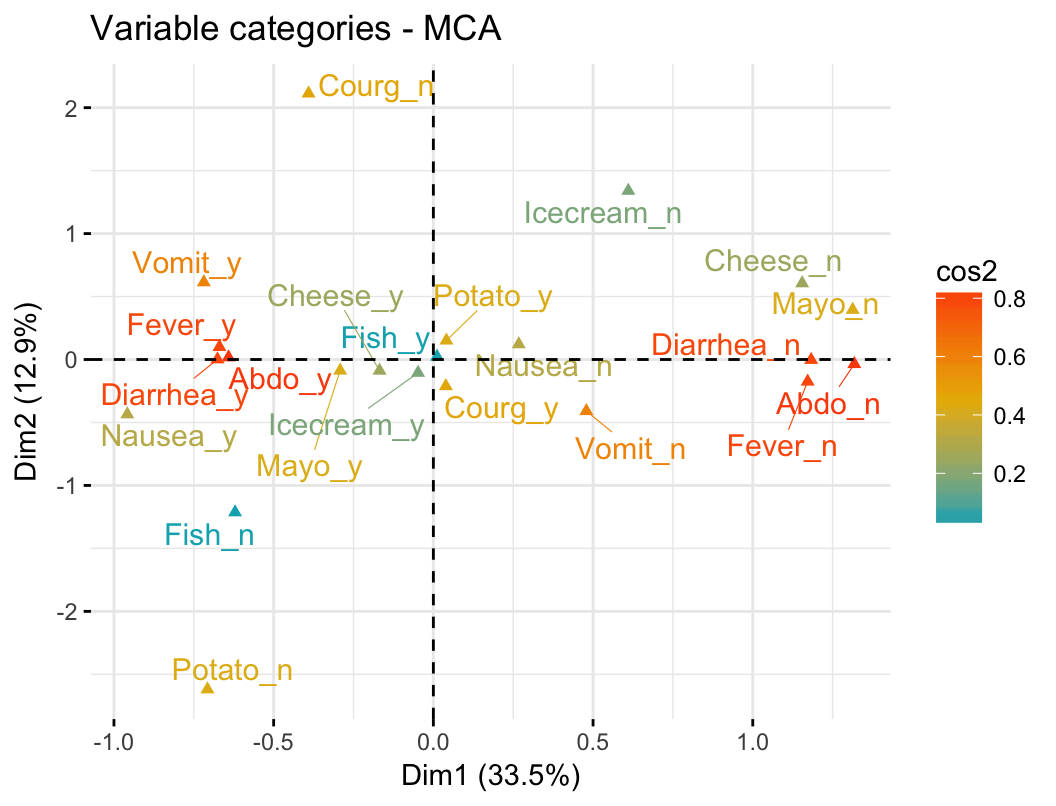
Note that, it’s also possible to change the transparency of the variable categories according to their cos2 values using the option alpha.var = "cos2". For example, type this:
# Change the transparency by cos2 values
fviz_mca_var(res.mca, alpha.var="cos2",
repel = TRUE,
ggtheme = theme_minimal())You can visualize the cos2 of row categories on all the dimensions using the corrplot package:
library("corrplot")
corrplot(var$cos2, is.corr=FALSE)It’s also possible to create a bar plot of variable cos2 using the function fviz_cos2()[in factoextra]:
# Cos2 of variable categories on Dim.1 and Dim.2
fviz_cos2(res.mca, choice = "var", axes = 1:2)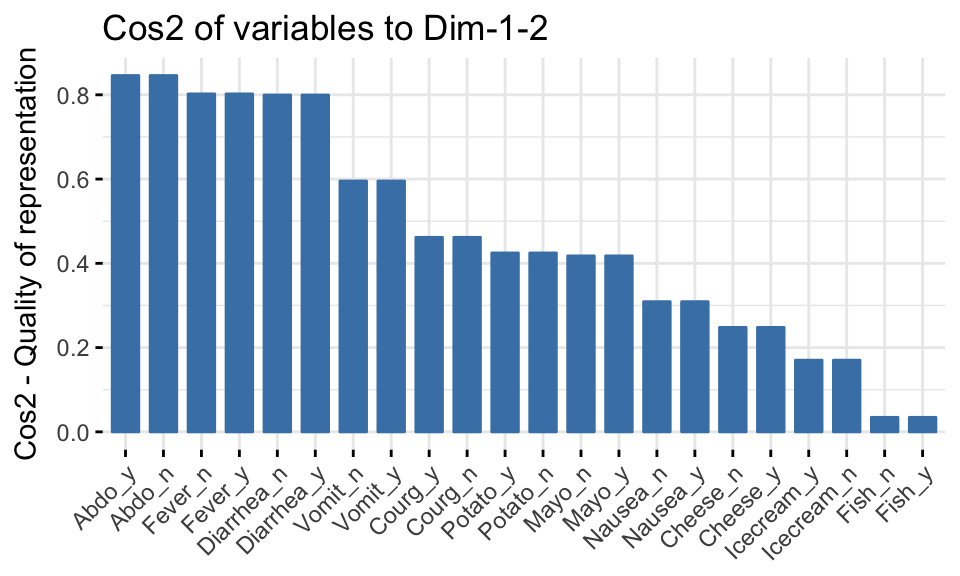
Note that, variable categories Fish_n, Fish_y, Icecream_n and Icecream_y are not very well represented by the first two dimensions. This implies that the position of the corresponding points on the scatter plot should be interpreted with some caution. A higher dimensional solution is probably necessary.
Contribution of variable categories to the dimensions
The contribution of the variable categories (in %) to the definition of the dimensions can be extracted as follow:
head(round(var$contrib,2), 4)## Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
## Nausea_n 1.52 0.81 4.67 0.08 0.49
## Nausea_y 5.43 2.91 16.73 0.30 1.76
## Vomit_n 3.73 7.07 0.36 4.26 0.19
## Vomit_y 5.60 10.61 0.54 6.39 0.29The variable categories with the larger value, contribute the most to the definition of the dimensions. Variable categories that contribute the most to Dim.1 and Dim.2 are the most important in explaining the variability in the data set.
The function fviz_contrib() [factoextra package] can be used to draw a bar plot of the contribution of variable categories. The R code below shows the top 15 variable categories contributing to the dimensions:
# Contributions of rows to dimension 1
fviz_contrib(res.mca, choice = "var", axes = 1, top = 15)
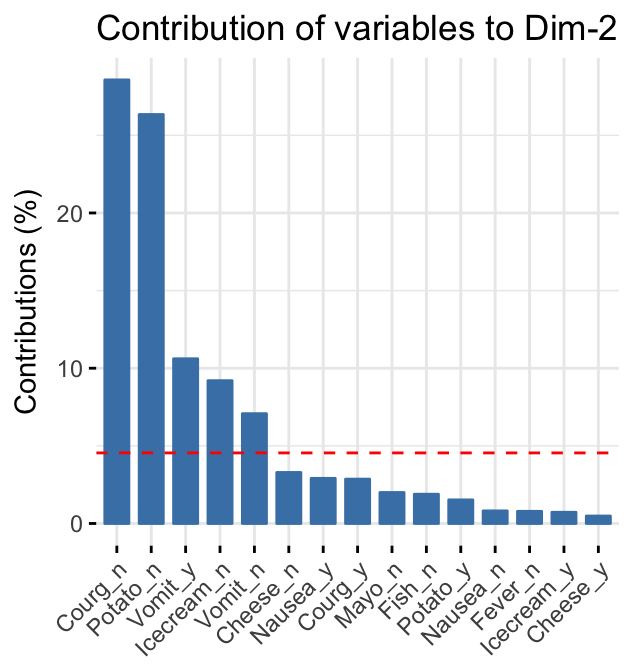
# Contributions of rows to dimension 2
fviz_contrib(res.mca, choice = "var", axes = 2, top = 15)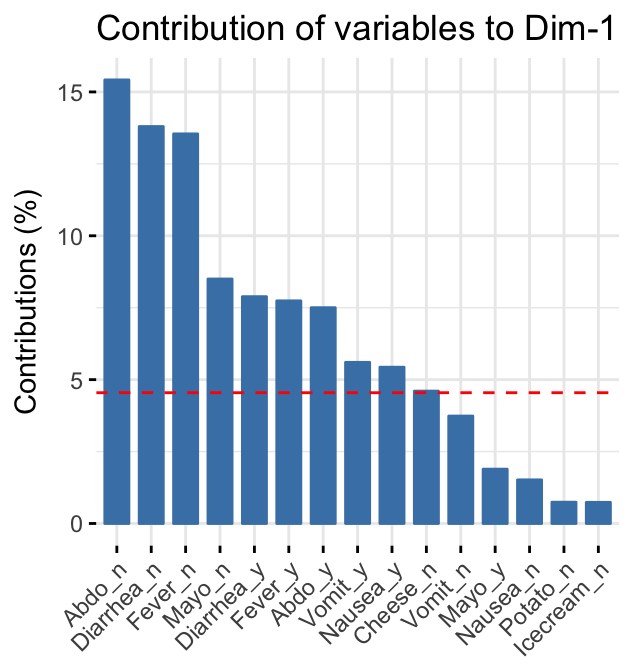
The total contributions to dimension 1 and 2 are obtained as follow:
# Total contribution to dimension 1 and 2
fviz_contrib(res.mca, choice = "var", axes = 1:2, top = 15)The red dashed line on the graph above indicates the expected average value, If the contributions were uniform. The calculation of the expected contribution value, under null hypothesis, has been detailed in the principal component analysis chapter.
It can be seen that:
- the categories Abdo_n, Diarrhea_n, Fever_n and Mayo_n are the most important in the definition of the first dimension.
- The categories Courg_n, Potato_n, Vomit_y and Icecream_n contribute the most to the dimension 2
The most important (or, contributing) variable categories can be highlighted on the scatter plot as follow:
fviz_mca_var(res.mca, col.var = "contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE, # avoid text overlapping (slow)
ggtheme = theme_minimal()
)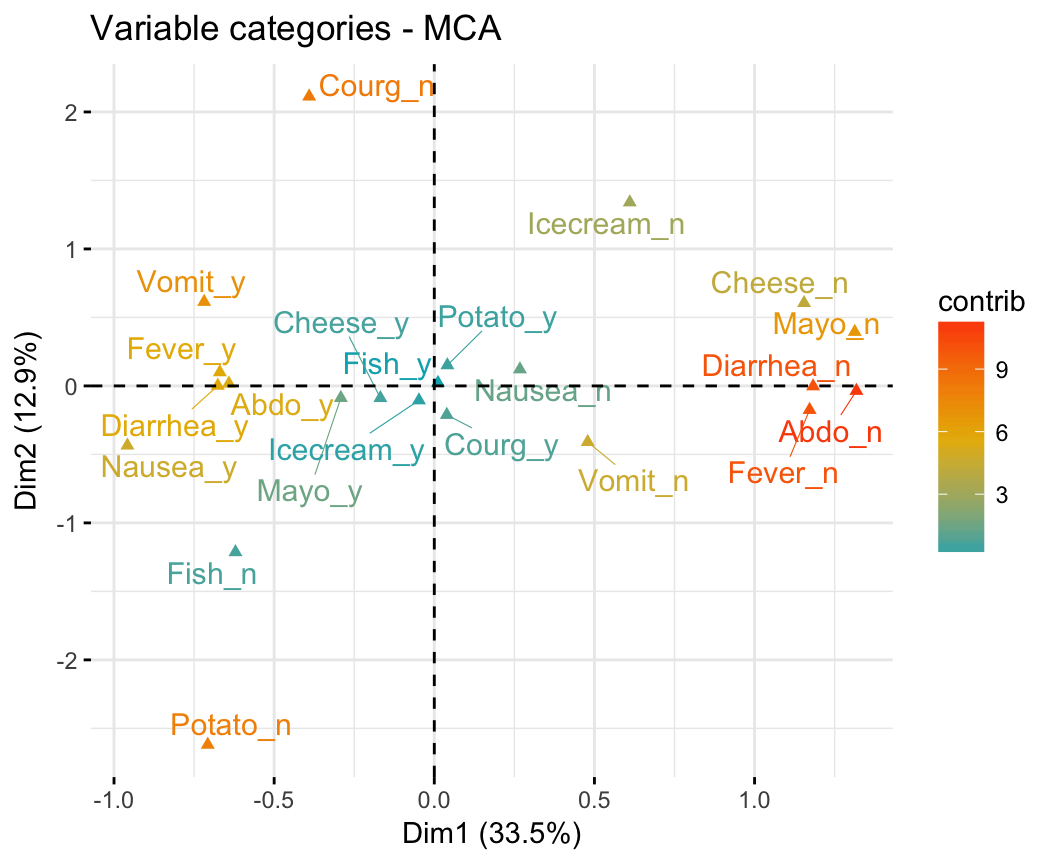
The plot above gives an idea of what pole of the dimensions the categories are actually contributing to.
It is evident that the categories Abdo_n, Diarrhea_n, Fever_n and Mayo_n have an important contribution to the positive pole of the first dimension, while the categories Fever_y and Diarrhea_y have a major contribution to the negative pole of the first dimension; etc, ….
Note that, it’s also possible to control the transparency of variable categories according to their contribution values using the option alpha.var = "contrib". For example, type this:
# Change the transparency by contrib values
fviz_mca_var(res.mca, alpha.var="contrib",
repel = TRUE,
ggtheme = theme_minimal())Graph of individuals
Results
The function get_mca_ind() [in factoextra] is used to extract the results for individuals. This function returns a list containing the coordinates, the cos2 and the contributions of individuals:
ind <- get_mca_ind(res.mca)
ind## Multiple Correspondence Analysis Results for individuals
## ===================================================
## Name Description
## 1 "$coord" "Coordinates for the individuals"
## 2 "$cos2" "Cos2 for the individuals"
## 3 "$contrib" "contributions of the individuals"The result for individuals gives the same information as described for variable categories. For this reason, I’ll just displayed the result for individuals in this section without commenting.
To get access to the different components, use this:
# Coordinates of column points
head(ind$coord)
# Quality of representation
head(ind$cos2)
# Contributions
head(ind$contrib)Plots: quality and contribution
The function fviz_mca_ind() [in factoextra] is used to visualize only individuals. Like variable categories, it’s also possible to color individuals by their cos2 values:
fviz_mca_ind(res.mca, col.ind = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE, # Avoid text overlapping (slow if many points)
ggtheme = theme_minimal())
The R code below creates a bar plots of individuals cos2 and contributions:
# Cos2 of individuals
fviz_cos2(res.mca, choice = "ind", axes = 1:2, top = 20)
# Contribution of individuals to the dimensions
fviz_contrib(res.mca, choice = "ind", axes = 1:2, top = 20)Color individuals by groups
Note that, it’s possible to color the individuals using any of the qualitative variables in the initial data table (poison)
The R code below colors the individuals by groups using the levels of the variable Vomiting. The argument habillage is used to specify the factor variable for coloring the individuals by groups. A concentration ellipse can be also added around each group using the argument addEllipses = TRUE. If you want a confidence ellipse around the mean point of categories, use ellipse.type = "confidence" The argument palette is used to change group colors.
fviz_mca_ind(res.mca,
label = "none", # hide individual labels
habillage = "Vomiting", # color by groups
palette = c("#00AFBB", "#E7B800"),
addEllipses = TRUE, ellipse.type = "confidence",
ggtheme = theme_minimal()) 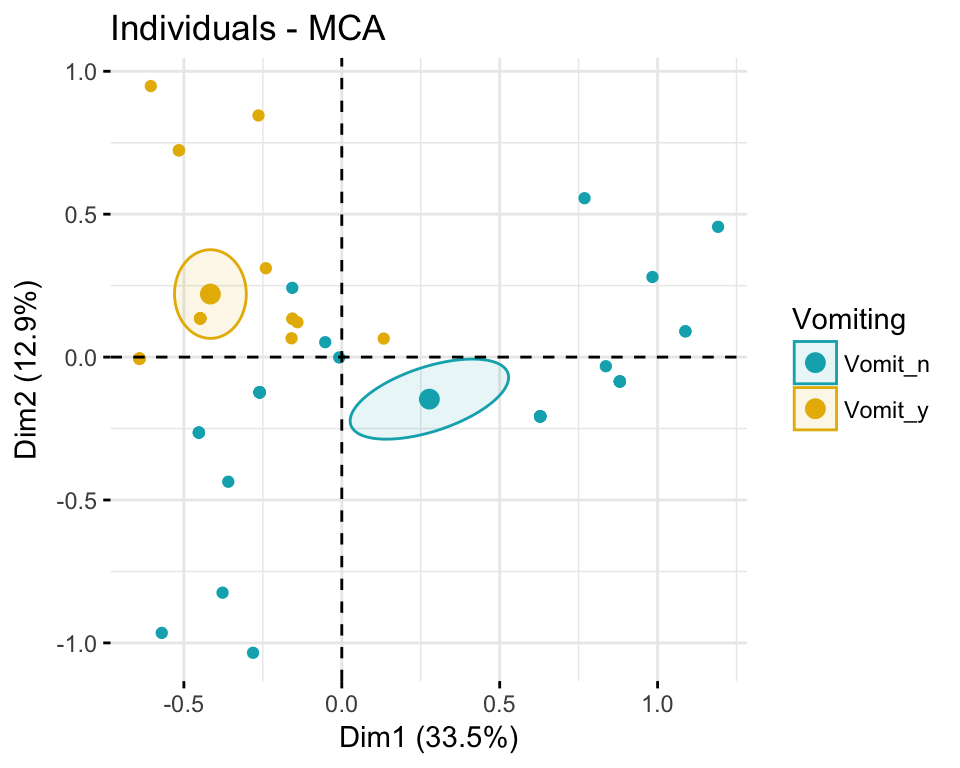
Note that, to specify the value of the argument habillage, it’s also possible to use the index of the column as follow (habillage = 2). Additionally, you can provide an external grouping variable as follow: habillage = poison$Vomiting. For example:
# habillage = index of the column to be used as grouping variable
fviz_mca_ind(res.mca, habillage = 2, addEllipses = TRUE)
# habillage = external grouping variable
fviz_mca_ind(res.mca, habillage = poison$Vomiting, addEllipses = TRUE)If you want to color individuals using multiple categorical variables at the same time, use the function fviz_ellipses() [in factoextra] as follow:
fviz_ellipses(res.mca, c("Vomiting", "Fever"),
geom = "point")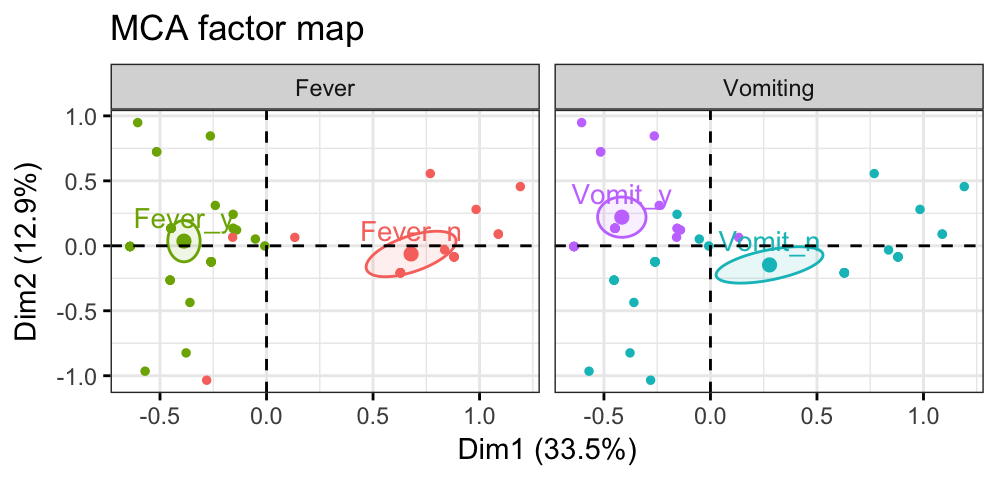
Alternatively, you can specify categorical variable indices:
fviz_ellipses(res.mca, 1:4, geom = "point")Dimension description
The function dimdesc() [in FactoMineR] can be used to identify the most correlated variables with a given dimension:
res.desc <- dimdesc(res.mca, axes = c(1,2))
# Description of dimension 1
res.desc[[1]]
# Description of dimension 2
res.desc[[2]]Supplementary elements
Definition and types
As described above (section @ref(mca-data-format)), the data set poison contains:
- supplementary continuous variables (quanti.sup = 1:2, columns 1 and 2 corresponding to the columns
ageandtime, respectively) - supplementary qualitative variables (quali.sup = 3:4, corresponding to the columns
SickandSex, respectively). This factor variables are used to color individuals by groups
The data doesn’t contain supplementary individuals. However, for demonstration, we’ll use the individuals 53:55 as supplementary individuals.
Supplementary variables and individuals are not used for the determination of the principal dimensions. Their coordinates are predicted using only the information provided by the performed multiple correspondence analysis on active variables/individuals.
Specification in MCA
To specify supplementary individuals and variables, the function MCA() can be used as follow :
MCA(X, ind.sup = NULL, quanti.sup = NULL, quali.sup=NULL,
graph = TRUE, axes = c(1,2))X: a data frame. Rows are individuals and columns are variables.ind.sup: a numeric vector specifying the indexes of the supplementary individuals.quanti.sup,quali.sup: a numeric vector specifying, respectively, the indexes of the quantitative and qualitative variables.graph: a logical value. If TRUE a graph is displayed.axes: a vector of length 2 specifying the components to be plotted.
For example, type this:
res.mca <- MCA(poison, ind.sup = 53:55,
quanti.sup = 1:2, quali.sup = 3:4, graph=FALSE)Results
The predicted results for supplementary individuals/variables can be extracted as follow:
# Supplementary qualitative variable categories
res.mca$quali.sup
# Supplementary quantitative variables
res.mca$quanti
# Supplementary individuals
res.mca$ind.supPlots
To make a biplot of individuals and variable categories, type this:
# Biplot of individuals and variable categories
fviz_mca_biplot(res.mca, repel = TRUE,
ggtheme = theme_minimal())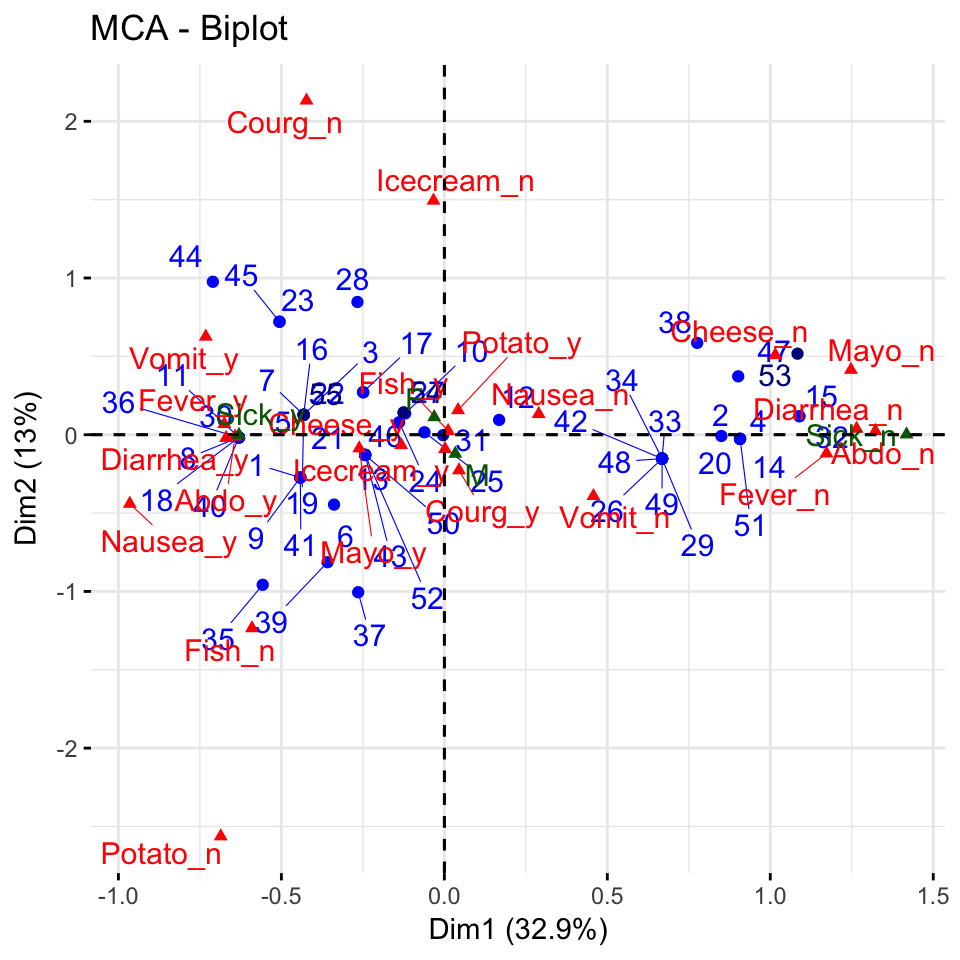
- Active individuals are in blue
- Supplementary individuals are in darkblue
- Active variable categories are in red
- Supplementary variable categories are in darkgreen
If you want to highlight the correlation between variables (active & supplementary) and dimensions, use the function fviz_mca_var() with the argument choice = “mca.cor”:
fviz_mca_var(res.mca, choice = "mca.cor",
repel = TRUE)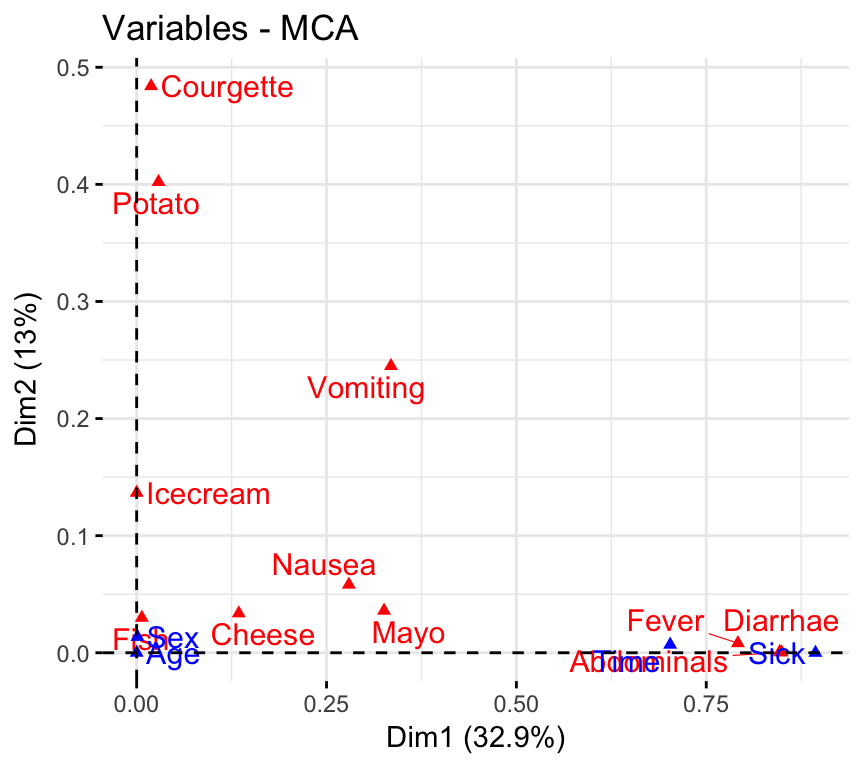
The R code below plots qualitative variable categories (active & supplementary variables):
fviz_mca_var(res.mca, repel = TRUE,
ggtheme= theme_minimal())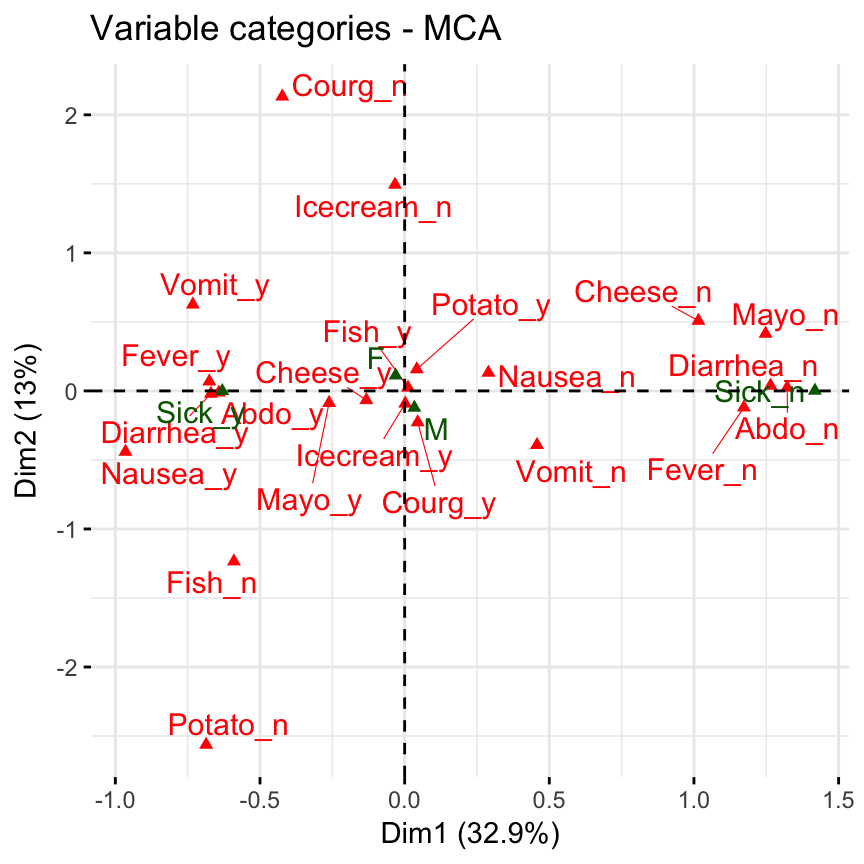
For supplementary quantitative variables, type this:
fviz_mca_var(res.mca, choice = "quanti.sup",
ggtheme = theme_minimal())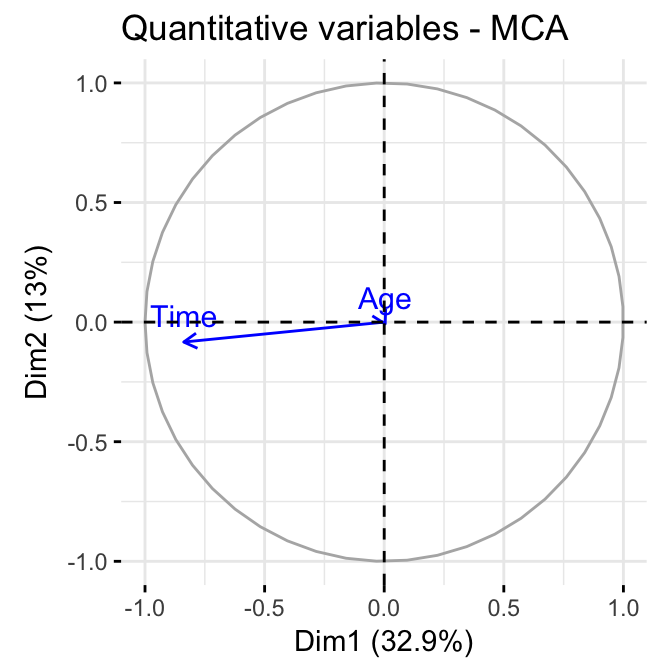
To visualize supplementary individuals, type this:
fviz_mca_ind(res.mca,
label = "ind.sup", #Show the label of ind.sup only
ggtheme = theme_minimal())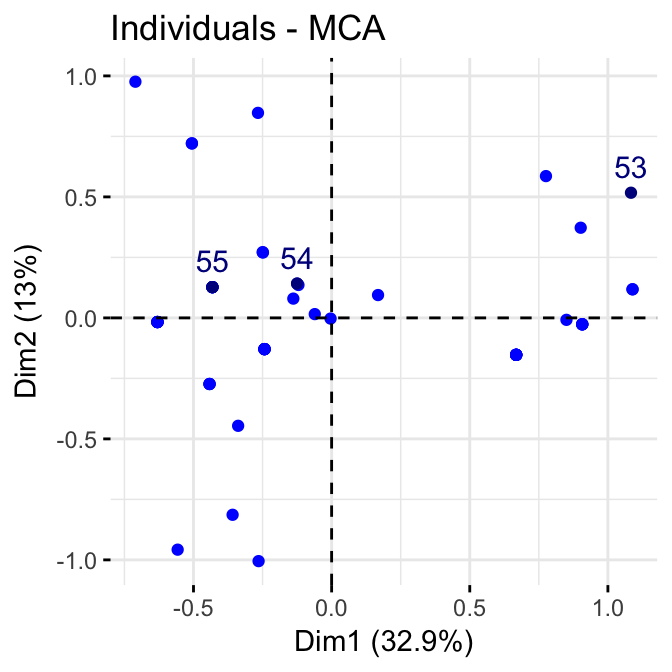
Filtering results
If you have many individuals/variable categories, it’s possible to visualize only some of them using the arguments select.ind and select.var.
select.ind, select.var: a selection of individuals/variable categories to be drawn. Allowed values are NULL or a list containing the arguments name, cos2 or contrib:
name: is a character vector containing individuals/variable category names to be plottedcos2: if cos2 is in [0, 1], ex: 0.6, then individuals/variable categories with a cos2 > 0.6 are plottedif cos2 > 1, ex: 5, then the top 5 active individuals/variable categories and top 5 supplementary columns/rows with the highest cos2 are plottedcontrib: if contrib > 1, ex: 5, then the top 5 individuals/variable categories with the highest contributions are plotted
# Visualize variable categories with cos2 >= 0.4
fviz_mca_var(res.mca, select.var = list(cos2 = 0.4))
# Top 10 active variables with the highest cos2
fviz_mca_var(res.mca, select.var= list(cos2 = 10))
# Select by names
name <- list(name = c("Fever_n", "Abdo_y", "Diarrhea_n",
"Fever_Y", "Vomit_y", "Vomit_n"))
fviz_mca_var(res.mca, select.var = name)
# top 5 contributing individuals and variable categories
fviz_mca_biplot(res.mca, select.ind = list(contrib = 5),
select.var = list(contrib = 5),
ggtheme = theme_minimal())When the selection is done according to the contribution values, supplementary individuals/variable categories are not shown because they don’t contribute to the construction of the axes.
Exporting results
Export plots to PDF/PNG files
Two steps:
- Create the plot of interest as an R object:
# Scree plot
scree.plot <- fviz_eig(res.mca)
# Biplot of row and column variables
biplot.mca <- fviz_mca_biplot(res.mca)- Export the plots into a single pdf file as follow (one plot per page):
library(ggpubr)
ggexport(plotlist = list(scree.plot, biplot.mca),
filename = "MCA.pdf")More options at: Chapter @ref(principal-component-analysis) (section: Exporting results).
Export results to txt/csv files
Easy to use R function: write.infile() [in FactoMineR] package.
# Export into a TXT file
write.infile(res.mca, "mca.txt", sep = "\t")
# Export into a CSV file
write.infile(res.mca, "mca.csv", sep = ";")Summary
In conclusion, we described how to perform and interpret multiple correspondence analysis (CA). We computed MCA using the MCA() function [FactoMineR package]. Next, we used the factoextra R package to produce ggplot2-based visualization of the CA results.
Other functions [packages] to compute MCA in R, include:
- Using
dudi.acm()[ade4]
library("ade4")
res.mca <- dudi.acm(poison.active, scannf = FALSE, nf = 5)- Using
epMCA()[ExPosition]
library("ExPosition")
res.mca <- epMCA(poison.active, graph = FALSE, correction = "bg")No matter what functions you decide to use, in the list above, the factoextra package can handle the output.
fviz_eig(res.mca) # Scree plot
fviz_mca_biplot(res.mca) # Biplot of rows and columnsFurther reading
For the mathematical background behind MCA, refer to the following video courses, articles and books:
- Correspondence Analysis Course Using FactoMineR (Video courses). https://goo.gl/Hhh6hC
- Exploratory Multivariate Analysis by Example Using R (book) (Husson, Le, and Pagès 2017).
- Principal component analysis (article) (Abdi and Williams 2010). https://goo.gl/1Vtwq1.
- Correspondence analysis basics (blog post). https://goo.gl/Xyk8KT.
References
Abdi, Hervé, and Lynne J. Williams. 2010. “Principal Component Analysis.” John Wiley and Sons, Inc. WIREs Comp Stat 2: 433–59. http://staff.ustc.edu.cn/~zwp/teach/MVA/abdi-awPCA2010.pdf.
Husson, Francois, Sebastien Le, and Jérôme Pagès. 2017. Exploratory Multivariate Analysis by Example Using R. 2nd ed. Boca Raton, Florida: Chapman; Hall/CRC. http://factominer.free.fr/bookV2/index.html.



