Unsupervised Learning Essentials
Unsupervised learning refers to a set of statistical techniques for exploring and discovering knowledge, from a multivariate data, without building a predictive models.
It makes it possible to visualize the relationship between variables, as well as, to identify groups of similar individuals (or observations).
The most popular unsupervised learning methods, include:
- Principal component methods, which consist of summarizing and visualizing the most important information contained in a multivariate data set.
- Cluster analysis for identifying groups of observations with similar profile according to a specific criteria. These techniques include hierarchical clustering and k-means clustering.
Previously, we have published two books entitled “Practical Guide To Cluster Analysis in R” and “Practical Guide To Principal Component Methods”. So, this chapter provides just an overview of unsupervised learning techniques and practical examples in R for visualizing multivariate data sets.
Contents:
Principal component methods
Principal component methods allows us to summarize and visualize the most important information contained in a multivariate data set.
The type of principal component methods to use depends on variable types contained in the data set. This practical guide will describe the following methods:
Principal Component Analysis (PCA), which is one of the most popular multivariate analysis method. The goal of PCA is to summarize the information contained in a continuous (i.e, quantitative) multivariate data by reducing the dimensionality of the data without loosing important information.
Correspondence Analysis (CA), which is an extension of the principal component analysis for analyzing a large contingency table formed by two qualitative variables (or categorical data).
Multiple Correspondence Analysis (MCA), which is an adaptation of CA to a data table containing more than two categorical variables.
Loading required R packages
FactoMineRfor computing principal component methodsfactoextrafor visualizing the output of FactoMineR
library(FactoMineR)
library(factoextra)Principal component analysis
PCA reduces the data into few new dimensions (or axes), which are a linear combination of the original variables. You can visualize a multivariate data by drawing a scatter plot of the first two dimensions, which contain the most important information in the data. Read more at: https://goo.gl/kabVHq.
- Demo data set:
USArrests - Compute PCA using the R function
PCA()[FactoMineR] - Visualize the output using the
factoextraR package (an extension to ggplot2)
- Compute PCA using the demo data set
USArrests. The data set contains statistics, in arrests per 100,000 residents for assault, murder, and rape in each of the 50 US states in 1973.
data("USArrests")
res.pca <- PCA(USArrests, graph = FALSE)- Visualize eigenvalues (or scree plot), that is the percentage of variation (or information), in the data, explained by each principal component.
fviz_eig(res.pca)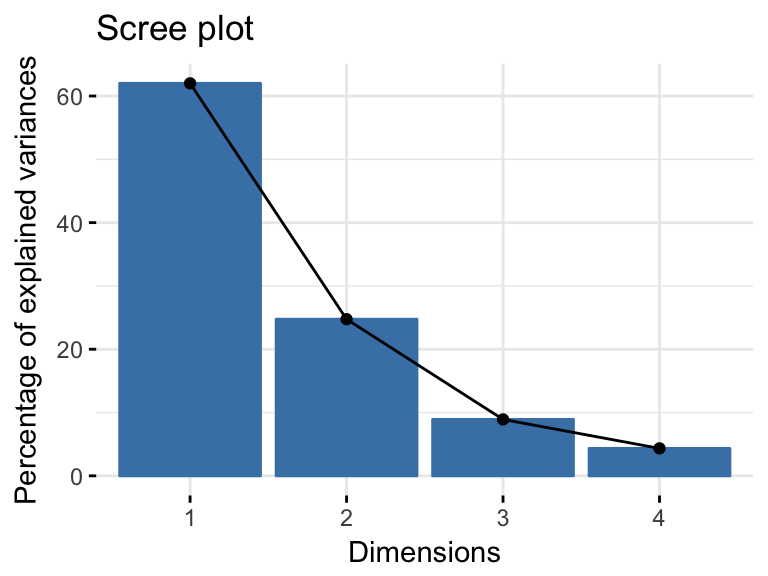
- Visualize the graph of individuals. Individuals with a similar profile are grouped together.
fviz_pca_ind(res.pca, repel = TRUE)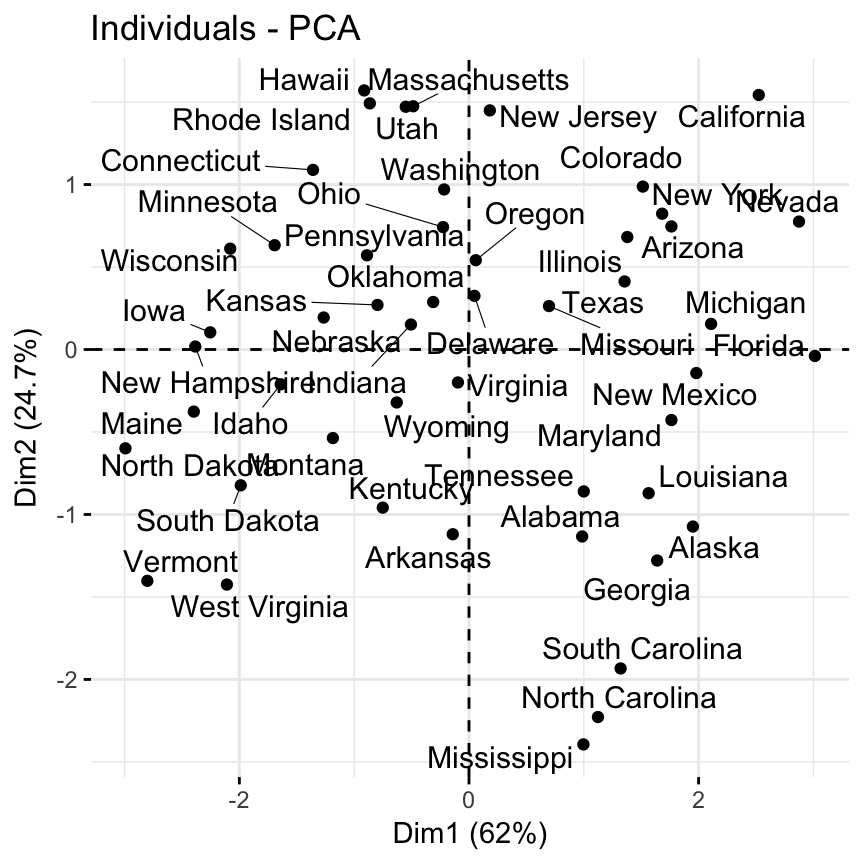
Note that dimensions (Dim) 1 and 2 retained about 87% (62% + 24.7%) of the total information contained in the data set, which is very good.
- Visualize the graph of variables. Positive correlated variables point to the same side of the plot. Negative correlated variables point to opposite sides of the graph.
fviz_pca_var(res.pca)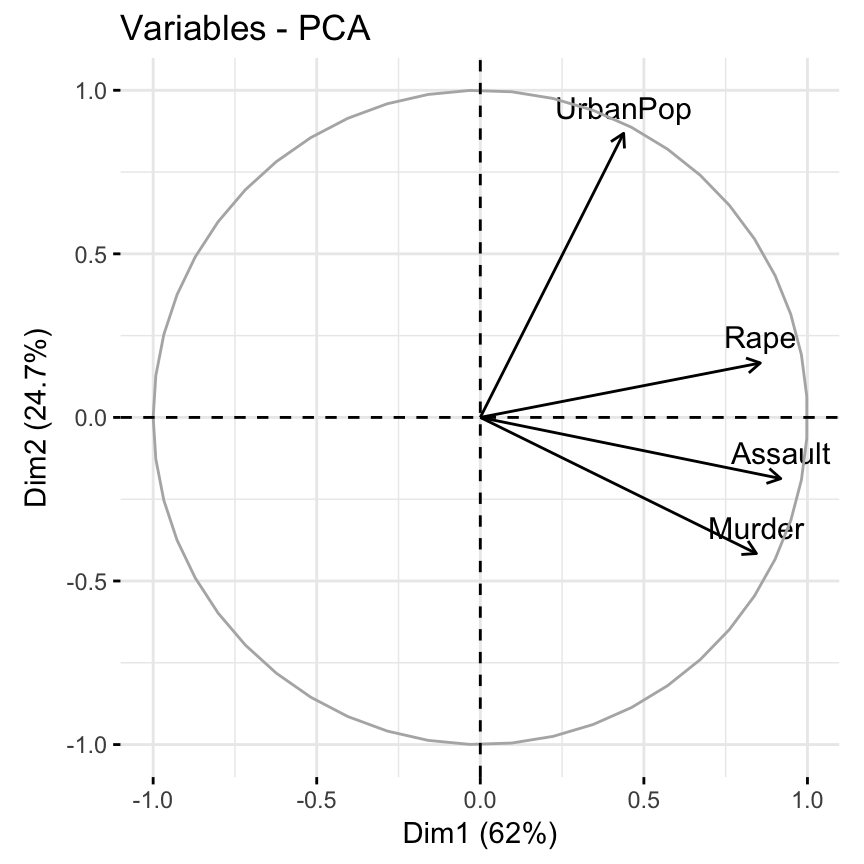
- Create a biplot of individuals and variables
fviz_pca_biplot(res.pca, repel = TRUE)- Access to the results:
# Eigenvalues
res.pca$eig
# Results for Variables
res.var <- res.pca$var
res.var$coord # Coordinates
res.var$contrib # Contributions to the PCs
res.var$cos2 # Quality of representation
# Results for individuals
res.ind <- res.pca$var
res.ind$coord # Coordinates
res.ind$contrib # Contributions to the PCs
res.ind$cos2 # Quality of representation - Read more at: Principal Component Analyis
Correspondence analysis
Correspondence analysis is an extension of the principal component analysis for analyzing a large contingency table formed by two qualitative variables (or categorical data). Like principal component analysis, it provides a solution for summarizing and visualizing data set in two-dimension plots.
The plot shows the association between row and column points of the contingency table.
- Demo data set:
Housetasks[in FactoMineR], which is a contingency table containing the frequency of execution of 13 house tasks in the couple. - Compute CA using the R function
CA()[FactoMineR] - Visualize the output using the
factoextraR package
# Load and inspect the data set
data("housetasks")
head(housetasks, 4)## Wife Alternating Husband Jointly
## Laundry 156 14 2 4
## Main_meal 124 20 5 4
## Dinner 77 11 7 13
## Breakfeast 82 36 15 7# Compute correspondence analysis
res.ca <- CA(housetasks, graph = FALSE)
fviz_ca_biplot(res.ca, repel = TRUE)
From the graphic above, it’s can be seen that:
- Housetasks such as dinner, breakfeast, laundry are done more often by the wife
- Driving and repairs are done more frequently by the husband
Read more at: Correspondence analysis in R
Multiple correspondence analysis
The Multiple correspondence analysis (MCA) is an extension of the simple correspondence analysis for summarizing and visualizing a data table containing more than two categorical variables. It can also be seen as a generalization of principal component analysis when the variables to be analyzed are categorical instead of quantitative.
MCA is generally used to analyse a data set from survey. The goal is to identify: 1) A group of individuals with similar profile in their answers to the questions; 2) The associations between variable categories
- Demo data set:
poison[in FactoMineR]. This data is a result from a survey carried out on children of primary school who suffered from food poisoning. They were asked about their symptoms and about what they ate. - Compute MCA using the R function
MCA()[FactoMineR] - Visualize the output using the
factoextraR package
# Load data
data("poison")
head(poison[, 1:8], 4)## Age Time Sick Sex Nausea Vomiting Abdominals Fever
## 1 9 22 Sick_y F Nausea_y Vomit_n Abdo_y Fever_y
## 2 5 0 Sick_n F Nausea_n Vomit_n Abdo_n Fever_n
## 3 6 16 Sick_y F Nausea_n Vomit_y Abdo_y Fever_y
## 4 9 0 Sick_n F Nausea_n Vomit_n Abdo_n Fever_nThe data contain some supplementary variables. They don’t participate to the MCA. The coordinates of these variables will be predicted.
- Supplementary quantitative variables (quanti.sup): Columns 1 and 2 corresponding to the columns age and time, respectively.
- Supplementary qualitative variables (quali.sup: Columns 3 and 4 corresponding to the columns Sick and Sex, respectively. This factor variables will be used to color individuals by groups.
Compute and visualize MCA:
# Compute multiple correspondence analysis:
res.mca <- MCA(poison, quanti.sup = 1:2,
quali.sup = 3:4, graph=FALSE)
# Graph of individuals, colored by groups ("Sick")
fviz_mca_ind(res.mca, repel = TRUE, habillage = "Sick",
addEllipses = TRUE)
# Graph of variable categories
fviz_mca_var(res.mca, repel = TRUE)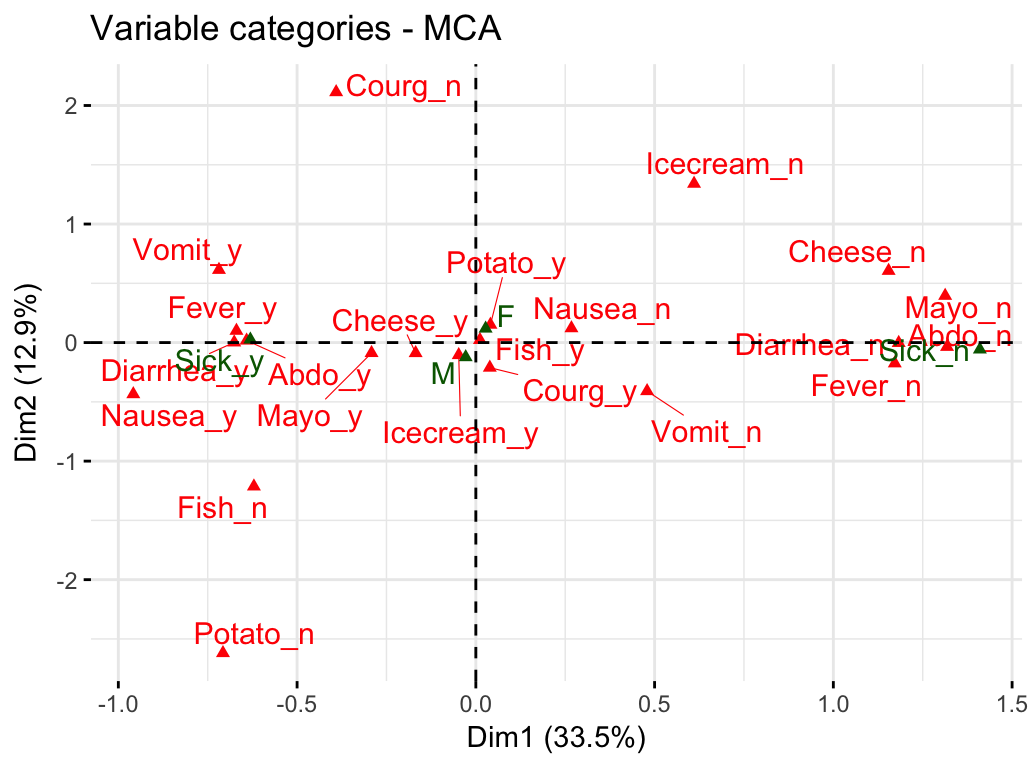
Interpretation:
- Graph of individuals: Individuals with similar profile are grouped together.
- Graph of variable categories: The plot above shows the relationships between variable categories. It can be interpreted as follow:
- Variable categories with a similar profile are grouped together.
- Negatively correlated variable categories are positioned on opposite sides of the plot origin (opposed quadrants).
- The distance between category points and the origin measures the quality of the variable category on the factor map. Category points that are away from the origin are well represented on the factor map.
Biplot of individuals and variables. The plot above shows a global pattern within the data. Rows (individuals) are represented by blue points and columns (variable categories) by red triangles. Variables and individuals that are positively associated are on the same side of the plot.
fviz_mca_biplot(res.mca, repel = TRUE,
ggtheme = theme_minimal())Read more at: Multiple Correspondence analysis
Cluster analysis
Basics
Cluster analysis is used to identify groups of similar objects in a multivariate data sets collected from fields such as marketing, bio-medical and geo-spatial. Read more at: https://www.sthda.com/english/articles/25-cluster-analysis-in-r-practical-guide/.
Type of clustering. There are different types of clustering methods, including:
- Partitioning clustering: Subdivides the data into a set of k groups.
- Hierarchical clustering: Identify groups in the data without subdividing it.
Distance measures. The classification of observations into groups requires some methods for computing the distance or the (dis)similarity between each pair of observations. The result of this computation is known as a dissimilarity or distance matrix. There are different methods for measuring distances, including:
- Euclidean distance
- Correlation based-distance
What type of distance measures should we choose? The choice of distance measures is very important, as it has a strong influence on the clustering results. For most common clustering software, the default distance measure is the Euclidean distance.
Depending on the type of the data and the researcher questions, other dissimilarity measures might be preferred.
If we want to identify clusters of observations with the same overall profiles regardless of their magnitudes, then we should go with correlation-based distance as a dissimilarity measure. This is particularly the case in gene expression data analysis, where we might want to consider genes similar when they are “up” and “down” together. It is also the case, in marketing if we want to identify group of shoppers with the same preference in term of items, regardless of the volume of items they bought.
If Euclidean distance is chosen, then observations with high values of features will be clustered together. The same holds true for observations with low values of features.
Data standardization. Before cluster analysis, it’s recommended to scale (or normalize) the data, to make the variables comparable. This is particularly recommended when variables are measured in different scales (e.g: kilograms, kilometers, centimeters, …); otherwise, the dissimilarity measures obtained will be severely affected. R function for scaling the data: scale(), applies scaling on the column of the data (variables).
Loading required R packages
clusterfor cluster analysisfactoextrafor cluster visualization
library(cluster)
library(factoextra)Data preparation
We’ll use the demo data set USArrests. We start by standardizing the data:
mydata <- scale(USArrests) Partitioning clustering
Partitioning algorithms are clustering techniques that subdivide the data sets into a set of k groups, where k is the number of groups pre-specified by the analyst.
There are different types of partitioning clustering methods. The most popular is the K-means clustering, in which, each cluster is represented by the center or means of the data points belonging to the cluster. The K-means method is sensitive to outliers.
An alternative to k-means clustering is the K-medoids clustering or PAM (Partitioning Around Medoids), which is less sensitive to outliers compared to k-means.
Read more: Partitioning Clustering methods.
The following R codes show how to determine the optimal number of clusters and how to compute k-means and PAM clustering in R.
- Determining the optimal number of clusters: use
factoextra::fviz_nbclust()
fviz_nbclust(mydata, kmeans, method = "gap_stat")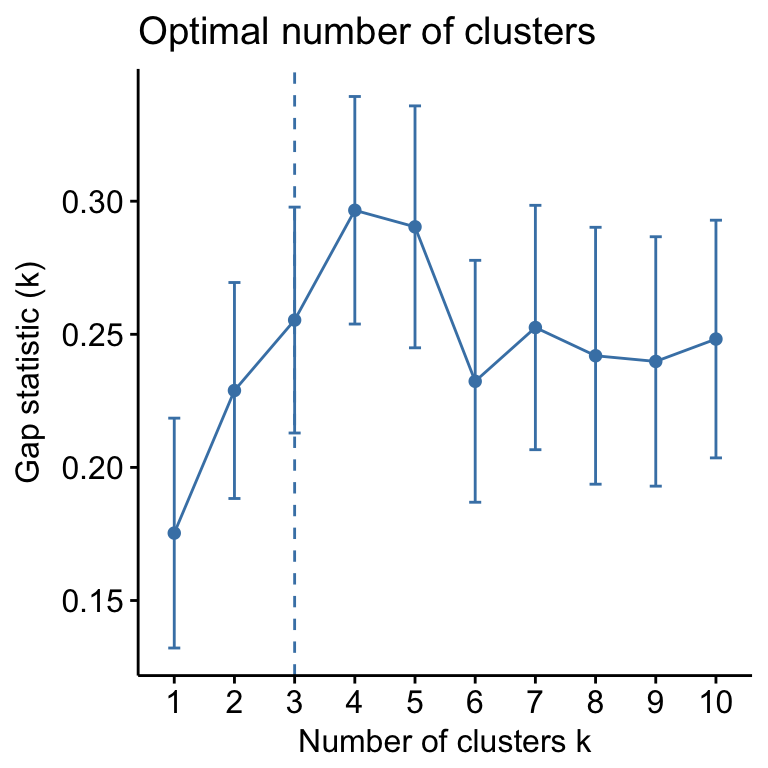
Suggested number of cluster: 3
- Compute and visualize k-means clustering:
set.seed(123) # for reproducibility
km.res <- kmeans(mydata, 3, nstart = 25)
# Visualize
fviz_cluster(km.res, data = mydata, palette = "jco",
ggtheme = theme_minimal())
- Similarly, the k-medoids/pam clustering can be computed and visualized as follow:
pam.res <- pam(mydata, 3)
fviz_cluster(pam.res)Hierarchical clustering
Hierarchical clustering is an alternative approach to partitioning clustering for identifying groups in the data set. It does not require to pre-specify the number of clusters to be generated.
The result of hierarchical clustering is a tree-based representation of the objects, which is also known as dendrogram. Observations can be subdivided into groups by cutting the dendrogram at a desired similarity level.
- Computation: R function:
hclust(). It takes a dissimilarity matrix as an input, which is calculated using the functiondist(). - Visualization:
fviz_dend()[in factoextra]
R code to compute and visualize hierarchical clustering:
res.hc <- hclust(dist(mydata), method = "ward.D2")
fviz_dend(res.hc, cex = 0.5, k = 4, palette = "jco") 
A heatmap is another way to visualize hierarchical clustering. It’s also called a false colored image, where data values are transformed to color scale. Heat maps allow us to simultaneously visualize groups of samples and features. You can easily create a pretty heatmap using the R package pheatmap.
In heatmap, generally, columns are samples and rows are variables. Therefore we start by transposing the data before creating the heatmap.
library(pheatmap)
pheatmap(t(mydata), cutree_cols = 4)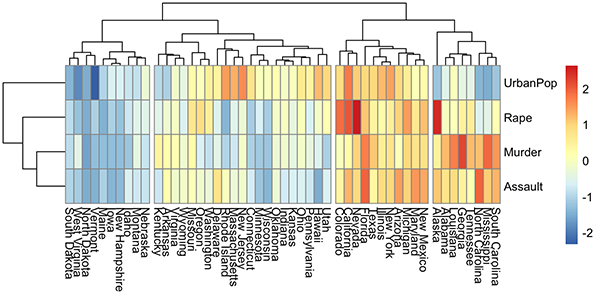
Discussion
This chapter presents the most commonly used unsupervised machine learning methods for summarizing and visualizing large multivariate data sets. You can read more on STHDA website at:



