Matrice de corrélation: Guide simple pour analyser, formater et visualiser
- C?est quoi une matrice de corr?lation?
- Analyse de corr?lation dans R
- Donn?es pour le test de corr?lation
- Matrice de corr?lation
- Test de significativit? de la corr?lation (p-value)
- Une fonction simple pour formatter la matrice de corr?lation
- Visualisation d?une matrice de corr?lation
- Logiciel en ligne pour analyser et visualiser une matrice de corr?lation
- conclusions
- Infos
C?est quoi une matrice de corr?lation?
Une matrice de corr?lation est utilis?e pour ?valuer la d?pendence entre plusieurs variables en m?me temps. Le r?sultat est une table contenant les coefficients de corr?lation entre chaque variable et les autres.
Il existe diff?rentes m?thodes de tests de corr?lation : Le test de corr?lation de Pearson, la corr?lation de Kendall et celle de Spearman qui sont des tests bas?s sur le rang. Ces m?thodes sont discut?es dans les sections suivantes.
La matrice de corr?lation peut ?tre visualis?e en utilisant un corr?logramme. L?objectif de cet article est de vous montrer comment calculer et visualiser une matrice de corr?lation dans R.
Analyse de corr?lation dans R
Comme vous le savez peut ?tre, la fonction cor() de R peut ?tre utilis?e pour calculer la matrice de corr?lation. Un format simplifi? de la fonction est :
# x est une variable de type matrix ou data.frame
cor(x, method = c("pearson", "kendall", "spearman"))L?argument method indique le type de coefficient de corr?lation ? calculer. La valeur par d?faut est le coefficient de corr?lation de pearson, lequel mesure une d?pendence lin?aire entre deux variables. Les m?thodes de corr?lation kendall et spearman sont des tests de corr?lation non-param?triques bas?s sur un test de rang.
Donn?es pour le test de corr?lation
La table de donn?es mtcars disponible dans R est utilis?e dans les exemples suivants pour calculer la matrice de corr?lation.
data(mtcars)
head(mtcars) mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1Matrice de corr?lation
mcor <- cor(mtcars)
mcor mpg cyl disp hp drat wt qsec vs am gear carb
mpg 1.00 -0.85 -0.85 -0.78 0.68 -0.87 0.42 0.66 0.60 0.48 -0.55
cyl -0.85 1.00 0.90 0.83 -0.70 0.78 -0.59 -0.81 -0.52 -0.49 0.53
disp -0.85 0.90 1.00 0.79 -0.71 0.89 -0.43 -0.71 -0.59 -0.56 0.39
hp -0.78 0.83 0.79 1.00 -0.45 0.66 -0.71 -0.72 -0.24 -0.13 0.75
drat 0.68 -0.70 -0.71 -0.45 1.00 -0.71 0.09 0.44 0.71 0.70 -0.09
wt -0.87 0.78 0.89 0.66 -0.71 1.00 -0.17 -0.55 -0.69 -0.58 0.43
qsec 0.42 -0.59 -0.43 -0.71 0.09 -0.17 1.00 0.74 -0.23 -0.21 -0.66
vs 0.66 -0.81 -0.71 -0.72 0.44 -0.55 0.74 1.00 0.17 0.21 -0.57
am 0.60 -0.52 -0.59 -0.24 0.71 -0.69 -0.23 0.17 1.00 0.79 0.06
gear 0.48 -0.49 -0.56 -0.13 0.70 -0.58 -0.21 0.21 0.79 1.00 0.27
carb -0.55 0.53 0.39 0.75 -0.09 0.43 -0.66 -0.57 0.06 0.27 1.00Dans la table ci-dessus les coefficients de corr?lation sont montr?s entre les diff?rentes paires possibles de variables.
Si vos donn?es contiennent des valeurs manquantes, utiliser le code R suivant qui va automatiquement les g?rer en les supprimant.
cor(mtcars, use = "complete.obs")Test de significativit? de la corr?lation (p-value)
Le r?sultat de la fonction cor() est une table de coefficients de corr?lation entre chaque variable et les autres. Malheureusement, cette fonction n?affiche pas la significativit? de la corr?lation (p-value). Dans la section suivante, nous allons utiliser le package Hmisc de R pour calculer la p-value de la corr?lation.
La fonction rcorr() du package Hmisc peut ?tre utilis?e pour calculer le niveau de significativit? pour les corr?lations de pearson et de spearman. En utilisant cette fonction le coefficient de corr?lation r de Pearson ou rho de Spearman est calculer pour toutes les paires de variables possibles dans la table de donn?es.
Un format simplifi? de la fonction est:
rcorr(x, type=c("pearson","spearman"))x doit ?tre un objet de type matrix. Le type de corr?lation peut ?tre soit pearson ou spearman.
library(Hmisc)
rcorr(as.matrix(mtcars[,1:7])) mpg cyl disp hp drat wt qsec
mpg 1.00 -0.85 -0.85 -0.78 0.68 -0.87 0.42
cyl -0.85 1.00 0.90 0.83 -0.70 0.78 -0.59
disp -0.85 0.90 1.00 0.79 -0.71 0.89 -0.43
hp -0.78 0.83 0.79 1.00 -0.45 0.66 -0.71
drat 0.68 -0.70 -0.71 -0.45 1.00 -0.71 0.09
wt -0.87 0.78 0.89 0.66 -0.71 1.00 -0.17
qsec 0.42 -0.59 -0.43 -0.71 0.09 -0.17 1.00
n= 32
P
mpg cyl disp hp drat wt qsec
mpg 0.0000 0.0000 0.0000 0.0000 0.0000 0.0171
cyl 0.0000 0.0000 0.0000 0.0000 0.0000 0.0004
disp 0.0000 0.0000 0.0000 0.0000 0.0000 0.0131
hp 0.0000 0.0000 0.0000 0.0100 0.0000 0.0000
drat 0.0000 0.0000 0.0000 0.0100 0.0000 0.6196
wt 0.0000 0.0000 0.0000 0.0000 0.0000 0.3389
qsec 0.0171 0.0004 0.0131 0.0000 0.6196 0.3389 Comme r?sultat, la fonction rcorr() renvoie une liste avec les ?l?ments suivants : - r : la matrice de corr?lation. - n : la matrice du nombre d?observations utilis? dans l?analyse de chaque paire de variables. - P : les p-values correspondant aux niveaux de significativit? des corr?lations.
Une fonction simple pour formatter la matrice de corr?lation
Cette section fournit une fonction simple pour formater une matrice de corr?lation en une table ? 4 colonnes contenant :
- Colonne 1 : Noms des lignes (variable 1 pour le test de corr?lation)
- Colonne 2 : Nom des colonnes (variable 2 pour le test de corr?lation)
- Colonne 3 : Les coefficients de corr?lation
- Colonne 4 : Les p-values des corr?lations
La fonction ci-dessous peut ?tre utilis?e:
# ++++++++++++++++++++++++++++
# flattenCorrMatrix
# ++++++++++++++++++++++++++++
# cormat : matrix of the correlation coefficients
# pmat : matrix of the correlation p-values
flattenCorrMatrix <- function(cormat, pmat) {
ut <- upper.tri(cormat)
data.frame(
row = rownames(cormat)[row(cormat)[ut]],
column = rownames(cormat)[col(cormat)[ut]],
cor =(cormat)[ut],
p = pmat[ut]
)
}Exemple d?utilisation :
library(Hmisc)
res<-rcorr(as.matrix(mtcars[,1:7]))
flattenCorrMatrix(res$r, res$P) row column cor p
1 mpg cyl -0.8522 6.113e-10
2 mpg disp -0.8476 9.380e-10
3 cyl disp 0.9020 1.803e-12
4 mpg hp -0.7762 1.788e-07
5 cyl hp 0.8324 3.478e-09
6 disp hp 0.7909 7.143e-08
7 mpg drat 0.6812 1.776e-05
8 cyl drat -0.6999 8.245e-06
9 disp drat -0.7102 5.282e-06
10 hp drat -0.4488 9.989e-03
11 mpg wt -0.8677 1.294e-10
12 cyl wt 0.7825 1.218e-07
13 disp wt 0.8880 1.222e-11
14 hp wt 0.6587 4.146e-05
15 drat wt -0.7124 4.784e-06
16 mpg qsec 0.4187 1.708e-02
17 cyl qsec -0.5912 3.661e-04
18 disp qsec -0.4337 1.314e-02
19 hp qsec -0.7082 5.766e-06
20 drat qsec 0.0912 6.196e-01
21 wt qsec -0.1747 3.389e-01Visualisation d?une matrice de corr?lation
Plusieurs solutions sont disponibles dans R pour visualiser une matrice de corr?lation:
- la fonction symnum()
- la fonction corrplot() pour dessiner un correlogramme
- le Nuage de points (scatter plots)
- heatmap
Visualiser une matrice de corr?lation avec la fonction symnum
La fonction symnum de R remplace les coefficients de corr?lation par des symboles en fonction de leurs valeurs. Elle prend la matrice de corr?lation comme argument:
symnum(mcor, abbr.colnames=FALSE) mpg cyl disp hp drat wt qsec vs am gear carb
mpg 1
cyl + 1
disp + + 1
hp , + , 1
drat , , , . 1
wt + , + , , 1
qsec . . . , 1
vs , + , , . . , 1
am . . . , , 1
gear . . . , . , 1
carb . . . , . , . 1
attr(,"legend")
[1] 0 ' ' 0.3 '.' 0.6 ',' 0.8 '+' 0.9 '*' 0.95 'B' 1Comme indiqu? dans la l?gende, les coefficients de corr?lation entre 0 et 0.3 sont remplac?s par un espace (" ?); les coefficients de corr?lation entre 0.3 et 0.6 sont remplac?s par?.?; etc ?
Visualiser une matrice de corr?lation avec un corr?logramme
Vous devez installer le package corrplot qui permet de faire une visualisation graphique de la matrice de corr?lation.
Pour lire plus ? propos de la fonction corplot() cliquez ici : visualiser une matrice de corr?lation avec la fonction corrplot.
La fonction corrplot prend la matrice de corr?lation comme premier argument. Le second argument (type=?upper?) est utilis? pour afficher seulement le triangle sup?rieur de la matrice de corr?lation.
library(corrplot)
corrplot(mcor, type="upper", order="hclust", tl.col="black", tl.srt=45)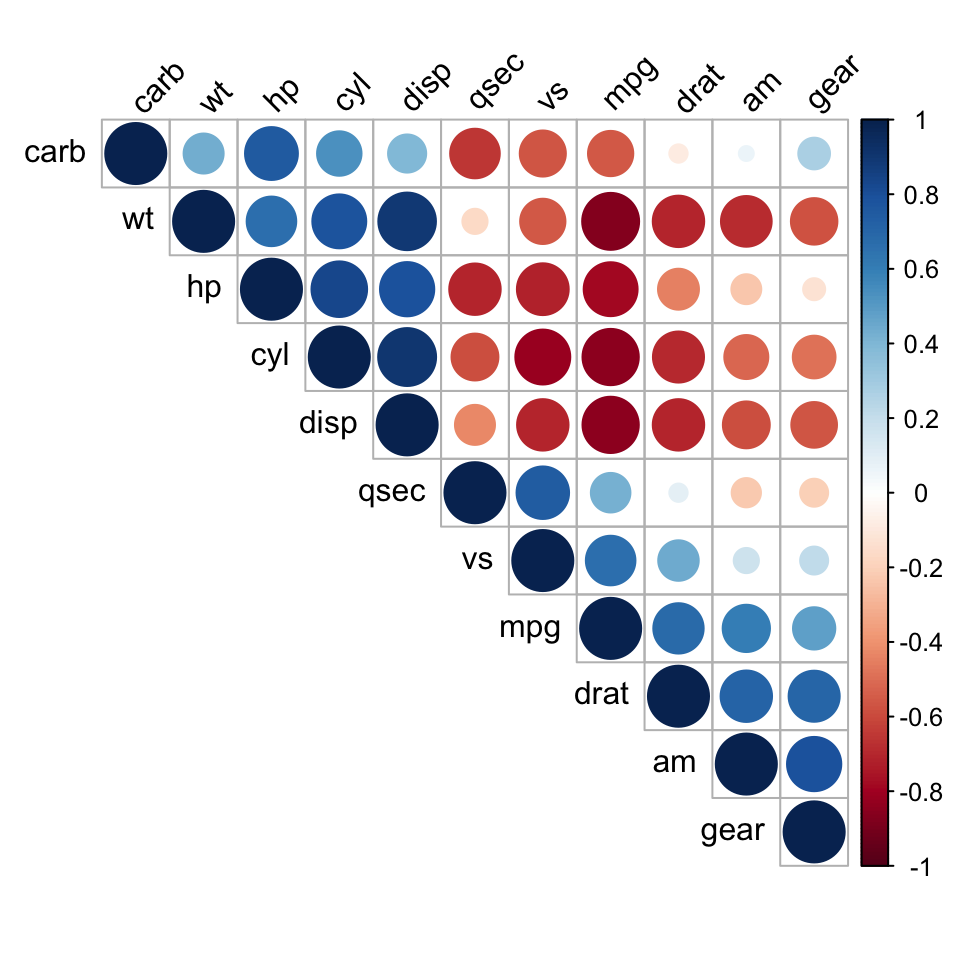
Les corr?lations positives sont affich?es en bleu et les corr?lations n?gatives en rouge. L?intensit? de la couleur et la taille des cercles sont proportionnelles aux coefficients de corr?lation. A droite du corr?logramme, la l?gende de couleurs montre les coefficients de corr?lation et les couleurs correspondantes.
La matrice de corr?lation est r?arrang?e en fonction des coefficients de corr?lation en utilisant la m?thode hclust. tl.col (text label color) et tl.srt (text label string rotation) sont utilis?s pour changer la couleur et la rotation des ?tiquettes de textes.
Visualiser une matrice de corr?lation avec des scatter plots
La fonction chart.Correlation(), du package PerformanceAnalytics, peut ?tre utilis?e pour faire un graphique de la matrice de corr?lation. Installer le package si vous ne l?avez pas d?j?.
library(PerformanceAnalytics)
mydata <- mtcars[, c(1,3,4,5,6,7)]
chart.Correlation(mydata, histogram=TRUE, pch=19)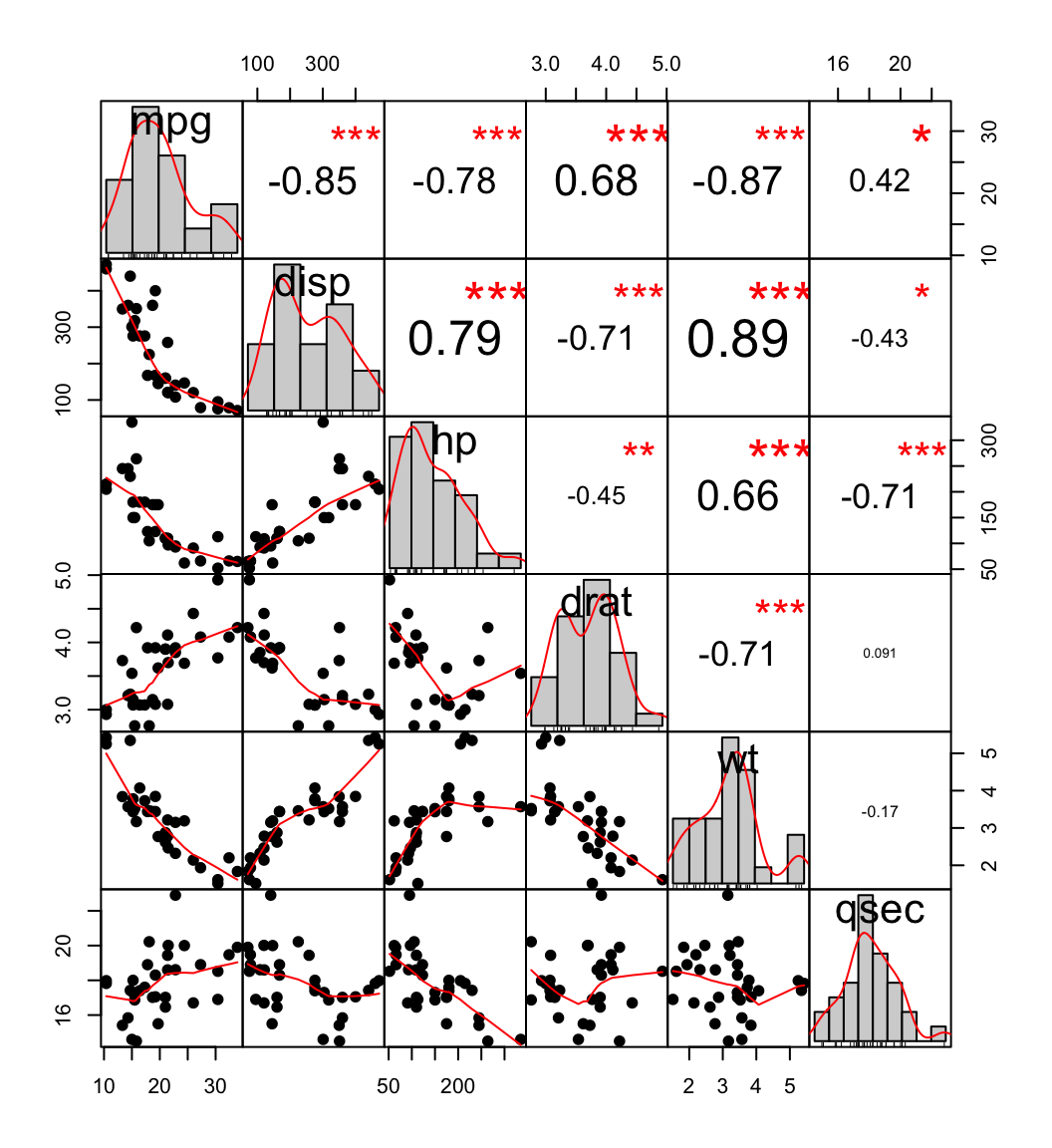
- La distribution de chaqu?un des variables est montr? sur la diagonale.
- En bas de la diagonale : Les scatter plots sont montr?s avec la courbe de tendance
- En haut de la diagonale : Les coefficients de corr?lation et les niveaux de significativit? (?toiles) sont montr?s
Chaque niveau de significativit? est associ? ? un symbole :
p-values(0, 0.001, 0.01, 0.05, 0.1, 1) <=> symboles(?***?, ?**?, ?*?, ?.?, " ?)
Visualiser une matrice de corr?lation avec un heatmap
# G?n?rer des couleurs
col<- colorRampPalette(c("blue", "white", "red"))(20)
heatmap(x = mcor, col = col, symm = TRUE)
- x : la matrice de corr?lation ? dessiner
- col : palettes de couleurs
- symm : valeur logique indiquant si x devrait ?tre trait? comme sym?trique; peut ?tre true si seulement si x est une matrice carr?e.
Logiciel en ligne pour analyser et visualiser une matrice de corr?lation
Une application web pour calculer et visualiser une matrice de corr?lation est disponible ici sans aucune installation: logiciel en ligne de calcul de matrices de corr?lation.
Acc?der au logiciel de calcul de matrices de corr?lation
Le logiciel peut ?tre utilis? comme suit :
- Acc?der au logiciel web de calcul de matrices de corr?lation : calculateur de matrices de corr?lation
- Charger un fichier .txt tabulation ou CSV contenant vos donn?es (les colonnes sont les variables). Les formats de fichiers support?s sont d?crits ici. Vous pouvez utiliser les donn?es de d?mo disponibles sur la page Web du logiciel en cliquant sur le lien correspondant.
- Apr?s chargement, un aper?u d?une partie de votre fichier est affich? pour v?rifier que les donn?es sont correctement import?es. Si les donn?es ne sont pas affich?es correctement, assurez-vous que le format de votre fichier est correct ici.
- Cliquez sur le bouton ?Analyser? et s?lectionner au moins deux variables pour calculer la matrice de corr?lation. Par d?faut, toutes les variables sont s?lectionn?es. D?s?lectionner les colonnes contenant du texte. Vous pouvez ?galement s?lectionner les m?thodes de corr?lation (Pearson, Spearman ou de Kendall). Par d?faut la m?thode de Pearson est choisie.
- Cliquer sur le bouton Ok
- R?sultats : la sortie du logiciel comprend :
- La matrice de corr?lation
- La visualisation de la matrice de corr?lation en corr?logramme
- Un lien web pour exporter les r?sultats dans un fichier .txt
Notez que, vous pouvez sp?cifier l?hypoth?se alternative ? utiliser pour le test de corr?lation en cliquant sur le bouton ?Options avanc?es?.
Choisissez l?une des 3 options ci-dessous :
- Two-sided pour un test bilat?ral
- Corr?lation <0 pour un test unilat?ral inf?rieur
- Corr?lation > 0 pour un test unilat?ral sup?rieur
conclusions
- Utiliser la fonction cor() pour une simple analyse de corr?lation
- Utiliser la fonction rcorr() du package Hmisc pour calculer la matrice de coefficients de corr?lation ainsi que la matrice de p-value en une seule ?tape.
- Utiliser la fonction symnum() ou corplot()[du package R corrplot] pour faire le graphique de la matrice de corr?lation.
Infos
Cette analyse a ?t? faite avec R (ver. 3.1.0).
Show me some love with the like buttons below... Thank you and please don't forget to share and comment below!!
Montrez-moi un peu d'amour avec les like ci-dessous ... Merci et n'oubliez pas, s'il vous plaît, de partager et de commenter ci-dessous!
Recommended for You!
Click to follow us on Facebook:
Comment this article by clicking on "Discussion" button (top-right position of this page)








