Visualiser une matrice de corrélation par un corrélogramme
- Introduction
- Installer le package corrplot
- Données pour l'analyse de corrélation
- Calcul de la matrice de corrélation
- Corrélogramme : Visualisation de la matrice de corrélation
- Méthodes de visualisation
- Les différentes dispositions du corrélogrammes
- Réordonner la matrice de corrélation
- Changement de la couleur du corrélogramme
- Changement de la couleur et de la rotation des étiquettes de textes
- Combiner le corrélogramme avec le test de significativité
- Personnaliser le corrélogramme
- Conclusions
- Infos
Introduction
Cet article décrit comment dessiner un corrélogramme dans R. Un corrélogramme représente le graphique d'une matrice de corrélation. Le corrélogramme est très important pour mettre en évidence les variables les plus corrélées. Dans ce type de graphique, les coefficients de corrélation sont colorés en fonction de leur valeur. La matrice de corrélation peut être aussi réordonnée en fonction du degré de corrélation entre les variables. Le package corrplot de R est utilisé dans ce document.
Installer le package corrplot
Le package corrplot est nécessaire pour exécuter le code R dans cet article.
install.packages("corrplot")Données pour l'analyse de corrélation
La table de données mtcars est utilisée pour calculer la matrice de corrélation.
head(mtcars) mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1Calcul de la matrice de corrélation
M<-cor(mtcars)
head(round(M,2)) mpg cyl disp hp drat wt qsec vs am gear carb
mpg 1.00 -0.85 -0.85 -0.78 0.68 -0.87 0.42 0.66 0.60 0.48 -0.55
cyl -0.85 1.00 0.90 0.83 -0.70 0.78 -0.59 -0.81 -0.52 -0.49 0.53
disp -0.85 0.90 1.00 0.79 -0.71 0.89 -0.43 -0.71 -0.59 -0.56 0.39
hp -0.78 0.83 0.79 1.00 -0.45 0.66 -0.71 -0.72 -0.24 -0.13 0.75
drat 0.68 -0.70 -0.71 -0.45 1.00 -0.71 0.09 0.44 0.71 0.70 -0.09
wt -0.87 0.78 0.89 0.66 -0.71 1.00 -0.17 -0.55 -0.69 -0.58 0.43Corrélogramme : Visualisation de la matrice de corrélation
La fonction corrplot est utilisée pour faire le graphique de la **matrice de corrélation.
Le format simplifié de la fonction est:
corrplot(corr, method="circle")| Arguments | Description |
|---|---|
| corr | La matrice de corrélation à visualiser. Pour visualiser une matrice quelconque, utiliser is.corr=FALSE. |
| method | Méthodes de visualisation : "circle", "color", "number", etc. |
Méthodes de visualisation
Sept méthodes de visualisation différentes peuvent être utilisées : "circle", "square", "ellipse", "number", "shade", "color", "pie".
library(corrplot)
corrplot(M, method="circle")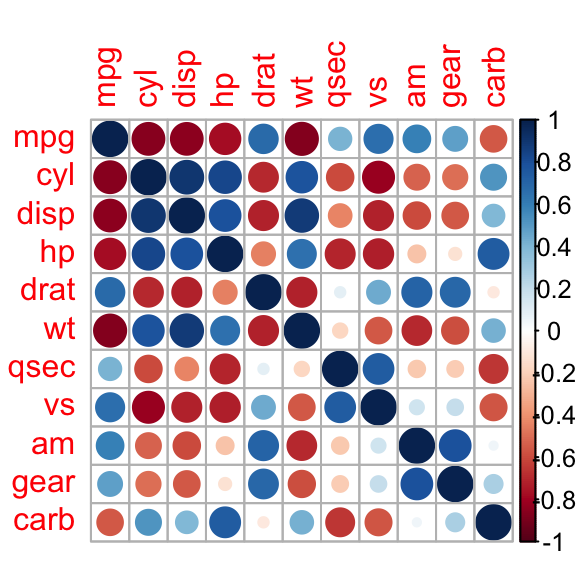
corrplot(M, method="pie")
corrplot(M, method="color")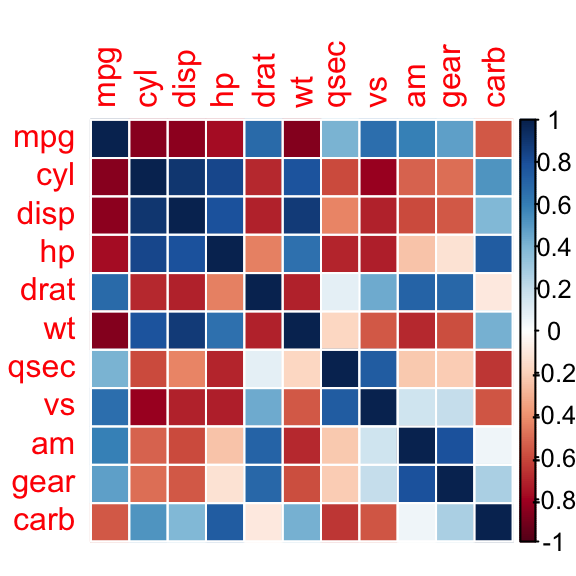
Les corrélations positives sont affichées en bleu et les corrélations négatives en rouge. L'intensité de la couleur et la taille des cercles sont proportionnelles aux coefficients de corrélation. A droite du corrélogramme, la légende de couleurs montre les coefficients de corrélation et les couleurs correspondantes.
Afficher les coefficients de corrélation :
corrplot(M, method="number")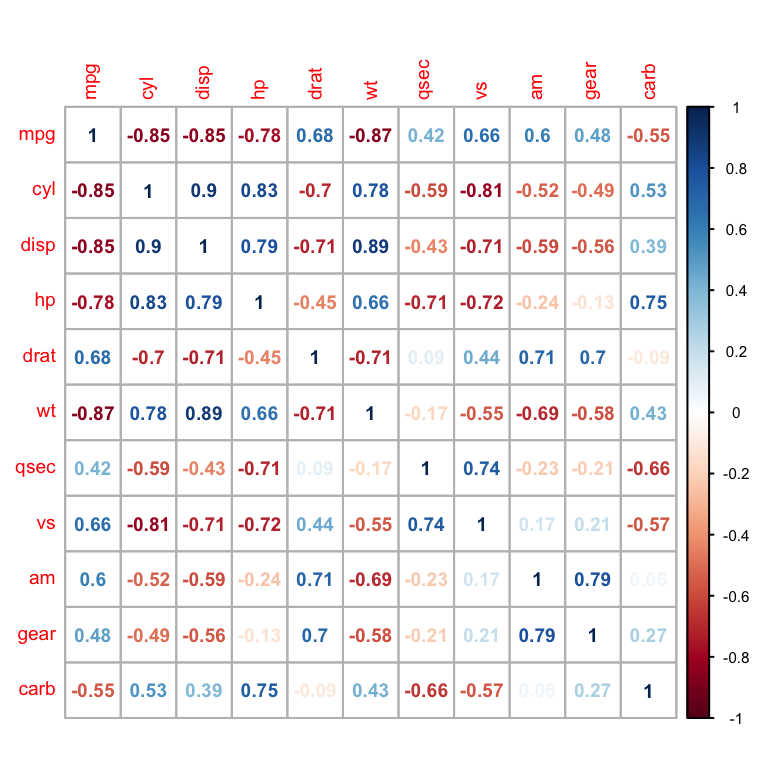
Les différentes dispositions du corréllogrammes
Il y a 3 dispositions différentes :
- full (par défaut) : Affiche la Matrice de corrélation en entier.
- upper: Affiche le triangle supérieur de la matrice de corrélation.
- lower: Affiche le triangle inférieur de la matrice de corrélation.
corrplot(M, type="upper")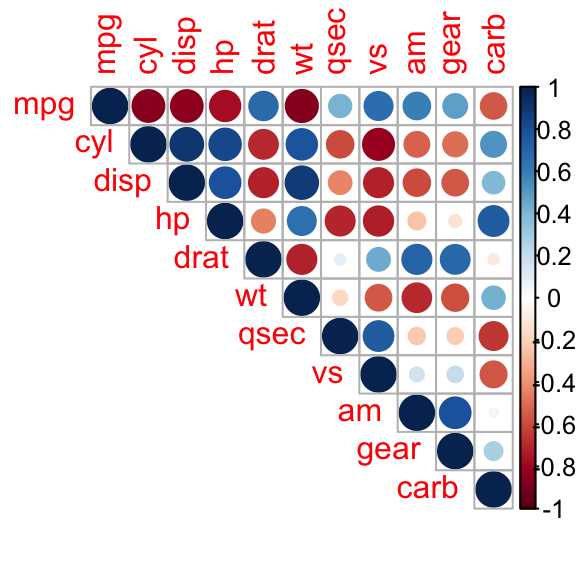
corrplot(M, type="lower")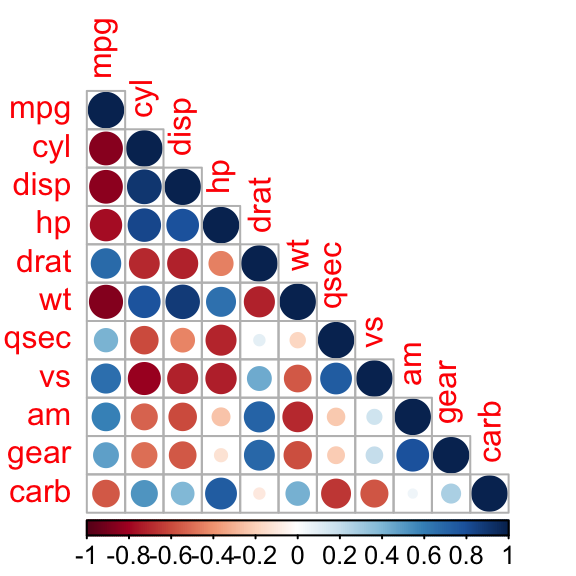
Réordonner la matrice de corrélation
La matrice de corrélation peut être réordonnée en fonction du coefficient de corrélation. Ceci est important pour identifier des profils cachés dans la matrice. La méthode hclust (pour hierarchical clustering) est utilisée dans les exemples ci-dessous.
# Corrélogramme avec réarrangement de type hclust
corrplot(M, type="upper", order="hclust")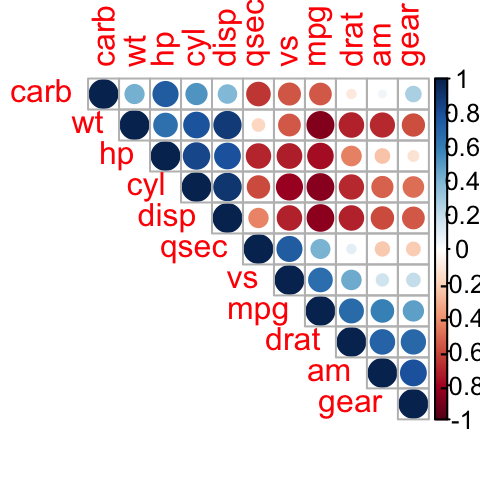
# Utilisation de différents spectres de couleurs
col<- colorRampPalette(c("red", "white", "blue"))(20)
corrplot(M, type="upper", order="hclust", col=col)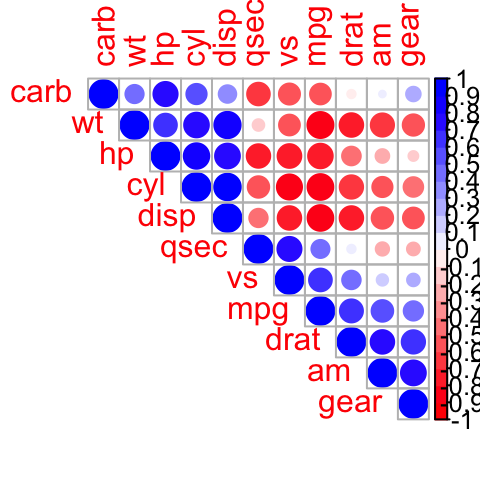
# Changer la couleur de fond en lightblue
corrplot(M, type="upper", order="hclust", col=c("black", "white"),
bg="lightblue")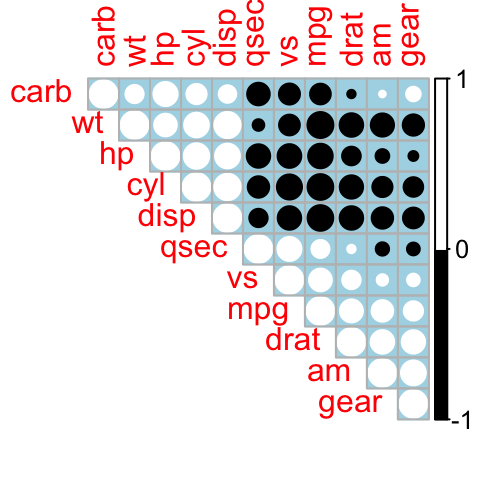
Changement de la couleur du corrélogramme
Comme montré dans les sections ci-dessus, la couleur du corrélogramme peut être personnalisée. Les palettes de couleurs du package RcolorBrewer sont utilisées dans le script ci-dessous :
library(RColorBrewer)
corrplot(M, type="upper", order="hclust",
col=brewer.pal(n=8, name="RdBu"))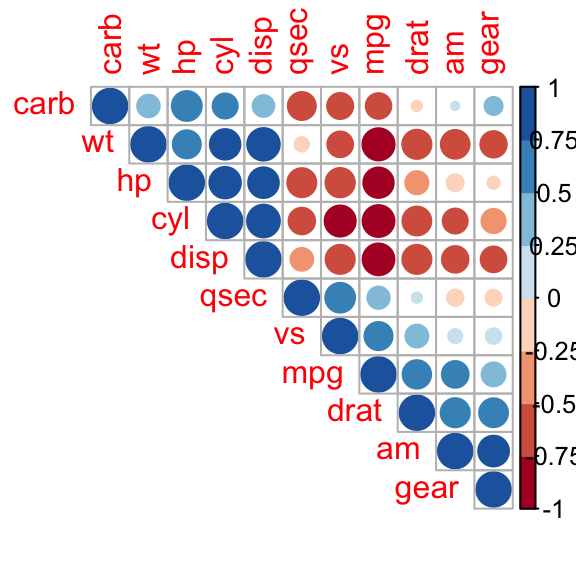
corrplot(M, type="upper", order="hclust",
col=brewer.pal(n=8, name="RdYlBu"))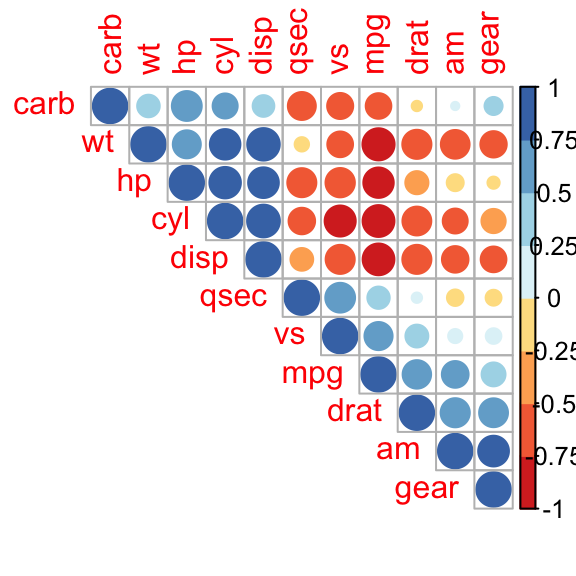
corrplot(M, type="upper", order="hclust",
col=brewer.pal(n=8, name="PuOr"))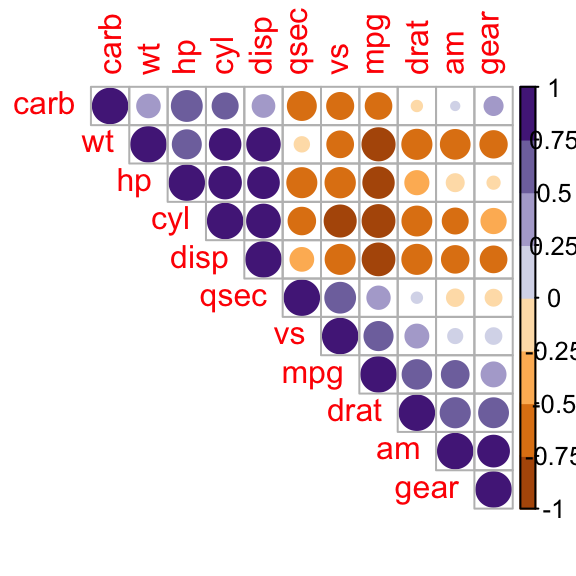
Changement de la couleur et de la rotation des étiquettes de textes
tl.col (for text label color) et tl.srt (for text label string rotation) sont utilisés pour changer la couleur et l’angle de rotation des textes.
corrplot(M, type="upper", order="hclust", tl.col="black", tl.srt=45)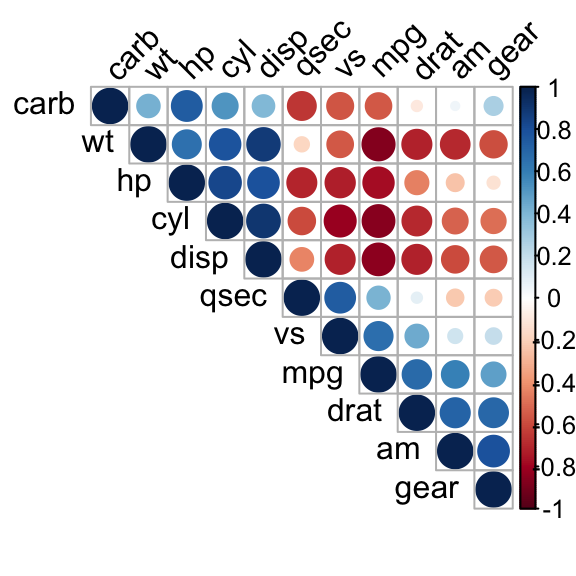
Combiner le corrélogramme avec le test de significativité
Calcul de la p-value des corrélations
Pour calculer la p-value des matrices, nous allons utiliser une fonction personnalisée:
# mat : matrice de donnée
# ... : Arguments supplémentaire à passer à la fonction cor.test
cor.mtest <- function(mat, ...) {
mat <- as.matrix(mat)
n <- ncol(mat)
p.mat<- matrix(NA, n, n)
diag(p.mat) <- 0
for (i in 1:(n - 1)) {
for (j in (i + 1):n) {
tmp <- cor.test(mat[, i], mat[, j], ...)
p.mat[i, j] <- p.mat[j, i] <- tmp$p.value
}
}
colnames(p.mat) <- rownames(p.mat) <- colnames(mat)
p.mat
}
# Matrice de p-value de la corrélation
p.mat <- cor.mtest(mtcars)
head(p.mat[, 1:5]) mpg cyl disp hp drat
mpg 0.000e+00 6.113e-10 9.380e-10 1.788e-07 1.776e-05
cyl 6.113e-10 0.000e+00 1.803e-12 3.478e-09 8.245e-06
disp 9.380e-10 1.803e-12 0.000e+00 7.143e-08 5.282e-06
hp 1.788e-07 3.478e-09 7.143e-08 0.000e+00 9.989e-03
drat 1.776e-05 8.245e-06 5.282e-06 9.989e-03 0.000e+00
wt 1.294e-10 1.218e-07 1.222e-11 4.146e-05 4.784e-06Ajout du niveau de significativité au corrélogramme
# Indication des corrélations non significatives
#par une croix
corrplot(M, type="upper", order="hclust",
p.mat = p.mat, sig.level = 0.01)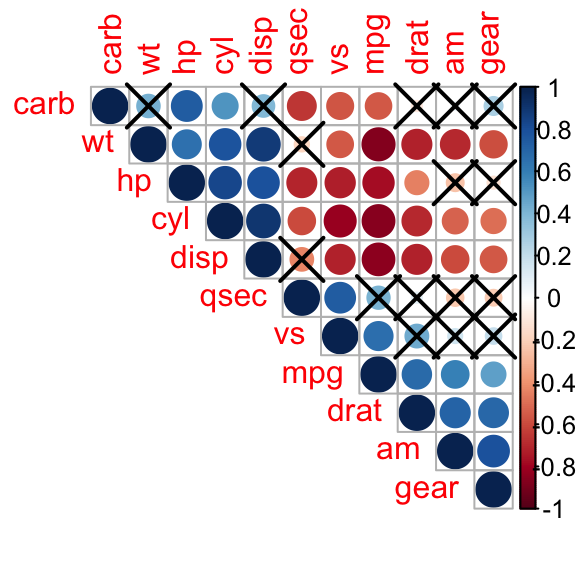
# Remplacement des corrélations non significatives
#par du blanc
corrplot(M, type="upper", order="hclust",
p.mat = p.mat, sig.level = 0.01, insig = "blank")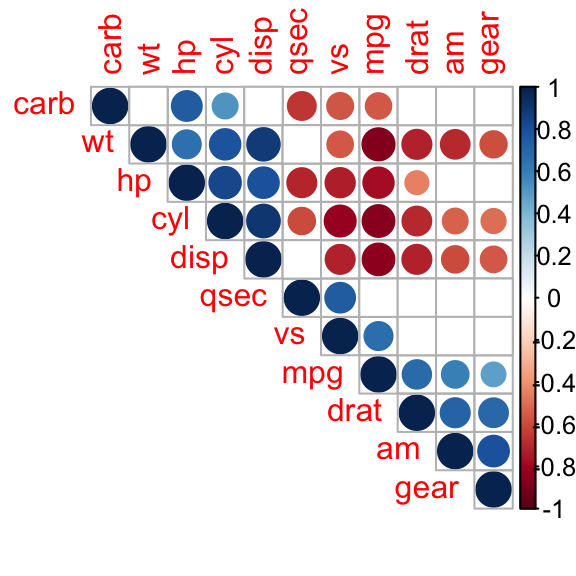
Dans la figure ci-dessus, les corrélations avec une p-value > 0.01 sont considérées comme non significatives. Dans ce cas les valeurs du coefficient de corrélation sont remplacées par du blanc ou barrées par une croix.
Personnaliser le corrélogramme
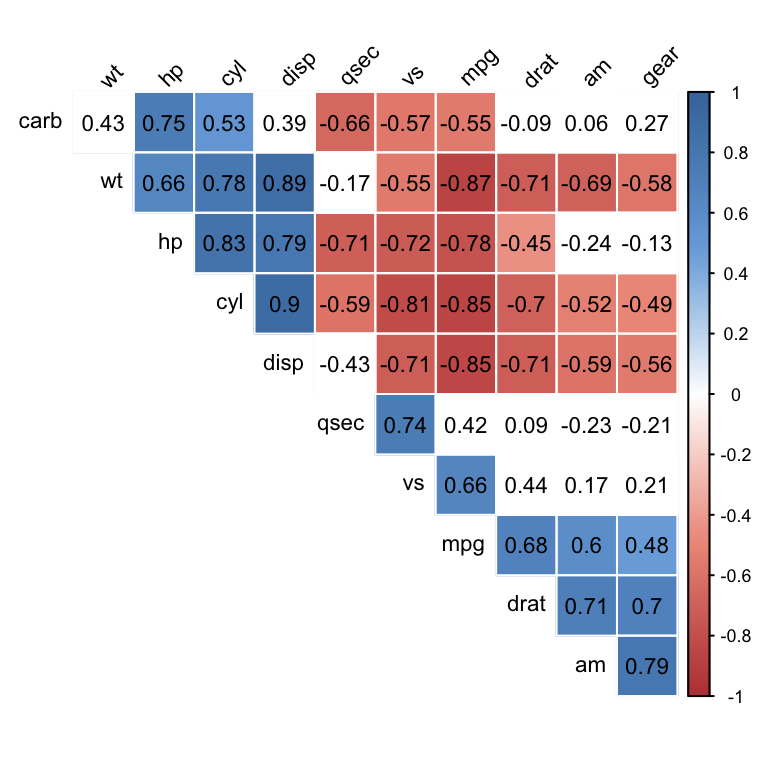
col <- colorRampPalette(c("#BB4444", "#EE9988", "#FFFFFF", "#77AADD", "#4477AA"))
corrplot(M, method="color", col=col(200),
type="upper", order="hclust",
addCoef.col = "black", # Ajout du coefficient de corrélation
tl.col="black", tl.srt=45, #Rotation des étiquettes de textes
# Combiner avec le niveau de significativité
p.mat = p.mat, sig.level = 0.01, insig = "blank",
# Cacher les coefficients de corrélation sur la diagonale
diag=FALSE
)
Conclusions
Show me some love with the like buttons below... Thank you and please don't forget to share and comment below!!
Montrez-moi un peu d'amour avec les like ci-dessous ... Merci et n'oubliez pas, s'il vous plaît, de partager et de commenter ci-dessous!
Recommended for You!
Click to follow us on Facebook:
Comment this article by clicking on "Discussion" button (top-right position of this page)







