Analyse en composante principale-Cours Poster un commentaire
Analyse en composante principale
Sommaire
- Analyse en composante principale
- Exemples
- Tableau de donn?es
- Nuage de points : R?lation entre les variables
- Valeurs propres
- Plan des variables
- Plan des individus
- Contribution des individus aux composantes en %
- Repr?sentation 3D
- Les individus supplementaires
- Les variables suppl?mentaires ou illustratifs
- Repr?sentation des individus dans le plan en fonction de leur groupe
- R?f?rences
Logiciels
 Ce logiciel d'interface graphique a ?t? r?alis? en combinant R/C++/QT.
Il vous offre la possibilit? de faire :
Ce logiciel d'interface graphique a ?t? r?alis? en combinant R/C++/QT.
Il vous offre la possibilit? de faire :
- une ACP
- une R?pr?sentation graphique du plan des individus en 2D et 3D
- R?pr?sentation graphique des variables - cercle de corr?lation
- Pr?diction de la position d' individus ou de variables suppl?mentaires n'ayant pas particip?s ? l'ACP
- G?n?ration d'un fichier txt contenant le details de l'ACP
- G?n?ration d'un fichier pdf contenant les graphiques.
Principe
L'ACP permet de synth?tiser l'information contenue dans un tableau de donn?es (n colonnes * p lignes). Elle permet d'identifier une ?ventuelle similarit? entre les individus et de determiner la liaison entre les variables.
Les donn?es sont tout d'abord centr?es et r?duites c'est ? dire que chaque variable a une moyenne =0 et un ?cart type = 1.
Notion de composante principale et de valeurs propres ou de pourcentage d'inertie
Lorsque l'on a un tableau contenant n variables, ceci correspond ? n axes (n dimensions) sous lesquels il faut representer les individus. Le principe de l'ACP consiste ? projetter les donn?es dans un espace de dimensions inferieures permettant une analyse facile des donn?es. Il faut donc remplacer les n anciens axes par de nouveaux axes. Ces nouveaux axes (Ck) sont appel?s composantes principales et s'expriment comme une combinaison linaire des anciens axes (anciennes variables). Ck = ak1x1 +ak2x2 .......+ akmxm - Les coefficients de ces combinaisons lin?aires sont fournis par le logiciel; c'est eux qui d?finissent les nouveaux axes :
- ils permettent de calculer les nouvelles coordonn?es d'un point-individu ? partir des anciennes
- ils permettent ?galement de voir le poids d'une ancienne variable dans la d?finition d'un facteur. Le rep?rage des variable d'origine correspondant aux coefficients les plus ?lev?s en valeur absolu permet de d?gager une interpr?tation des facteurs.
Choix des composantes principales
Le pr?mier axe principal est l'axe suivant lequel on a la plus grande dipersion du nuage de points (le plus grand allongement du nuage de points), permettant de distinguer au mieux les points. On dit en terme statistique, que c'est l'axe qui a la plus grande variance ou pourcentage d'inertie. La variance ou l'inertie d'un axe principal est encore appel?e valeur propre. Le 2?me axe principal, est la 2e direction d'allongement du nuage. C'est celui qui a la plus grande inertie r?siduelle apr?s la pr?mi?re composante. Ainsi de suite jusqu'? remplacer les n axes anciens par m axes nouveaux.
Pourcentage d'inertie : valeurs propres ou variances associ?es aux axes
Le pourcentage d'inertie ou de dipersion repr?sente la quantit? d'information recueillie par un axe principal. L'analyse ACP es pertinent lorsqu'on arrive avec un petit nombre d'axes ? synth?tiser le maximum de l'information (80% de l'information par exemple). En g?n?ral on poursuit l'analyse si on arrive avec 3 ou 4 axes ? conserver le maximum de l'information.
Les Vecteurs propres des variables
Les vecteurs propres sont les coefficients ? affecter aux variables initiales pour obtenir les composantes principales. Pour une variable donn?e, il existe un lien entre la corr?lation et le vecteur propre suivant une composante donn?e: Vecteurs propres = corr?lation_avec_axe/Sdev_axe.
| NOM | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 | Comp6 |
|---|---|---|---|---|---|---|
| VAR1 | -0.425 | 0.124 | -0.354 | 0.808 | -0.152 | -0.059 |
| VAR2 | -0.422 | 0.416 | -0.185 | -0.358 | 0.294 | -0.633 |
| VAR3 | -0.421 | -0.412 | 0.068 | -0.28 | -0.731 | -0.19 |
| VAR4 | -0.387 | -0.446 | 0.605 | 0.212 | 0.478 | -0.11 |
| VAR5 | -0.431 | -0.243 | -0.484 | -0.302 | 0.305 | 0.581 |
| VAR6 | -0.359 | 0.62 | 0.485 | -0.074 | -0.189 | 0.459 |
Pour chaque individu la pr?mi?re composante principale s'obtient par exemple avec la formule : (-0.425*VAR1)+(-0.422*VAR2)+....+....(0.359*VAR6).
Exemples
Tableau de donn?es
| Modele | VAR1 | VAR2 | VAR3 | VAR4 | VAR5 | VAR6 |
|---|---|---|---|---|---|---|
| IND1 | 1350 | 79 | 393 | 161 | 870 | 165 |
| IND2 | 1588 | 85 | 468 | 177 | 1110 | 160 |
| IND3 | 1294 | 68 | 424 | 168 | 1050 | 152 |
| IND4 | 1222 | 59 | 412 | 161 | 930 | 151 |
| IND5 | 1585 | 98 | 439 | 164 | 1105 | 165 |
| IND6 | 1297 | 82 | 429 | 169 | 1080 | 160 |
| IND7 | 1796 | 79 | 449 | 169 | 1160 | 154 |
| IND8 | 1565 | 55 | 424 | 163 | 1010 | 140 |
| IND9 | 2664 | 128 | 452 | 173 | 1320 | 180 |
| IND10 | 1166 | 55 | 399 | 157 | 815 | 140 |
| IND11 | 1570 | 109 | 428 | 162 | 1060 | 175 |
| IND12 | 1798 | 82 | 445 | 172 | 1160 | 158 |
| IND13 | 1998 | 115 | 469 | 169 | 1370 | 160 |
| IND14 | 1993 | 98 | 438 | 170 | 1080 | 167 |
| IND15 | 1442 | 80 | 431 | 166 | 1129 | 144 |
| IND16 | 1769 | 83 | 440 | 165 | 1095 | 165 |
| IND17 | 1979 | 100 | 459 | 173 | 1120 | 173 |
| IND18 | 1294 | 68 | 404 | 161 | 955 | 140 |
Le tableau contient 18 individus avec 6 variables d?crivant les individus.
Nuage de points : R?lation entre les variables
Chaque variable est repr?sent?e en fonction des
autre
variables permettant de voir la r?lation entre les variables
2
par 2.

Valeurs propres - Variances - pourcentage d'inertie de chaque composante
Tableau des valeurs propres
| NOM | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 | Comp6 |
|---|---|---|---|---|---|---|
| Variance | 4.42 | 0.86 | 0.37 | 0.21 | 0.09 | 0.04 |
| % de Variance | 73.68 | 14.27 | 6.22 | 3.57 | 1.55 | 0.72 |
| % de Variance cumul?e | 73.68 | 87.95 | 94.17 | 97.73 | 99.28 | 100 |
Graphiques des valeurs propres
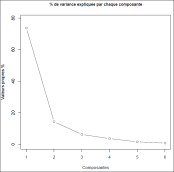
|
Le tableau ci-dessus et la figure ci-contre , montre qu'uniquement avec les composantes 1 et 2 on a 88% de l'information. Avec cette analyse on peut s'en tenir aux 2 premiers axes |
Plan des variables
Le cercle de corr?lation
Les variables sont projet?es dans un cercle de rayon 1
appel? cercle des corr?lations. Lorsqu'une
variable est
proche du bord du cercle, on dit qu'il est bien
repr?sent? par le plan factoriel. Cette variable
est
alors bien correl?e avec les 2 facteurs principaux
constituant
ce plan.
Le cercle permet de voir la corr?lation ou la liaison entre
les variables.
La corr?lation entre 2 points variables est ?gale
au
cosinus de l'angle entre les 2 variables. Plus cet angle est petit plus
la corr?lation est forte.
- Si l'angle = 90? => Cos
= 0 => pas de corr?lation
- Si l'angle = 180? => Cos = -1
=> Corr?lation inverse forte entre les 2 variables.

Le cercle des corr?lations permet de voir, parmi les
anciennes variables, les groupes de variables tr?s
corr?l?es entre elles.
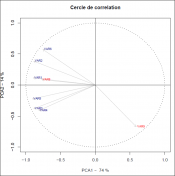
Remarque :
Dans le cercle ci-dessus, toutes les variables sont bien
repr?sent?es par le plan. On note une
tr?s forte
corr?lation entre la variable 3 et 4.
Coordonn?es des variables - Coefficient de corr?lation des variables avec les diff?rentes composantes
| NAME | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 | Comp6 |
|---|---|---|---|---|---|---|
| VAR1 | -0,89 | 0,11 | -0,22 | 0,37 | -0,05 | -0,01 |
| VAR2 | -0,89 | 0,38 | -0,11 | -0,17 | 0,09 | -0,13 |
| VAR3 | -0,89 | -0,38 | 0,04 | -0,13 | -0,22 | -0,04 |
| VAR4 | -0,81 | -0,41 | 0,37 | 0,10 | 0,15 | -0,02 |
| VAR5 | -0,91 | -0,22 | -0,30 | -0,14 | 0,09 | 0,12 |
| VAR6 | -0,75 | 0,57 | 0,30 | -0,03 | -0,06 | 0,10 |
Qualit? de la repr?sentation des variables par l'ACP - Corr?lation au carr? = COS^2
La qualit? de la repr?sentation d'une variable selon un axe principal est donn? par le carr? de son coefficient de corr?lation avec cet axe et repr?sente le cosinus carr?. COS2 = COR*COR
| NOM | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 | Comp6 |
|---|---|---|---|---|---|---|
| VAR1 | 0.8 | 0.01 | 0.05 | 0.14 | 0 | 0 |
| VAR2 | 0.79 | 0.15 | 0.01 | 0.03 | 0.01 | 0.02 |
| VAR3 | 0.79 | 0.15 | 0 | 0.02 | 0.05 | 0 |
| VAR4 | 0.66 | 0.17 | 0.14 | 0.01 | 0.02 | 0 |
| VAR5 | 0.82 | 0.05 | 0.09 | 0.02 | 0.01 | 0.01 |
| VAR6 | 0.57 | 0.33 | 0.09 | 0 | 0 | 0.01 |
Pour chaque variable la somme horizontale(lorsque l'on prend toutes les composantes) est ?gale ? 1 (100%) La variable VAR1 est repr?sent?e ? 80% par la composante 1. La qualit? de la repr?sentation d'une variable sur les axes selectionn?s est la somme des COS2 des axes. Par exemple la La qualit? de la repr?sentation de la variable VAR2 par le plan form? par les composantes 1 et 2 = 0.79+0.15=0.94
Poids d'une variable dans la definition d'une composante principale
C'est la part en % du COS2 de la variable. Par exemple le poids de la variable VAR1 dans la d?finition de la composante 1 est : 0.8*100/(0.8+0.79+0.79+0.66+0.82+0.57) = 18%.
| NOM | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 | Comp6 |
|---|---|---|---|---|---|---|
| VAR1 | 18.057 | 1.542 | 12.504 | 65.252 | 2.298 | 0.347 |
| VAR2 | 17.791 | 17.287 | 3.42 | 12.802 | 8.628 | 40.073 |
| VAR3 | 17.763 | 16.959 | 0.457 | 7.826 | 53.373 | 3.621 |
| VAR4 | 14.971 | 19.899 | 36.587 | 4.476 | 22.867 | 1.2 |
| VAR5 | 18.534 | 5.889 | 23.464 | 9.103 | 9.276 | 33.734 |
| VAR6 | 12.884 | 38.423 | 23.568 | 0.541 | 3.559 | 21.024 |
La somme verticale =100% Le poids de la variable 1 dans la definition de la composante est de 18% alors qu'elle n'est que de 1.5% pour la definition de la composante 2.
Plan des individus
Repr?sentation des individus sur les 2 pr?miers axes
Repr?sentation simultan?e des individus et des variables
Coordonn?es des individus dans le plan factoriel
| NAME | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 | Comp6 |
|---|---|---|---|---|---|---|
| IND1 | 2.14 | 1.79 | 0.572 | 0.202 | 0.301 | 0.0539 |
| IND2 | -1.56 | -1.53 | 1.32 | -0.211 | -0.149 | -0.327 |
| IND3 | 1.12 | -0.675 | 0.457 | -0.168 | 0.375 | 0.272 |
| IND4 | 2.57 | 0.113 | 0.149 | -0.0173 | -0.227 | 0.263 |
| IND5 | -0.428 | 0.696 | -0.193 | -0.628 | -0.264 | -0.0372 |
| IND6 | 0.304 | -0.196 | 0.676 | -0.556 | 0.445 | 0.2 |
| IND7 | -0.684 | -0.933 | -0.257 | 0.203 | -0.209 | 0.154 |
| IND8 | 1.95 | -0.98 | -0.62 | 0.63 | -0.293 | 0.109 |
| IND9 | -4.41 | 1.06 | -0.594 | 0.847 | 0.375 | 0.044 |
| IND10 | 3.99 | 0.236 | -0.303 | 0.265 | -0.278 | -0.329 |
| IND11 | -0.438 | 1.91 | 0.0249 | -0.759 | -0.168 | -0.0542 |
| IND12 | -1.02 | -0.842 | 0.217 | 0.303 | 0.185 | 0.185 |
| IND13 | -2.94 | -0.559 | -1.24 | -0.772 | -0.0544 | -0.0573 |
| IND14 | -1.31 | 0.487 | 0.283 | 0.582 | 0.0667 | -0.253 |
| IND15 | 0.691 | -0.898 | -0.628 | -0.358 | 0.377 | -0.122 |
| IND16 | -0.386 | 0.356 | -0.0756 | 0.103 | -0.527 | 0.339 |
| IND17 | -2.29 | 0.104 | 0.796 | 0.236 | -0.338 | -0.157 |
| IND18 | 2.71 | -0.144 | -0.574 | 0.0962 | 0.382 | -0.283 |
Qualit? de la repr?sentation des individus en % selon les composantes principales - COS2
La qualit? de la repr?sentation d'un individu par un axe U est donn?e par le carr? de la distance de l'individu au centre de gravit?. La qualit? de la repr?sentation d'un point M par un plan factoriel constitu? de 2 axes est mesur?e par la somme des cos2 avec 2 axes .
| NAME | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 | Comp6 |
|---|---|---|---|---|---|---|
| IND1 | 55.622 | 38.767 | 3.976 | 0.496 | 1.104 | 0.035 |
| IND2 | 36.533 | 34.941 | 25.922 | 0.669 | 0.331 | 1.605 |
| IND3 | 58.028 | 21.069 | 9.655 | 1.301 | 6.525 | 3.421 |
| IND4 | 97.699 | 0.188 | 0.326 | 0.004 | 0.759 | 1.024 |
| IND5 | 15.658 | 41.383 | 3.195 | 33.707 | 5.939 | 0.118 |
| IND6 | 8.155 | 3.39 | 40.241 | 27.232 | 17.455 | 3.527 |
| IND7 | 30.92 | 57.549 | 4.36 | 2.728 | 2.878 | 1.565 |
| IND8 | 67.354 | 17.054 | 6.81 | 7.048 | 1.525 | 0.209 |
| IND9 | 89.243 | 5.192 | 1.617 | 3.294 | 0.645 | 0.009 |
| IND10 | 97.522 | 0.343 | 0.564 | 0.431 | 0.476 | 0.664 |
| IND11 | 4.298 | 82.065 | 0.014 | 12.923 | 0.634 | 0.066 |
| IND12 | 53.095 | 36.286 | 2.403 | 4.715 | 1.751 | 1.751 |
| IND13 | 77.839 | 2.814 | 13.926 | 5.366 | 0.027 | 0.03 |
| IND14 | 70.482 | 9.65 | 3.256 | 13.819 | 0.182 | 2.611 |
| IND15 | 24.327 | 41.047 | 20.113 | 6.518 | 7.242 | 0.752 |
| IND16 | 21.734 | 18.534 | 0.835 | 1.547 | 40.579 | 16.772 |
| IND17 | 86.19 | 0.179 | 10.426 | 0.918 | 1.883 | 0.404 |
| IND18 | 92.605 | 0.261 | 4.164 | 0.117 | 1.84 | 1.014 |
La somme horizontale = 100%
Calcul du cosinus carr?
- Calculer la moyenne et l'?cart type de chaque variable
- distance de l'individu i au centre
d = (VAR1INDi-MoyVAR1)/SDVAR1 + (VAR2INDi-MoyVAR2)/SDVAR2
+ ??.+ (VARNINDi-MoyVARN)/SDVARN
Contribution des individus aux composantes en %
| NAME | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 | Comp6 |
|---|---|---|---|---|---|---|
| IND1 | 5.749 | 20.693 | 4.87 | 1.059 | 5.437 | 0.373 |
| IND2 | 3.064 | 15.133 | 25.762 | 1.16 | 1.32 | 13.743 |
| IND3 | 1.575 | 2.953 | 3.104 | 0.73 | 8.435 | 9.481 |
| IND4 | 8.324 | 0.083 | 0.329 | 0.008 | 3.081 | 8.909 |
| IND5 | 0.23 | 3.14 | 0.556 | 10.234 | 4.157 | 0.177 |
| IND6 | 0.116 | 0.25 | 6.801 | 8.027 | 11.859 | 5.138 |
| IND7 | 0.588 | 5.65 | 0.982 | 1.072 | 2.606 | 3.039 |
| IND8 | 4.771 | 6.238 | 5.716 | 10.318 | 5.145 | 1.515 |
| IND9 | 24.437 | 7.342 | 5.246 | 18.642 | 8.414 | 0.248 |
| IND10 | 19.964 | 0.362 | 1.368 | 1.825 | 4.641 | 13.882 |
| IND11 | 0.241 | 23.736 | 0.009 | 14.957 | 1.692 | 0.378 |
| IND12 | 1.303 | 4.598 | 0.699 | 2.391 | 2.046 | 4.387 |
| IND13 | 10.87 | 2.029 | 23.045 | 15.485 | 0.177 | 0.421 |
| IND14 | 2.173 | 1.536 | 1.189 | 8.804 | 0.267 | 8.22 |
| IND15 | 0.6 | 5.23 | 5.881 | 3.324 | 8.512 | 1.895 |
| IND16 | 0.187 | 0.823 | 0.085 | 0.275 | 16.629 | 14.733 |
| IND17 | 6.589 | 0.071 | 9.445 | 1.451 | 6.858 | 3.15 |
| IND18 | 9.219 | 0.134 | 4.912 | 0.24 | 8.724 | 10.311 |
Cet tableau permet de determiner les individus qui p?se le plus dans la definition d'une composante.
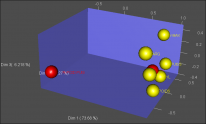
Repr?sentation 3D
Ellipse 3d de concentration des donn?es
Les individus supplementaires ou illustratifs ou inactifs : Positionner des individus n?ayant pas particip? ? la construction des axes
| NOM | VAR1 | VAR2 | VAR3 | VAR4 | VAR5 | VAR6 |
|---|---|---|---|---|---|---|
| INDX | 2664 | 136 | 472 | 177 | 1410 | 180 |
| INDY | 1288 | 74 | 414 | 157 | 915 | 160 |
On peut mettre en supplementaire des individus dont la position est ? pr?dire ou des individus dont on doute de la fiabilit?. Les individus qui ont particip? ? la construction des axes (individus non supplementaires) sont dits actifs. Les individus suppl?mentaires sont introduits en fin d?analyse, apr?s le calcul des vecteurs propres. Le calcul des coordonn?es des individus suppl?mentaire se fait en utilisant les vecteurs propres des variables d?j? connus de l'ACP.
M?thode de calcul des coordonn?es des individus suppl?mentaires
- Moyenne et ?cart type de l'ACP (Moyenne et ?cart type des variables d?j? connus) - centrage et r?duction des variables pour chaque individu en utilisant les moyennes et ?carts-type de l'ACP - calcul des coordonn?es factorielles suivant les axes (en utilisant les vecteurs propres de l'acp) - Pour chaque individu la pr?mi?re composante principale s'obtient par exemple avec la formule: (-0.425*VAR1)+(-0.422*VAR2)+....+....(0.359*VAR6). - Pour obtenir les coordonn?es suivant la 2?me composante, il faudra utiliser les vecteurs propres des variables suivant la 2?me composante ....Ainsi de suite....... Les variables sont remplac?es par les valeurs centr?es et r?duites.
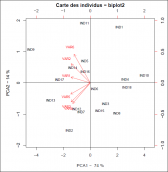
Graphique des individus suppl?mentaires
Les individus suppl?mentaires sont en rouge.
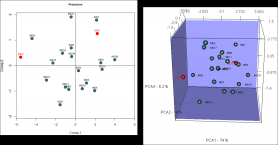
Coordonn?es des individus suppl?mentaires
| NOM | Comp1 | Comp2 | Comp3 | Comp4 | Comp5 | Comp6 |
|---|---|---|---|---|---|---|
| INDX | -5.563 | 0.339 | -0.464 | 0.402 | 0.39 | -0.081 |
| INDY | 2.212 | 1.258 | -0.093 | -0.354 | -0.649 | 0.125 |
Les variables suppl?mentaires ou illustratifs
On peut mettre des variables ? expliquer en suppl?mentaire. Par opposition les variables explicatives seront utilis?es pour faire l'ACP. La variables ? expliquer est introduite ? la fin de l'analyse afin de la positionner sur le plan principal. D'autres variables peuvent manquer de fiabilit?. On peut h?siter ? les introduire dans l'analyse. Elles peuvent ?tre utilis?es comme variables suppl?mentaires. Les variables suppl?mentaires peuvent ?tre soient qualitatives soit quantitatives
Variables quantitatives illustratives : Positionnement dans le cercle des corr?lations
M?thodes:Determiner la corr?lation entre chaque variable quantitatives et les composantes (1 et 2 par exemple) puis positionner sur le cercle de corr?lation.
Variables qualitatives illustratives : Positionner les groupes des variables
Calcul de la moyenne de chaque groupe suivant les composantes
|
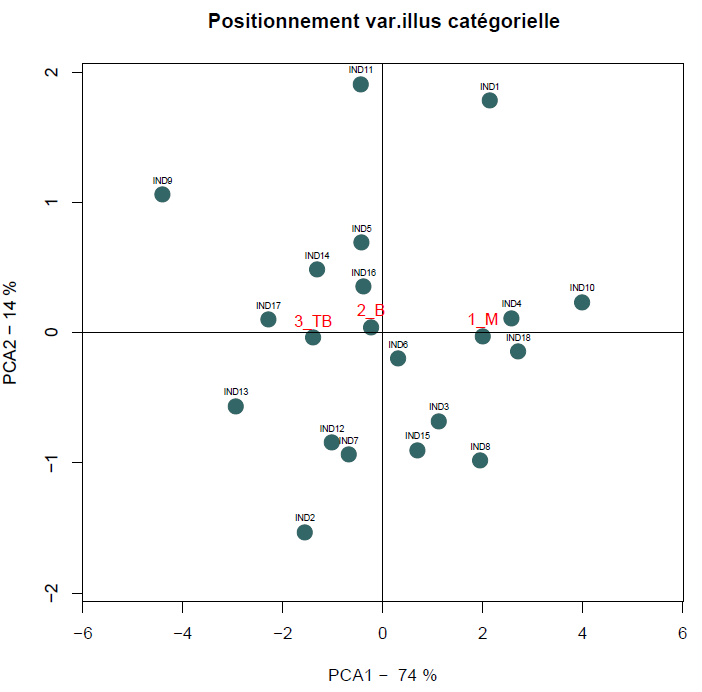 |
Les individus se diff?rencient v?ritablement par leur groupe suivant la premi?re composante
Repr?sentation des individus dans le plan en fonction de leur groupe
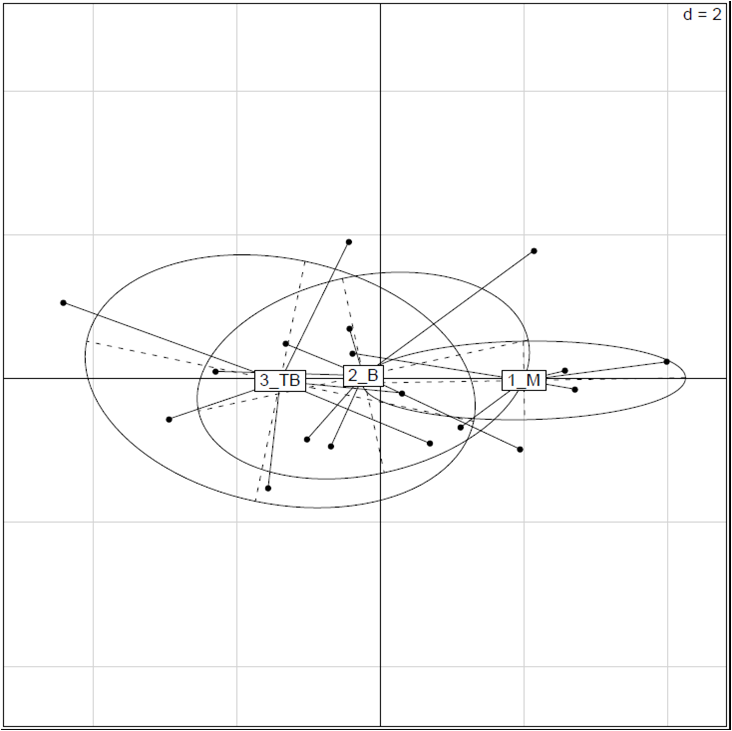
R?f?rences
- Cour L3 (Maryse Raffestin ? octobre 2005)
- Andr? Bouchier (Formation INRA 2006)
- Ali Kouani