The classification of observations into groups requires some methods for computing the distance or the (dis)similarity between each pair of observations. The result of this computation is known as a dissimilarity or distance matrix.
There are many methods to calculate this distance information. In this article, we describe the common distance measures and provide R codes for computing and visualizing distances.
Contents:
Related Book
Practical Guide to Cluster Analysis in RMethods for measuring distances
The choice of distance measures is a critical step in clustering. It defines how the similarity of two elements (x, y) is calculated and it will influence the shape of the clusters.
The classical methods for distance measures are Euclidean and Manhattan distances, which are defined as follow:
- Euclidean distance:
\[
d_{euc}(x,y) = \sqrt{\sum_{i=1}^n(x_i - y_i)^2}
\]
- Manhattan distance:
\[
d_{man}(x,y) = \sum_{i=1}^n |{(x_i - y_i)|}
\]
Where, x and y are two vectors of length n.
Other dissimilarity measures exist such as correlation-based distances, which is widely used for gene expression data analyses. Correlation-based distance is defined by subtracting the correlation coefficient from 1. Different types of correlation methods can be used such as:
- Pearson correlation distance:
\[
d_{cor}(x, y) = 1 - \frac{\sum\limits_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum\limits_{i=1}^n(x_i - \bar{x})^2 \sum\limits_{i=1}^n(y_i -\bar{y})^2}}
\]
Pearson correlation measures the degree of a linear relationship between two profiles.
- Eisen cosine correlation distance (Eisen et al., 1998):
It’s a special case of Pearson’s correlation with \(\bar{x}\) and \(\bar{y}\) both replaced by zero:
\[
d_{eisen}(x, y) = 1 - \frac{\left|\sum\limits_{i=1}^n x_iy_i\right|}{\sqrt{\sum\limits_{i=1}^n x^2_i \sum\limits_{i=1}^n y^2_i}}
\]
- Spearman correlation distance:
The spearman correlation method computes the correlation between the rank of x and the rank of y variables.
\[
d_{spear}(x, y) = 1 - \frac{\sum\limits_{i=1}^n (x'_i - \bar{x'})(y'_i - \bar{y'})}{\sqrt{\sum\limits_{i=1}^n(x'_i - \bar{x'})^2 \sum\limits_{i=1}^n(y'_i -\bar{y'})^2}}
\]
Where \(x'_i = rank(x_i)\) and \(y'_i = rank(y)\).
- Kendall correlation distance:
Kendall correlation method measures the correspondence between the ranking of x and y variables. The total number of possible pairings of x with y observations is \(n(n-1)/2\), where n is the size of x and y. Begin by ordering the pairs by the x values. If x and y are correlated, then they would have the same relative rank orders. Now, for each \(y_i\), count the number of \(y_j > y_i\) (concordant pairs (c)) and the number of \(y_j < y_i\) (discordant pairs (d)).
Kendall correlation distance is defined as follow:
\[
d_{kend}(x, y) = 1 - \frac{n_c - n_d}{\frac{1}{2}n(n-1)}
\]
Where,
- \(n_c\): total number of concordant pairs
- \(n_d\): total number of discordant pairs
- \(n\): size of x and y
Note that,
- Pearson correlation analysis is the most commonly used method. It is also known as a parametric correlation which depends on the distribution of the data.
- Kendall and Spearman correlations are non-parametric and they are used to perform rank-based correlation analysis.
In the formula above, x and y are two vectors of length n and, means \(\bar{x}\) and \(\bar{y}\), respectively. The distance between x and y is denoted d(x, y).
What type of distance measures should we choose?
The choice of distance measures is very important, as it has a strong influence on the clustering results. For most common clustering software, the default distance measure is the Euclidean distance.
Depending on the type of the data and the researcher questions, other dissimilarity measures might be preferred. For example, correlation-based distance is often used in gene expression data analysis.
Correlation-based distance considers two objects to be similar if their features are highly correlated, even though the observed values may be far apart in terms of Euclidean distance. The distance between two objects is 0 when they are perfectly correlated. Pearson’s correlation is quite sensitive to outliers. This does not matter when clustering samples, because the correlation is over thousands of genes. When clustering genes, it is important to be aware of the possible impact of outliers. This can be mitigated by using Spearman’s correlation instead of Pearson’s correlation.
If we want to identify clusters of observations with the same overall profiles regardless of their magnitudes, then we should go with correlation-based distance as a dissimilarity measure. This is particularly the case in gene expression data analysis, where we might want to consider genes similar when they are “up” and “down” together. It is also the case, in marketing if we want to identify group of shoppers with the same preference in term of items, regardless of the volume of items they bought.
If Euclidean distance is chosen, then observations with high values of features will be clustered together. The same holds true for observations with low values of features.
Data standardization
The value of distance measures is intimately related to the scale on which measurements are made. Therefore, variables are often scaled (i.e. standardized) before measuring the inter-observation dissimilarities. This is particularly recommended when variables are measured in different scales (e.g: kilograms, kilometers, centimeters, …); otherwise, the dissimilarity measures obtained will be severely affected.
The goal is to make the variables comparable. Generally variables are scaled to have i) standard deviation one and ii) mean zero.
The standardization of data is an approach widely used in the context of gene expression data analysis before clustering. We might also want to scale the data when the mean and/or the standard deviation of variables are largely different.
When scaling variables, the data can be transformed as follow:
\[
\frac{x_i - center(x)}{scale(x)}
\]
Where \(center(x)\) can be the mean or the median of x values, and \(scale(x)\) can be the standard deviation (SD), the interquartile range, or the MAD (median absolute deviation).
The R base function scale() can be used to standardize the data. It takes a numeric matrix as an input and performs the scaling on the columns.
Standardization makes the four distance measure methods - Euclidean, Manhattan, Correlation and Eisen - more similar than they would be with non-transformed data.
Note that, when the data are standardized, there is a functional relationship between the Pearson correlation coefficient r(x, y) and the Euclidean distance.
With some maths, the relationship can be defined as follow:
\[
d_{euc}(x, y) = \sqrt{2m[1 - r(x, y)]}
\]
Where x and y are two standardized m-vectors with zero mean and unit length.
Therefore, the result obtained with Pearson correlation measures and standardized Euclidean distances are comparable.
Distance matrix computation
Data preparation
We’ll use the USArrests data as demo data sets. We’ll use only a subset of the data by taking 15 random rows among the 50 rows in the data set. This is done by using the function sample(). Next, we standardize the data using the function scale():
# Subset of the data
set.seed(123)
ss <- sample(1:50, 15) # Take 15 random rows
df <- USArrests[ss, ] # Subset the 15 rows
df.scaled <- scale(df) # Standardize the variablesR functions and packages
There are many R functions for computing distances between pairs of observations:
- dist() R base function [stats package]: Accepts only numeric data as an input.
- get_dist() function [factoextra package]: Accepts only numeric data as an input. Compared to the standard dist() function, it supports correlation-based distance measures including “pearson”, “kendall” and “spearman” methods.
- daisy() function [cluster package]: Able to handle other variable types (e.g. nominal, ordinal, (a)symmetric binary). In that case, the Gower’s coefficient will be automatically used as the metric. It’s one of the most popular measures of proximity for mixed data types. For more details, read the R documentation of the daisy() function (?daisy).
All these functions compute distances between rows of the data.
Computing euclidean distance
To compute Euclidean distance, you can use the R base dist() function, as follow:
dist.eucl <- dist(df.scaled, method = "euclidean")Note that, allowed values for the option method include one of: “euclidean”, “maximum”, “manhattan”, “canberra”, “binary”, “minkowski”.
To make it easier to see the distance information generated by the dist() function, you can reformat the distance vector into a matrix using the as.matrix() function.
# Reformat as a matrix
# Subset the first 3 columns and rows and Round the values
round(as.matrix(dist.eucl)[1:3, 1:3], 1)## Iowa Rhode Island Maryland
## Iowa 0.0 2.8 4.1
## Rhode Island 2.8 0.0 3.6
## Maryland 4.1 3.6 0.0In this matrix, the value represent the distance between objects. The values on the diagonal of the matrix represent the distance between objects and themselves (which are zero).
In this data set, the columns are variables. Hence, if we want to compute pairwise distances between variables, we must start by transposing the data to have variables in the rows of the data set before using the dist() function. The function t() is used for transposing the data.
Computing correlation based distances
Correlation-based distances are commonly used in gene expression data analysis.
The function get_dist()[factoextra package] can be used to compute correlation-based distances. Correlation method can be either pearson, spearman or kendall.
# Compute
library("factoextra")
dist.cor <- get_dist(df.scaled, method = "pearson")
# Display a subset
round(as.matrix(dist.cor)[1:3, 1:3], 1)## Iowa Rhode Island Maryland
## Iowa 0.0 0.4 1.9
## Rhode Island 0.4 0.0 1.5
## Maryland 1.9 1.5 0.0Computing distances for mixed data
The function daisy() [cluster package] provides a solution (Gower’s metric) for computing the distance matrix, in the situation where the data contain no-numeric columns.
The R code below applies the daisy() function on flower data which contains factor, ordered and numeric variables:
library(cluster)
# Load data
data(flower)
head(flower, 3)## V1 V2 V3 V4 V5 V6 V7 V8
## 1 0 1 1 4 3 15 25 15
## 2 1 0 0 2 1 3 150 50
## 3 0 1 0 3 3 1 150 50# Data structure
str(flower)## 'data.frame': 18 obs. of 8 variables:
## $ V1: Factor w/ 2 levels "0","1": 1 2 1 1 1 1 1 1 2 2 ...
## $ V2: Factor w/ 2 levels "0","1": 2 1 2 1 2 2 1 1 2 2 ...
## $ V3: Factor w/ 2 levels "0","1": 2 1 1 2 1 1 1 2 1 1 ...
## $ V4: Factor w/ 5 levels "1","2","3","4",..: 4 2 3 4 5 4 4 2 3 5 ...
## $ V5: Ord.factor w/ 3 levels "1"<"2"<"3": 3 1 3 2 2 3 3 2 1 2 ...
## $ V6: Ord.factor w/ 18 levels "1"<"2"<"3"<"4"<..: 15 3 1 16 2 12 13 7 4 14 ...
## $ V7: num 25 150 150 125 20 50 40 100 25 100 ...
## $ V8: num 15 50 50 50 15 40 20 15 15 60 ...# Distance matrix
dd <- daisy(flower)
round(as.matrix(dd)[1:3, 1:3], 2)## 1 2 3
## 1 0.00 0.89 0.53
## 2 0.89 0.00 0.51
## 3 0.53 0.51 0.00Visualizing distance matrices
A simple solution for visualizing the distance matrices is to use the function fviz_dist() [factoextra package]. Other specialized methods, such as agglomerative hierarchical clustering or heatmap will be comprehensively described in the dedicated courses.
To use fviz_dist() type this:
library(factoextra)
fviz_dist(dist.eucl)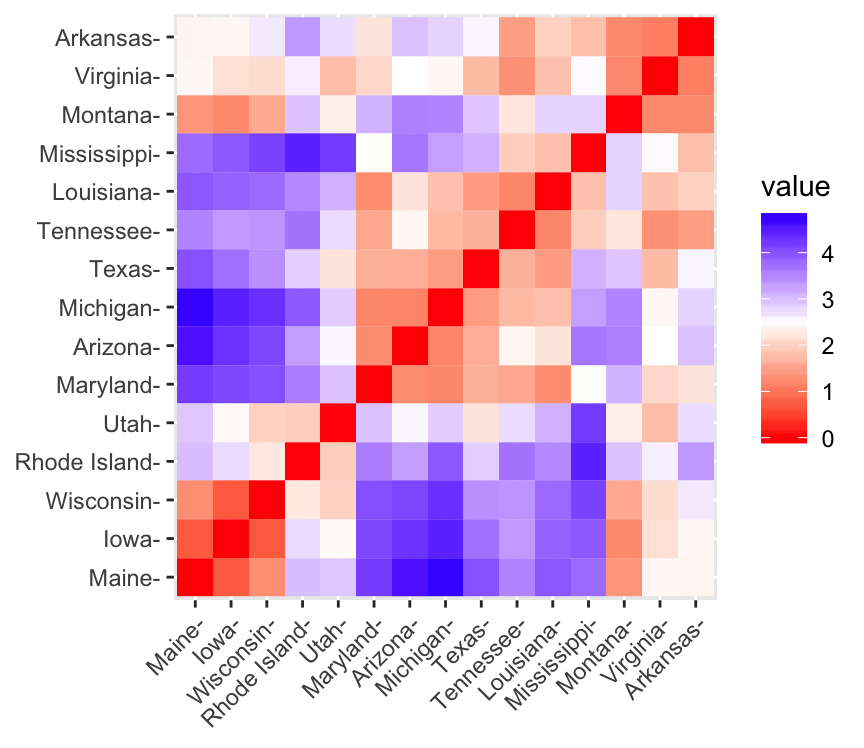
- Red: high similarity (ie: low dissimilarity) | Blue: low similarity
The color level is proportional to the value of the dissimilarity between observations: pure red if \(dist(x_i, x_j) = 0\) and pure blue corresponds to the highest value of euclidean distance computed. Objects belonging to the same cluster are displayed in consecutive order.
Summary
We described how to compute distance matrices using either Euclidean or correlation-based measures. It’s generally recommended to standardize the variables before distance matrix computation. Standardization makes variable comparable, in the situation where they are measured in different scales.
Recommended for you
This section contains best data science and self-development resources to help you on your path.
Coursera - Online Courses and Specialization
Data science
- Course: Machine Learning: Master the Fundamentals by Stanford
- Specialization: Data Science by Johns Hopkins University
- Specialization: Python for Everybody by University of Michigan
- Courses: Build Skills for a Top Job in any Industry by Coursera
- Specialization: Master Machine Learning Fundamentals by University of Washington
- Specialization: Statistics with R by Duke University
- Specialization: Software Development in R by Johns Hopkins University
- Specialization: Genomic Data Science by Johns Hopkins University
Popular Courses Launched in 2020
- Google IT Automation with Python by Google
- AI for Medicine by deeplearning.ai
- Epidemiology in Public Health Practice by Johns Hopkins University
- AWS Fundamentals by Amazon Web Services
Trending Courses
- The Science of Well-Being by Yale University
- Google IT Support Professional by Google
- Python for Everybody by University of Michigan
- IBM Data Science Professional Certificate by IBM
- Business Foundations by University of Pennsylvania
- Introduction to Psychology by Yale University
- Excel Skills for Business by Macquarie University
- Psychological First Aid by Johns Hopkins University
- Graphic Design by Cal Arts
Amazon FBA
Amazing Selling Machine
Books - Data Science
Our Books
- Practical Guide to Cluster Analysis in R by A. Kassambara (Datanovia)
- Practical Guide To Principal Component Methods in R by A. Kassambara (Datanovia)
- Machine Learning Essentials: Practical Guide in R by A. Kassambara (Datanovia)
- R Graphics Essentials for Great Data Visualization by A. Kassambara (Datanovia)
- GGPlot2 Essentials for Great Data Visualization in R by A. Kassambara (Datanovia)
- Network Analysis and Visualization in R by A. Kassambara (Datanovia)
- Practical Statistics in R for Comparing Groups: Numerical Variables by A. Kassambara (Datanovia)
- Inter-Rater Reliability Essentials: Practical Guide in R by A. Kassambara (Datanovia)
Others
- R for Data Science: Import, Tidy, Transform, Visualize, and Model Data by Hadley Wickham & Garrett Grolemund
- Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems by Aurelien Géron
- Practical Statistics for Data Scientists: 50 Essential Concepts by Peter Bruce & Andrew Bruce
- Hands-On Programming with R: Write Your Own Functions And Simulations by Garrett Grolemund & Hadley Wickham
- An Introduction to Statistical Learning: with Applications in R by Gareth James et al.
- Deep Learning with R by François Chollet & J.J. Allaire
- Deep Learning with Python by François Chollet



Hi, can you do a tutorial how to make a mathematical equations using mathjaxr just like you made above? I really interested. Thank you.
I actually found the solution! Oh my God! It took me like 3 hours to surfing from one blog to another just to find the solution. I’ve encountered some using Rd file, Mathjaxr, etc.
And the solution is you just need to put two dollar sign $$ as the opening and closing delimiter or bracket (?) to act as wrapper around the equation.
Here’s the link I finally found. Covered pretty much everything you needed to create nice mathematical equations.
https://rpruim.github.io/s341/S19/from-class/MathinRmd.html
You could also use this \[ as opening, and \] as closing bracket.
\[mean(x)\]
Correction.
Use`\[` as opening, and `\]` as closing bracket
Example: `\[\frac{x_i – center(x)}{scale(x)}\]`
Will produce this: \[\frac{x_i – center(x)}{scale(x)}\]