Clustering methods are used to identify groups of similar objects in a multivariate data sets collected from fields such as marketing, bio-medical and geo-spatial. They are different types of clustering methods, including:
- Partitioning methods
- Hierarchical clustering
- Fuzzy clustering
- Density-based clustering
- Model-based clustering
In this article, we provide an overview of clustering methods and quick start R code to perform cluster analysis in R:
- we start by presenting required R packages and data format for cluster analysis and visualization.
- next, we describe the two standard clustering techniques [partitioning methods (k-MEANS, PAM, CLARA) and hierarchical clustering] as well as how to assess the quality of clustering analysis.
- finally, we describe advanced clustering approaches to find pattern of any shape in large data sets with noise and outliers.
Contents:
Contents:
Related Book
Practical Guide to Cluster Analysis in RInstalling and loading required R packages
We’ll use mainly two R packages:
- cluster package: for computing clustering
- factoextra package : for elegant ggplot2-based data visualization. Online documentation at: https://rpkgs.datanovia.com/factoextra/
Accessory packages:
- magrittr for piping: %>%
Install:
install.packages("factoextra")
install.packages("cluster")
install.packages("magrittr")Load packages:
library("cluster")
library("factoextra")
library("magrittr")Data preparation
- Demo data set: the built-in R dataset named USArrest
- Remove missing data
- Scale variables to make them comparable
Read more: Data Preparation and Essential R Packages for Cluster Analysis
# Load and prepare the data
data("USArrests")
my_data <- USArrests %>%
na.omit() %>% # Remove missing values (NA)
scale() # Scale variables
# View the firt 3 rows
head(my_data, n = 3)## Murder Assault UrbanPop Rape
## Alabama 1.2426 0.783 -0.521 -0.00342
## Alaska 0.5079 1.107 -1.212 2.48420
## Arizona 0.0716 1.479 0.999 1.04288Distance measures
The classification of objects, into clusters, requires some methods for measuring the distance or the (dis)similarity between the objects. Chapter Clustering Distance Measures Essentials covers the common distance measures used for assessing similarity between observations.
It’s simple to compute and visualize distance matrix using the functions get_dist() and fviz_dist() [factoextra R package]:
get_dist(): for computing a distance matrix between the rows of a data matrix. Compared to the standarddist()function, it supports correlation-based distance measures including “pearson”, “kendall” and “spearman” methods.fviz_dist(): for visualizing a distance matrix
res.dist <- get_dist(USArrests, stand = TRUE, method = "pearson")
fviz_dist(res.dist,
gradient = list(low = "#00AFBB", mid = "white", high = "#FC4E07"))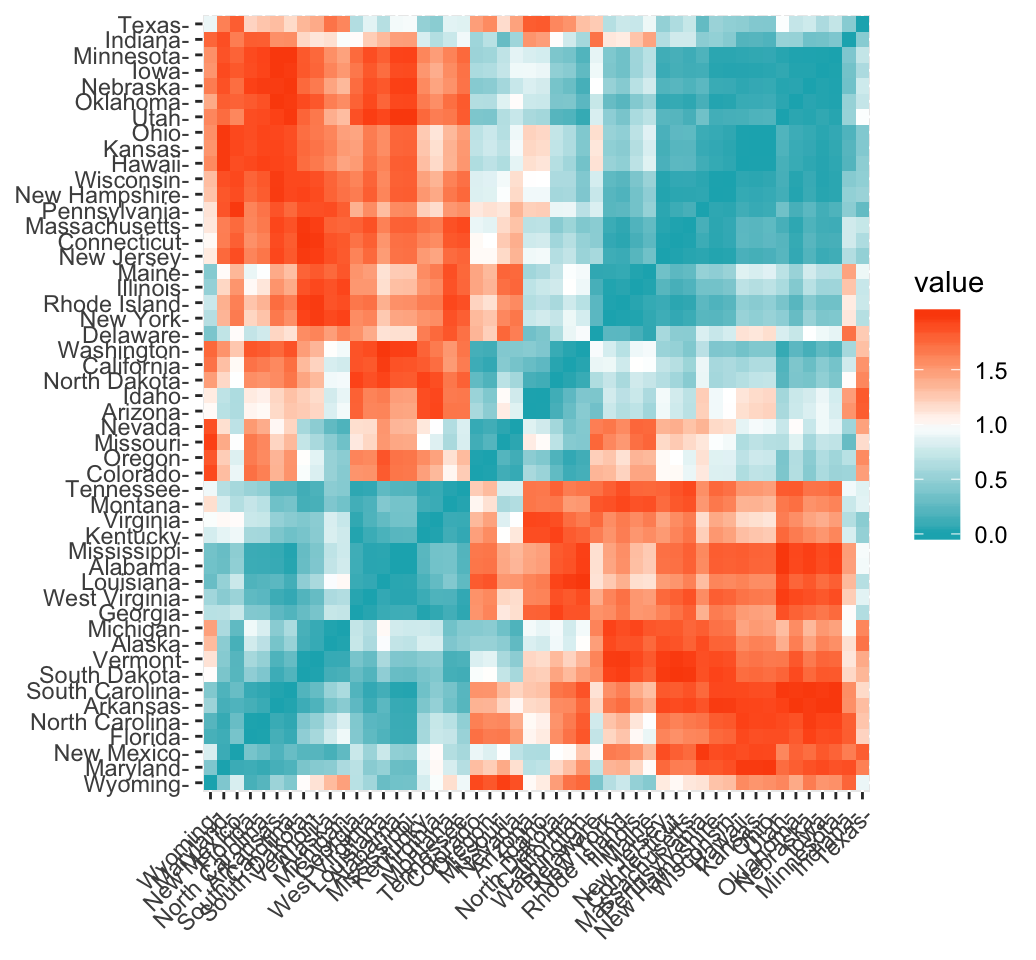
Read more: Clustering Distance Measures Essentials
Partitioning clustering
Partitioning algorithms are clustering techniques that subdivide the data sets into a set of k groups, where k is the number of groups pre-specified by the analyst.
There are different types of partitioning clustering methods. The most popular is the K-means clustering (MacQueen 1967), in which, each cluster is represented by the center or means of the data points belonging to the cluster. The K-means method is sensitive to outliers.
An alternative to k-means clustering is the K-medoids clustering or PAM (Partitioning Around Medoids, Kaufman & Rousseeuw, 1990), which is less sensitive to outliers compared to k-means.
Read more: Partitioning Clustering methods.
The following R codes show how to determine the optimal number of clusters and how to compute k-means and PAM clustering in R.
- Determining the optimal number of clusters: use
factoextra::fviz_nbclust()
library("factoextra")
fviz_nbclust(my_data, kmeans, method = "gap_stat")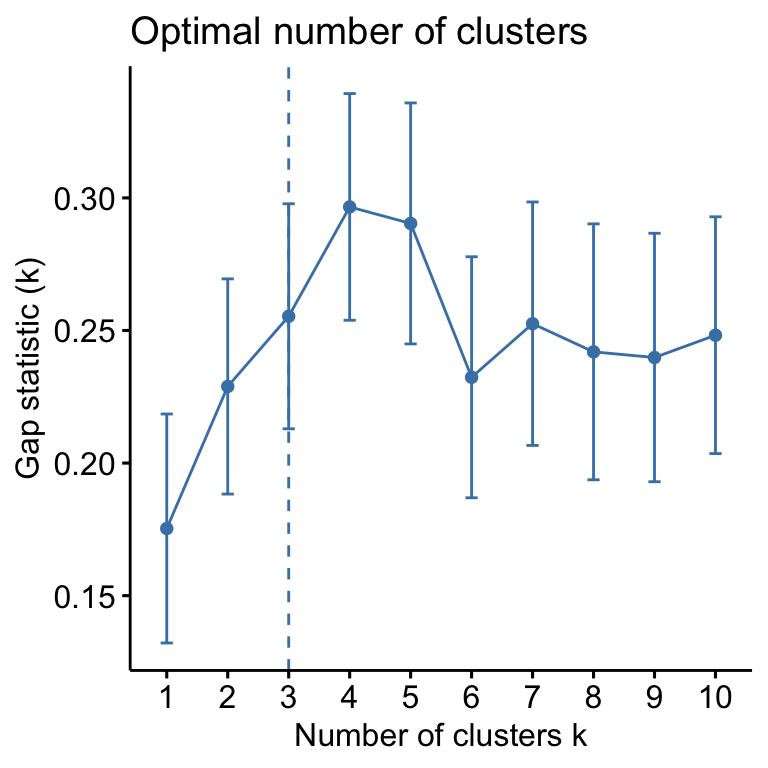
Suggested number of cluster: 3
Compute and visualize k-means clustering
set.seed(123)
km.res <- kmeans(my_data, 3, nstart = 25)
# Visualize
library("factoextra")
fviz_cluster(km.res, data = my_data,
ellipse.type = "convex",
palette = "jco",
ggtheme = theme_minimal())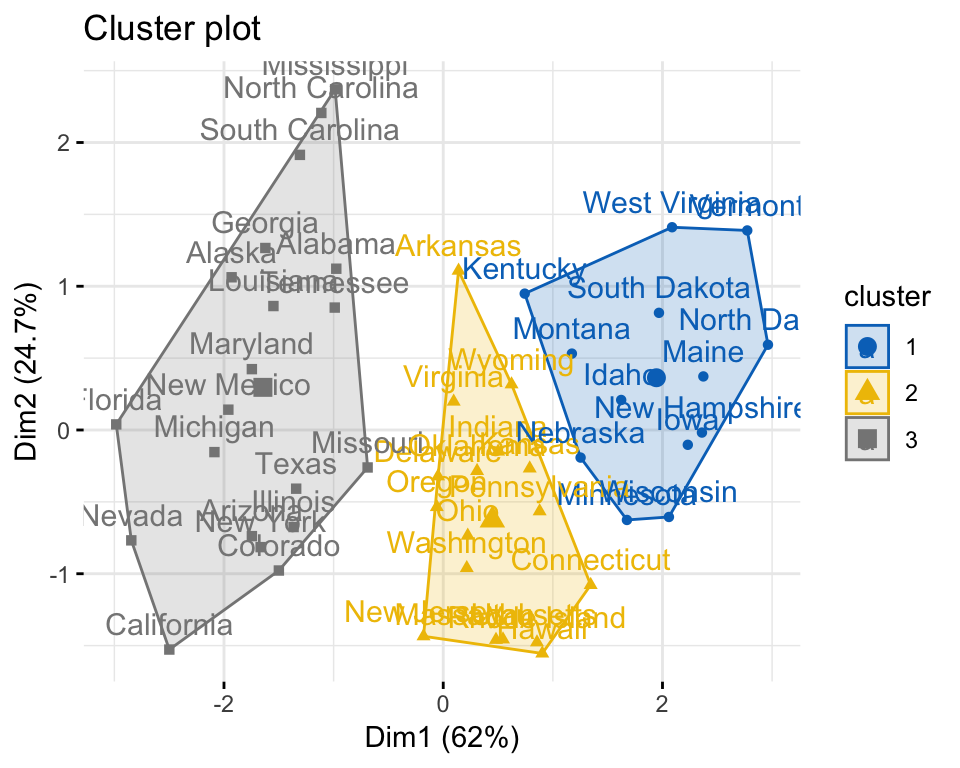
Similarly, the k-medoids/pam clustering can be computed as follow:
# Compute PAM
library("cluster")
pam.res <- pam(my_data, 3)
# Visualize
fviz_cluster(pam.res)Hierarchical clustering
Hierarchical clustering is an alternative approach to partitioning clustering for identifying groups in the dataset. It does not require to pre-specify the number of clusters to be generated.
The result of hierarchical clustering is a tree-based representation of the objects, which is also known as dendrogram. Observations can be subdivided into groups by cutting the dendrogram at a desired similarity level.
R code to compute and visualize hierarchical clustering:
# Compute hierarchical clustering
res.hc <- USArrests %>%
scale() %>% # Scale the data
dist(method = "euclidean") %>% # Compute dissimilarity matrix
hclust(method = "ward.D2") # Compute hierachical clustering
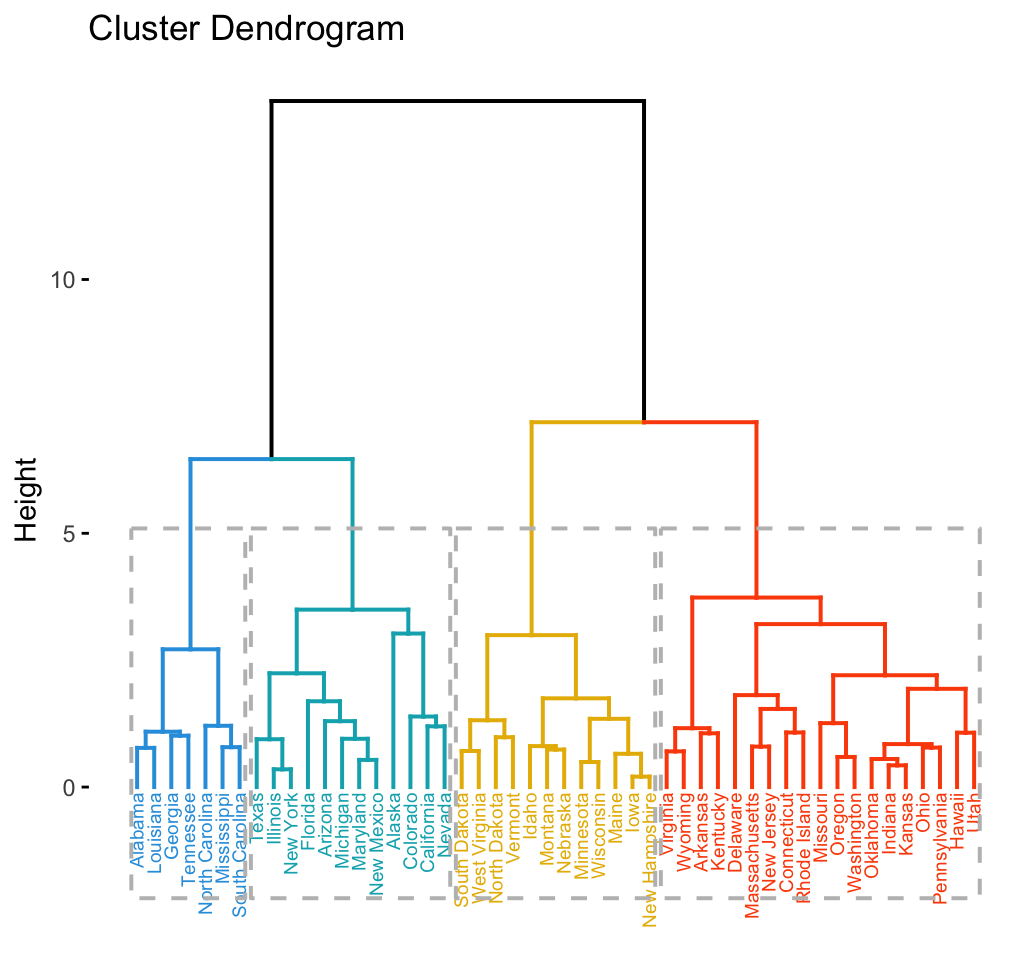
# Visualize using factoextra
# Cut in 4 groups and color by groups
fviz_dend(res.hc, k = 4, # Cut in four groups
cex = 0.5, # label size
k_colors = c("#2E9FDF", "#00AFBB", "#E7B800", "#FC4E07"),
color_labels_by_k = TRUE, # color labels by groups
rect = TRUE # Add rectangle around groups
)
Read more: Hierarchical clustering
See also:
Clustering validation and evaluation
Clustering validation and evaluation strategies, consist of measuring the goodness of clustering results. Before applying any clustering algorithm to a data set, the first thing to do is to assess the clustering tendency. That is, whether the data contains any inherent grouping structure.
If yes, then how many clusters are there. Next, you can perform hierarchical clustering or partitioning clustering (with a pre-specified number of clusters). Finally, you can use a number of measures, described in this chapter, to evaluate the goodness of the clustering results.
Read more: Cluster Validation Essentials
Assessing clustering tendency
To assess the clustering tendency, the Hopkins’ statistic and a visual approach can be used. This can be performed using the function get_clust_tendency() [factoextra package], which creates an ordered dissimilarity image (ODI).
- Hopkins statistic: If the value of Hopkins statistic is close to 1 (far above 0.5), then we can conclude that the dataset is significantly clusterable.
- Visual approach: The visual approach detects the clustering tendency by counting the number of square shaped dark (or colored) blocks along the diagonal in the ordered dissimilarity image.
R code:
gradient.color <- list(low = "steelblue", high = "white")
iris[, -5] %>% # Remove column 5 (Species)
scale() %>% # Scale variables
get_clust_tendency(n = 50, gradient = gradient.color)## $hopkins_stat
## [1] 0.8
##
## $plot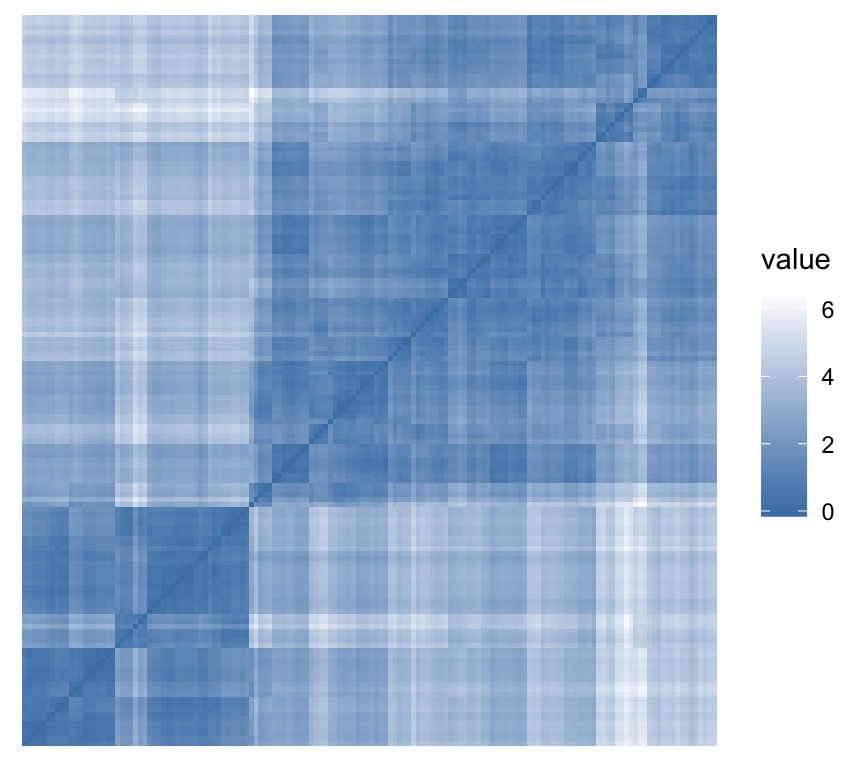
Read more: Assessing Clustering Tendency
Determining the optimal number of clusters
There are different methods for determining the optimal number of clusters.
In the R code below, we’ll use the NbClust R package, which provides 30 indices for determining the best number of clusters. First, install it using install.packages("NbClust"), then type this:
set.seed(123)
# Compute
library("NbClust")
res.nbclust <- USArrests %>%
scale() %>%
NbClust(distance = "euclidean",
min.nc = 2, max.nc = 10,
method = "complete", index ="all") # Visualize
library(factoextra)
fviz_nbclust(res.nbclust, ggtheme = theme_minimal())## Among all indices:
## ===================
## * 2 proposed 0 as the best number of clusters
## * 1 proposed 1 as the best number of clusters
## * 9 proposed 2 as the best number of clusters
## * 4 proposed 3 as the best number of clusters
## * 6 proposed 4 as the best number of clusters
## * 2 proposed 5 as the best number of clusters
## * 1 proposed 8 as the best number of clusters
## * 1 proposed 10 as the best number of clusters
##
## Conclusion
## =========================
## * According to the majority rule, the best number of clusters is 2 .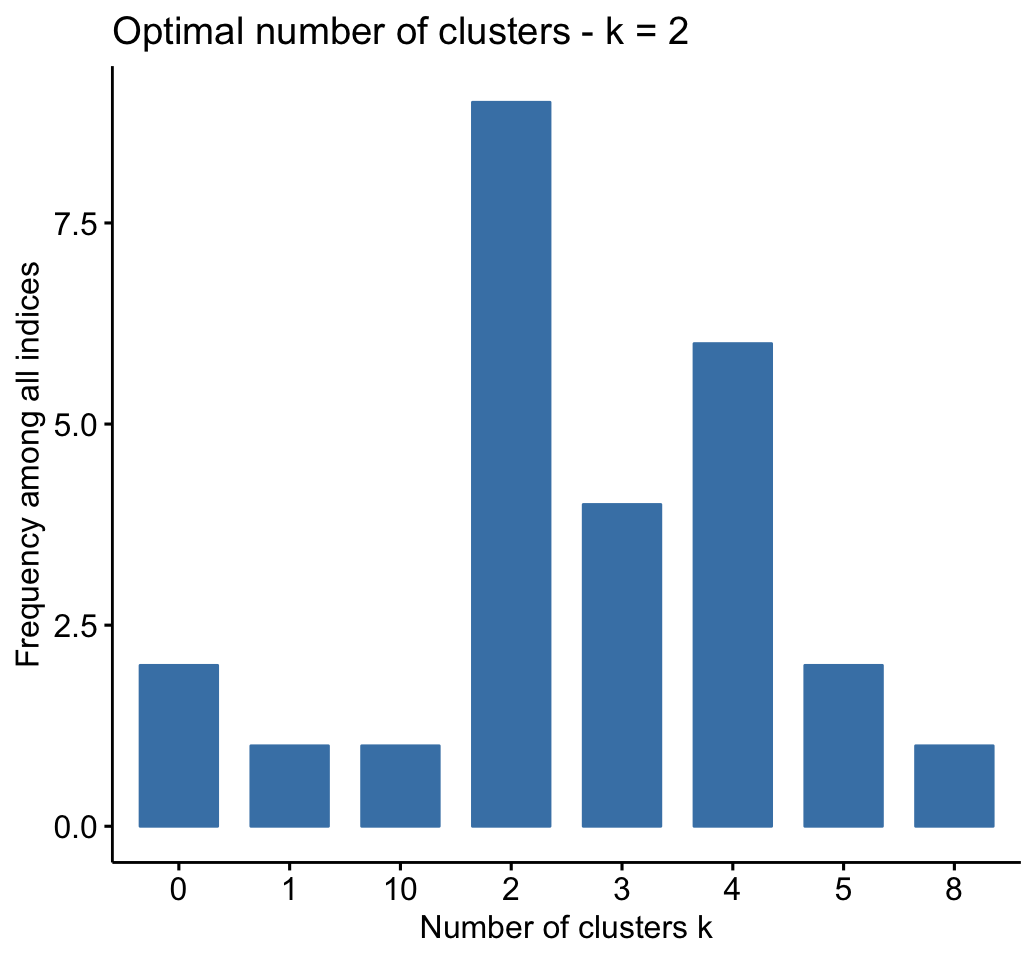
Read more: Determining the Optimal Number of Clusters
Clustering validation statistics
A variety of measures has been proposed in the literature for evaluating clustering results. The term clustering validation is used to design the procedure of evaluating the results of a clustering algorithm.
The silhouette plot is one of the many measures for inspecting and validating clustering results. Recall that the silhouette (\(S_i\)) measures how similar an object \(i\) is to the the other objects in its own cluster versus those in the neighbor cluster. \(S_i\) values range from 1 to - 1:
- A value of \(S_i\) close to 1 indicates that the object is well clustered. In the other words, the object \(i\) is similar to the other objects in its group.
- A value of \(S_i\) close to -1 indicates that the object is poorly clustered, and that assignment to some other cluster would probably improve the overall results.
In the following R code, we’ll compute and evaluate the result of hierarchical clustering methods.
- Compute and visualize hierarchical clustering:
set.seed(123)
# Enhanced hierarchical clustering, cut in 3 groups
res.hc <- iris[, -5] %>%
scale() %>%
eclust("hclust", k = 3, graph = FALSE)
# Visualize with factoextra
fviz_dend(res.hc, palette = "jco",
rect = TRUE, show_labels = FALSE)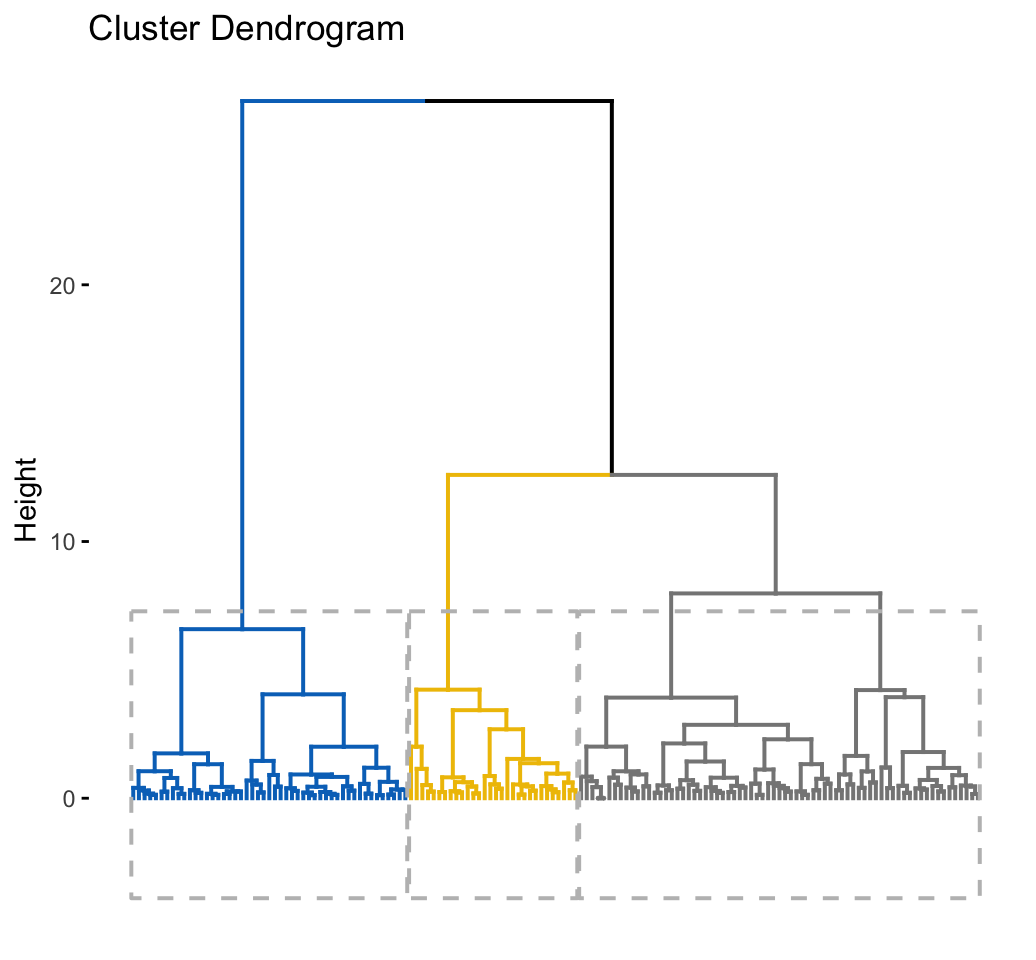
- Inspect the silhouette plot:
fviz_silhouette(res.hc)## cluster size ave.sil.width
## 1 1 49 0.63
## 2 2 30 0.44
## 3 3 71 0.32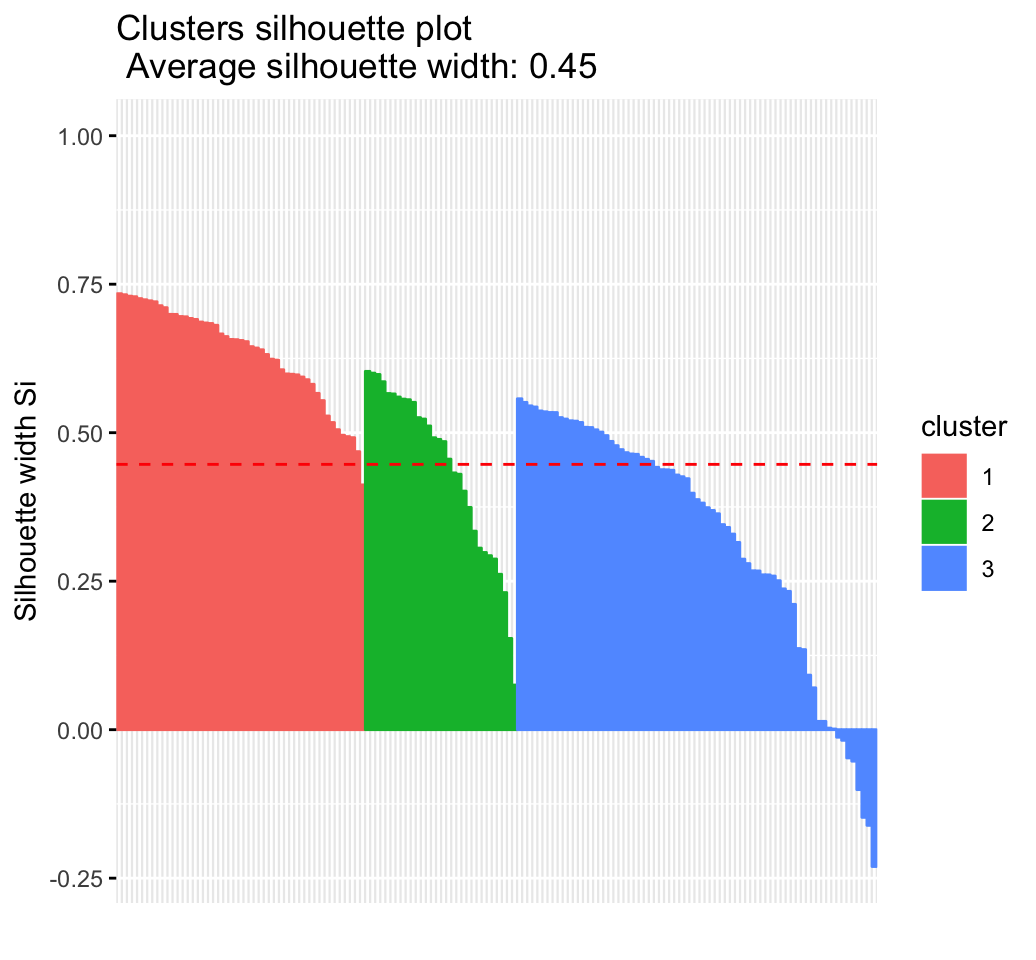
- Which samples have negative silhouette? To what cluster are they closer?
# Silhouette width of observations
sil <- res.hc$silinfo$widths[, 1:3]
# Objects with negative silhouette
neg_sil_index <- which(sil[, 'sil_width'] < 0)
sil[neg_sil_index, , drop = FALSE]## cluster neighbor sil_width
## 84 3 2 -0.0127
## 122 3 2 -0.0179
## 62 3 2 -0.0476
## 135 3 2 -0.0530
## 73 3 2 -0.1009
## 74 3 2 -0.1476
## 114 3 2 -0.1611
## 72 3 2 -0.2304Read more: Cluster Validation Statistics
Advanced clustering methods
Hybrid clustering methods
- Hierarchical K-means Clustering: an hybrid approach for improving k-means results
- HCPC: Hierarchical clustering on principal components
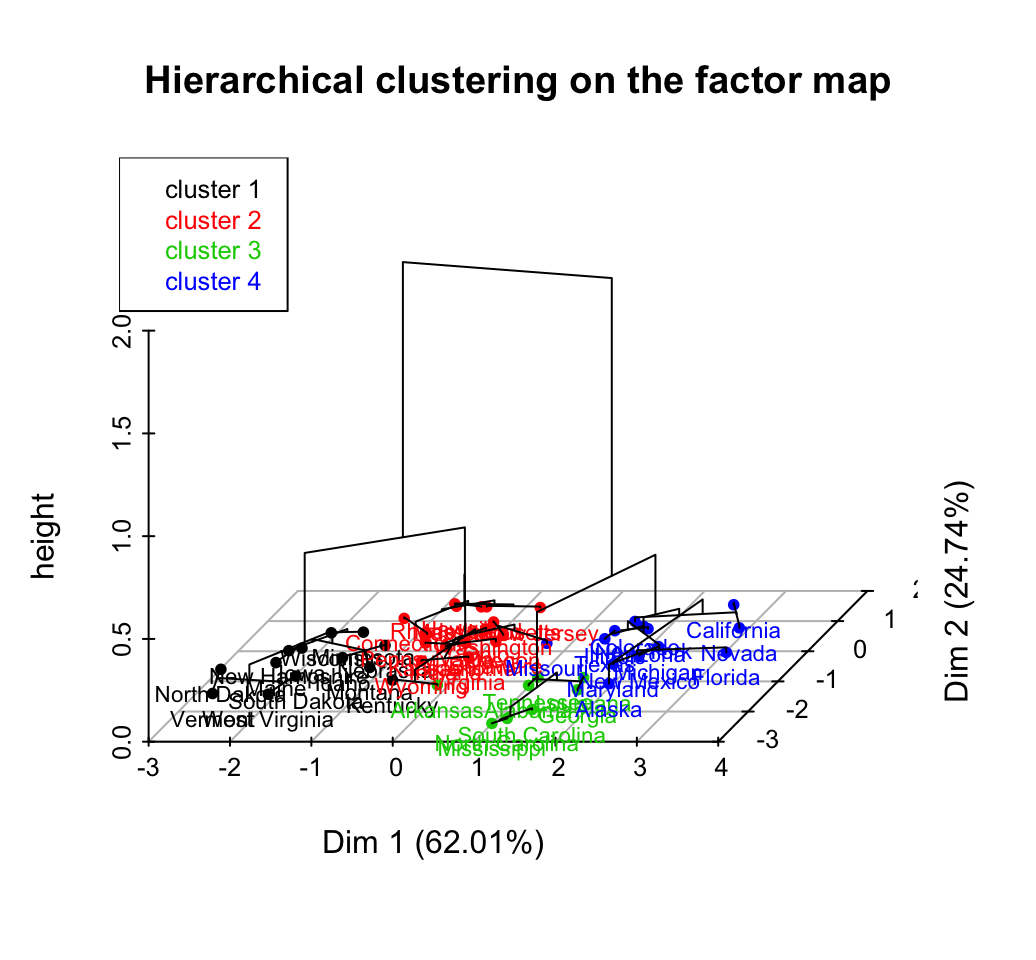
Fuzzy clustering
Fuzzy clustering is also known as soft method. Standard clustering approaches produce partitions (K-means, PAM), in which each observation belongs to only one cluster. This is known as hard clustering.
In Fuzzy clustering, items can be a member of more than one cluster. Each item has a set of membership coefficients corresponding to the degree of being in a given cluster. The Fuzzy c-means method is the most popular fuzzy clustering algorithm.
Read more: Fuzzy Clustering.
Model-based clustering
In model-based clustering, the data are viewed as coming from a distribution that is mixture of two ore more clusters. It finds best fit of models to data and estimates the number of clusters.
Read more: Model-Based Clustering.
DBSCAN: Density-based clustering
DBSCAN is a partitioning method that has been introduced in Ester et al. (1996). It can find out clusters of different shapes and sizes from data containing noise and outliers (Ester et al. 1996). The basic idea behind density-based clustering approach is derived from a human intuitive clustering method.
The description and implementation of DBSCAN in R are provided at this link: DBSCAN: Density-Based Clustering.
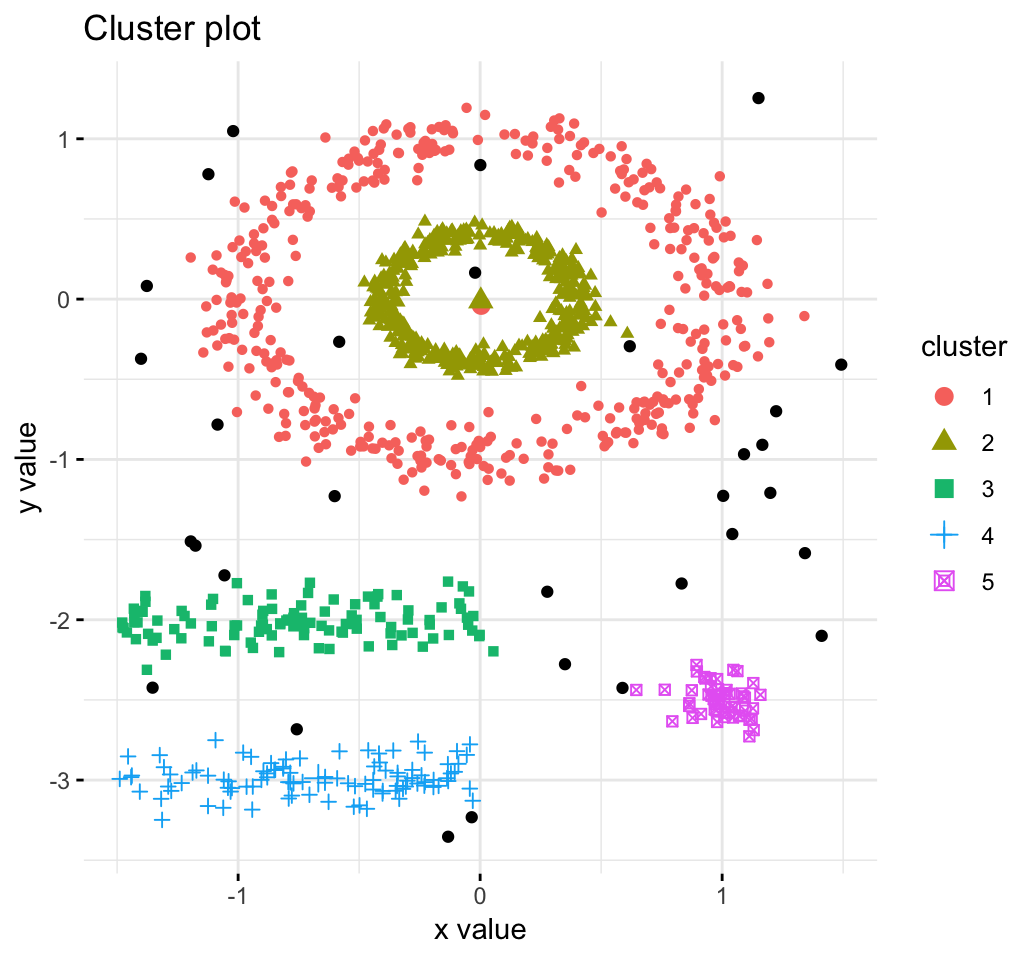
References
Ester, Martin, Hans-Peter Kriegel, Jörg Sander, and Xiaowei Xu. 1996. “A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise.” In, 226–31. AAAI Press.
MacQueen, J. 1967. “Some Methods for Classification and Analysis of Multivariate Observations.” In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics, 281–97. Berkeley, Calif.: University of California Press. http://projecteuclid.org:443/euclid.bsmsp/1200512992.
Recommended for you
This section contains best data science and self-development resources to help you on your path.
Coursera - Online Courses and Specialization
Data science
- Course: Machine Learning: Master the Fundamentals by Stanford
- Specialization: Data Science by Johns Hopkins University
- Specialization: Python for Everybody by University of Michigan
- Courses: Build Skills for a Top Job in any Industry by Coursera
- Specialization: Master Machine Learning Fundamentals by University of Washington
- Specialization: Statistics with R by Duke University
- Specialization: Software Development in R by Johns Hopkins University
- Specialization: Genomic Data Science by Johns Hopkins University
Popular Courses Launched in 2020
- Google IT Automation with Python by Google
- AI for Medicine by deeplearning.ai
- Epidemiology in Public Health Practice by Johns Hopkins University
- AWS Fundamentals by Amazon Web Services
Trending Courses
- The Science of Well-Being by Yale University
- Google IT Support Professional by Google
- Python for Everybody by University of Michigan
- IBM Data Science Professional Certificate by IBM
- Business Foundations by University of Pennsylvania
- Introduction to Psychology by Yale University
- Excel Skills for Business by Macquarie University
- Psychological First Aid by Johns Hopkins University
- Graphic Design by Cal Arts
Amazon FBA
Amazing Selling Machine
Books - Data Science
Our Books
- Practical Guide to Cluster Analysis in R by A. Kassambara (Datanovia)
- Practical Guide To Principal Component Methods in R by A. Kassambara (Datanovia)
- Machine Learning Essentials: Practical Guide in R by A. Kassambara (Datanovia)
- R Graphics Essentials for Great Data Visualization by A. Kassambara (Datanovia)
- GGPlot2 Essentials for Great Data Visualization in R by A. Kassambara (Datanovia)
- Network Analysis and Visualization in R by A. Kassambara (Datanovia)
- Practical Statistics in R for Comparing Groups: Numerical Variables by A. Kassambara (Datanovia)
- Inter-Rater Reliability Essentials: Practical Guide in R by A. Kassambara (Datanovia)
Others
- R for Data Science: Import, Tidy, Transform, Visualize, and Model Data by Hadley Wickham & Garrett Grolemund
- Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems by Aurelien Géron
- Practical Statistics for Data Scientists: 50 Essential Concepts by Peter Bruce & Andrew Bruce
- Hands-On Programming with R: Write Your Own Functions And Simulations by Garrett Grolemund & Hadley Wickham
- An Introduction to Statistical Learning: with Applications in R by Gareth James et al.
- Deep Learning with R by François Chollet & J.J. Allaire
- Deep Learning with Python by François Chollet







Thank you for sharing.
İn the silihoulette result, how can we interpret that? is the change of the datas location to the similer cluster enough for clustering validation or is that more complex than that? thankyou by the way i like the text.
Impressive blog, for anyone who wants some knowledge about clustering methods this blog is of great help. Thank you for sharing data analysis
Super informative.
I’ve really gained a lot from this.